钉钉时期的卑微努力
T1：
1.公约数
(gcd.cppcpas)
【问题描述】
给定一个正整数，在[1,n]的范围内，求出有多少个无序数对(a,b)满足
gcd(a,b)=a xor b。
【输入格式】
输入共一行，一个正整数n。
【输出格式】
输出共一行，一个正整数表示答案。
【输入输出样例】
gcd.in
gcd.out
3
1
解释：只有(2,3)满足要求
【数据范围】
对于30%的数据满足n<=1000
对于60%的数据满足n<=10^5
对于100%的数据满足n<=10^7
我们设c=a-b
也就是c为a和b的差。
想想一下，易知：当a=b时，gcd(a,b)=a xor b恒不成立。因为此时a xor b=0
又因为gcd（a,b）<=c,a xor b>=c;
则只有当gcd(a,b)=a xor b=c;时，题目中条件成立。
又可以得：gcd（a xor c,c）=c,其中c必为a的约数。
则我们可以用i*c的形式，把a表示出来。
a=i*c；
带入得：
a xor c=a-c
我们因此也得出了判断条件。
code：
#include<iostream> #include<cstdio> #include<cstring> using namespace std; int read() { int ans=0; char ch=getchar(),last=' '; while(ch>'9'||ch<'0')last=ch,ch=getchar(); while(ch<='9'&&ch>='0')ans=(ans<<3)+(ans<<1)+ch-'0',ch=getchar(); return last=='-'?-ans:ans; } int n; long long ans; int main(){ freopen("gcd.in","r",stdin); freopen("gcd.out","w",stdout); n=read(); for(int i=1;i<=n;i++) for(int j=2;j<=n/i;j++) { int a=i*j; if((a-i)==(a^i))ans++; } printf("%lld",ans); }
T2：
2.通讯
(message.cppcpas)
【问题描述】“这一切都是命运石之门的
选择。”
试图研制时间机器的机关 SERN 截获了中二科学家伦太郎发往过去的一条
短信，并由此得知了伦太郎制作出了电话微波炉（仮）。
为了掌握时间机器的技术，SERN 总部必须尽快将这个消息通过地下秘密通讯
网络，传达到所有分部。
SERN 共有 N 个部门（总部编号为 0），通讯网络有 M 条单向通讯线路，每条
线路有一个固定的通讯花费 Ci。
为了保密，消息的传递只能按照固定的方式进行：从一个已知消息的部门向
另一个与它有线路的部门传递（可能存在多条通信线路）。我们定义总费用为所
有部门传递消息的费用和。
幸运的是，如果两个部门可以直接或间接地相互传递消息（即能按照上述方法
将信息由 X 传递到 Y，同时能由 Y 传递到 X），我们就可以忽略它们之间的花费。
由于资金问题（预算都花在粒子对撞机上了），SERN 总部的工程师希望知道，
达到目标的最小花费是多少。
【输入格式】多组数据，文件以 2
个 0 结尾。
每组数据第一行，一个整数 N，表示有 N 个包括总部的部门（从 0 开始编号）。
然后是一个整数 M，表示有 M 条单向通讯线路。
接下来 M 行，每行三个整数,Xi,Yi,Ci，表示第 i 条线路从 Xi 连向 Yi，花费
为
Ci。
【输出格式】
每组数据一行，一个整数表示达到目标的最小花费。
【输入输出样例】
message.in
message.out
3 3
150
0 1 100
100
1 2 50
50
0 2 100
3 3
0 1 100
1 2 50
2 1 100
2 2
0 1 50
0 1 100
0 0【样例解释】第一组数据：总部把消息传给分部 1，分部 1 再传给分
部 2.总费用：
100+50=150.
第二组数据：总部把消息传给分部 1，由于分部 1 和分部 2 可以互相传递消
息，所以分部 1 可以无费用把消息传给 2.总费用：100+0=100.
第三组数据：总部把消息传给分部 1，最小费用为 50.总费用：50.
【数据范围】对于 10%的数据，
保证 M=N-1
对于另 30%的数据，N ≤ 20 ，M ≤ 20 对于 100%的数据，N ≤ 50000 ，
M ≤ 10^5 ，Ci ≤ 10^5 ，数据组数 ≤ 5
数据保证一定可以将信息传递到所有部门。
题目解读：
N个点，M条有向边，每条边边权ci，同一个强连通分量里相互到达的点可以忽略途径边边权。求两点之间传递所需费用总和。
关键点是要把“如果两个部门可以直接或间接地相互传递消息（即能按照上述方法将信息由 X 传递到 Y，同时能由 Y 传递到 X），我们就可以忽略它们之间的花费”这一句话翻译成“同一个强连通分量里相互到达的点可以忽略途径边边权”，那么剩下的需要费用的就是连接不同的强联通分量里的边的边权和了。
跑tarjan，统计。
#include<iostream> #include<cstdio> #include<cstring> #define N 50001 #define M 100001 #define ll long long using namespace std; int n,m; int dfn[N],low[N],dep=0,top=0,st[N],to[M],next[M],head[M],dis[M],num=0,c[N],tot=0,f[N]; bool judge[N]; int read() { int ans=0; char ch=getchar(),last=' '; while(ch>'9'||ch<'0')last=ch,ch=getchar(); while(ch<='9'&&ch>='0')ans=(ans<<3)+(ans<<1)+ch-'0',ch=getchar(); return last=='-'?-ans:ans; } void link(int x,int y,int c) { num++; to[num]=y; next[num]=head[x]; head[x]=num; dis[num]=c; } void tarjan(int x) { low[x]=dfn[x]=++dep; st[++top]=x; judge[x]=true; for(int i=head[x];i;i=next[i]) { int v=to[i]; if(!dfn[v]) { tarjan(v); low[x]=min(low[x],low[v]); } else if(judge[v]) low[x]=min(low[x],dfn[v]); } if(low[x]==dfn[x]) { tot++; while(st[top+1]!=x&&top) { c[st[top]]=tot; judge[st[top]]=0; top--; } } } int main() { freopen("message.in","r",stdin); freopen("message.out","w",stdout); n=read(),m=read(); while(n!=0&&m!=0) { memset(head,0,sizeof(head));memset(next,0,sizeof(next));memset(to,0,sizeof(to));memset(dis,0,sizeof(dis)); num=0; for(int i=1;i<=m;i++) { int u,v,w; u=read(),v=read(),w=read(); link(u,v,w); } dep=top=tot=0;memset(judge,0,sizeof(judge));memset(dfn,0,sizeof(dfn));memset(low,0,sizeof(low));memset(c,0,sizeof(c));memset(st,0,sizeof(st)); tarjan(0); ll ans=0; memset(f,60,sizeof(f)); for(int i=0;i<=n-1;i++) for(int j=head[i];j;j=next[j]) { int v=to[j]; if(c[i]!=c[v]) f[c[v]]=min(f[c[v]],dis[j]); } for(int i=1;i<=tot-1;i++) if(i!=c[0]) ans+=f[i]; printf("%lld ",ans); n=read(),m=read(); } return 0; }
T3：
div>
3．label
(label.cpp/c/pas)
【问题描述】
Samjia和Peter不同，他喜欢玩树。所以Peter送给他一颗大小为n的树，节
点编号从1到n。
Samjia要给树上的每一个节点赋一个[1,m]之间的权值，并使得有边直接相
连的两个节点的权值之差的绝对值 ≥ k。请你告诉Samjia有多少种不同的赋值
方案，只用求出答案对109+7(1000000007)取模得到的结果。
【输入格式】
输入文件名为 label.in。
输入数据的第一行包含一个整数 T，代表测试数据组数。
接下来是 T 组数据.
每组数据的第一行包含三个整数 n、m 和 k。
接下来 n − 1 行，每行包含两个整数 u 和 v， 代表节点 u 和 v 之间有
一条树边。
【输出格式】
输出文件名为 label.out。
对于每组数据，输出一行，包含一个整数，代表所求的答案。
【输入输出样例】
label.in
label.out
3
2 2 0
1 2
3 3 2
1 3
1 2
3 3 1
1 2
2 3
4
2
12【输入输出样例说明】
对于第一组样例，满足的方案如下
图中方括号内的数字（[x]）代表给节点赋的值。
【数据规模与约定】
测试点编号
m ≤
特殊约定
1,2
100
无
3,4
10000
无
5,6
109
第2-n号节点与1号节点直接相连
7,8
109
第i号节点与第i+1号节点直接相连
9,10
109
无
对于所有数据，T≤10,n≤100,k≤100,m≤10^9
看得出来，一道树形dp。
对于20分，不难推出dp方程为：
其中，f[i][j]表示节点i权值为j的方案数，v为子树编号，从叶节点开始，赋初值为1，界定上下取值范围进行推导。时间复杂度O（nm^2）
对于40分，注意右边式子中的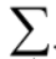
，。其中i是连续的，根据这两个特点，我们可以用前缀和来降低时间复杂度，变为O（nm）
对于满分正解，我们可以观察到一个性质：
dp值是对称的。
原因也很好理解。上下界只是一个限制，处于上界和下界的情况本质上是相同的，初始值均为1，没有任何区别。
那么在上界存在的情况，在下界也一定存在相同的情况。这就出现了对称的性质。并且中间有一段数值相等。
对于数值的情况，从叶节点往上推，每层最多增加k个不同情况，总体最多有(n-1)*k个，
那么我们可以设dp[i][j]表示i节点值为j的方案数，其中j<=(n-1)*k。
对于中间的一大段相等的，我们将其视为1种情况，这样就再次进行了优化。
上code（很不幸考试时没能打出来所以这是std）：
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define fo(i,a,b) for(int i=a;i<=b;i++) #define fd(i,a,b) for(int i=a;i>=b;i--) #define maxn 105 #define maxm 10005 #define mo 1000000007 #define mem(a,b) memset(a,b,sizeof(a)) #define ll long long using namespace std; int f[maxn][maxm]; int T,n,m,K,lim; int head[maxn],t[maxn * 2],next[maxn * 2],sum; void insert(int x,int y){ t[++sum]=y; next[sum]=head[x]; head[x]=sum; } ll getsum(int w,int from){ ll ret=0; fo(i,from,lim) ret=(ret+f[w][i]) % mo; fd(i,m,m-lim+1) { if (i<=lim || i<from) break; ret=(ret+f[w][m-i+1]) % mo; } int l=max(lim+1,from),r=m-lim; int tmp=r-l+1; if (tmp>0) ret=(ret+1ll*f[w][lim]*tmp%mo) % mo; return ret; } void dfs(int x,int father){ fo(i,1,lim) f[x][i]=1; for(int tmp=head[x];tmp;tmp=next[tmp]) { if (t[tmp]==father) continue; dfs(t[tmp],x); ll sum=getsum(t[tmp],K+1); fo(i,1,lim) { if (i-K>=1) sum=(sum+f[t[tmp]][i-K]) % mo; f[x][i]=sum*f[x][i] % mo; if (i+K<=m){ int pq=i+K; if (m-lim+1<=pq) pq=m-pq+1; else if (lim<=pq) pq=lim; sum=(sum-f[t[tmp]][pq]+mo) % mo; } } } } int mul(int x,int y){ int ret=1; while (y){ if (y % 2==1) ret=ret*1ll*x % mo; x=1ll*x*x % mo; y /=2 ; } return ret; } int main(){ freopen("label.in","r",stdin); freopen("label.out","w",stdout); scanf("%d",&T); while (T--) { mem(head,0); sum=0; scanf("%d%d%d",&n,&m,&K); fo(i,1,n-1) { int x,y; scanf("%d%d",&x,&y); insert(x,y); insert(y,x); } if (K==0) { int ans=mul(m,n); printf("%d ",ans); continue; } lim=min(10000,m); dfs(1,0); printf("%d ",getsum(1,1)); } return 0; }
钉钉时期，大家在家也要加油！。
完结撒花。