前言:回去刷数论的题,发现自己的高斯消元是0分。。。。。。很可能是当年交上去了没看结果就直接过了。。。。。。回来博客园搜自己之前对高斯消元的讲解想看看,没看到。只能从头过了一遍,顺便补上之前的锅。
高斯消元:
什么是高斯消元: 线性代数规划中的一个算法,可用来为线性方程组求解——度娘
在现阶段的学习中,高斯消元常被应用于求多项式的解:
形如
x+3y+2z=1,
2x+7y-z=2,
3x-2y+5z=9。
的多项式。
根据平常文化课的学习,我们不难知道对于n个未知数,只要给你n个不同(化简后依然不同)的多项式即可求出每一个未知数的解。在2元方程以下我们一般直接秒掉。3元也不是很难,再往上的就有点费精力了。高斯消元就是将多项式系数和结果抽象成一个矩阵,经过一些颠三倒四不知所以的操作后,成功求出多项式的解的过程。
举例:(借用了pksAFO巨佬的例子)
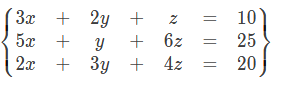
以上是三个三元方程,我们将其抽象成矩阵后,变为:
|3 2 1 10|
|5 1 6 25|
|2 3 4 20|(这个蒟蒻不会markdown?踩他)
假设有n个未知数,那么矩阵就有n行n+1列。
此矩阵的奇怪性质:
1.对于多个多项式,你把其中一个写在最上方,或者写在最下方,很明显就是换了个顺序,所以对答案并没有什么影响。也就是,矩阵的行可以任意互换。
2.小学学过的方法:对于一整行多项式,你把它整体上扩大/缩小多少倍,对答案没有影响。矩阵同一行上的数,可以任意扩大/缩小k倍(k为实数)。
3.二元方程常用方法:加减相消。具体例子:
x+2y=5; 1式
3x-2y=-1; 2式
2式+1式得:4x=4,x=1,y=2。
换句话说,我们可以这样表达:
(1+3)x+(2-2)y=5-1;
0x+0y=0;(加到1式上了,没用了)
变成这样:
4x+0y=4;
0x+0y=1;
回过来,我们可以把这两个二元多项式方程看做矩阵:
|1 2 5|
|3 -2 -1|
我们可以将第二行整体加到第一行上,使得矩阵变成了:
|4 0 4|
|0 0 0|
求得x=1,回带得y=2。
对于矩阵上任意一行,我们都可以将其整体地对于另一行进行加/减。
如何利用这三个性质进行求方程解?
灵活运用性质2和3,将矩阵除对角线以外消为0:
1 0 0 k
0 1 0 a
0 0 1 b
解就是k,a,b。
步骤:
1.把当前对角线上的元素运用性质2变成1
2.用这个1去消掉除了当前对角线上的元素
重复这两个步骤n次(对角线长度)
注意:在对角线元素变为1的过程中,同一行的其他元素也要进行扩大/缩小相同的倍数。
如果1列上没有任何元素(全为0)说明这个未知数不存在,输出无解(No Solution)。
代码:
#include<iostream> #include<cstdio> #include<cmath> using namespace std; int n,mo=100000007; double a[1001][1001]; int main() { bool sc=0; scanf("%d",&n); for(int i=1;i<=n;i++) for(int j=1;j<=n+1;j++) scanf("%lf",&a[i][j]);//这次没用祖传快读doge int bj,flag=0; for(int i=1;i<=n;i++) { bj=i; while(a[bj][i]==0&&bj<=n) bj+=1; if(bj==n+1){printf("No Solution");return 0;} //以上部分,我们做的是获取第一个此列中非0的行号。如果此列全为0,证明无解,直接退出、 for(int j=1;j<=n+1;j++)swap(a[i][j],a[bj][j]); //对角线上的元素不能为0,于是我们找到当前列号不为0的一行与对角线进行交换。可能当前对角线上元素也不为0.但是这样做囊括了更多情况。 double kk=a[i][i];//确保对角线上的数是1 for(int j=1;j<=n+1;j++) a[i][j]/=kk;//其余数跟着处理,包括对角线上的数。运用性质2 for(int j=1;j<=n;j++) { if(i!=j) { double k=a[j][i]; //k=这行第一个数,因为对角线上是1,那么这个“第一个数”可以表示为1*k。所以k也就是扩大/缩小的倍数 for(int m=1;m<=n+1;m++) a[j][m]-=k*a[i][m]; //此行所有的数减去第一个数*k,运用性质2 ,3 } } if(i==n)//消完输出 { for(int j=1;j<=n;j++) printf("%.2lf ",a[j][n+1]); //只有对角线上有元素,且值为1,代表这个位置对应的列号未知数。第n+1列就代表着未知数的值。输出即可 } } }
完结撒花。希望对各位的高斯消元学习有所帮助。