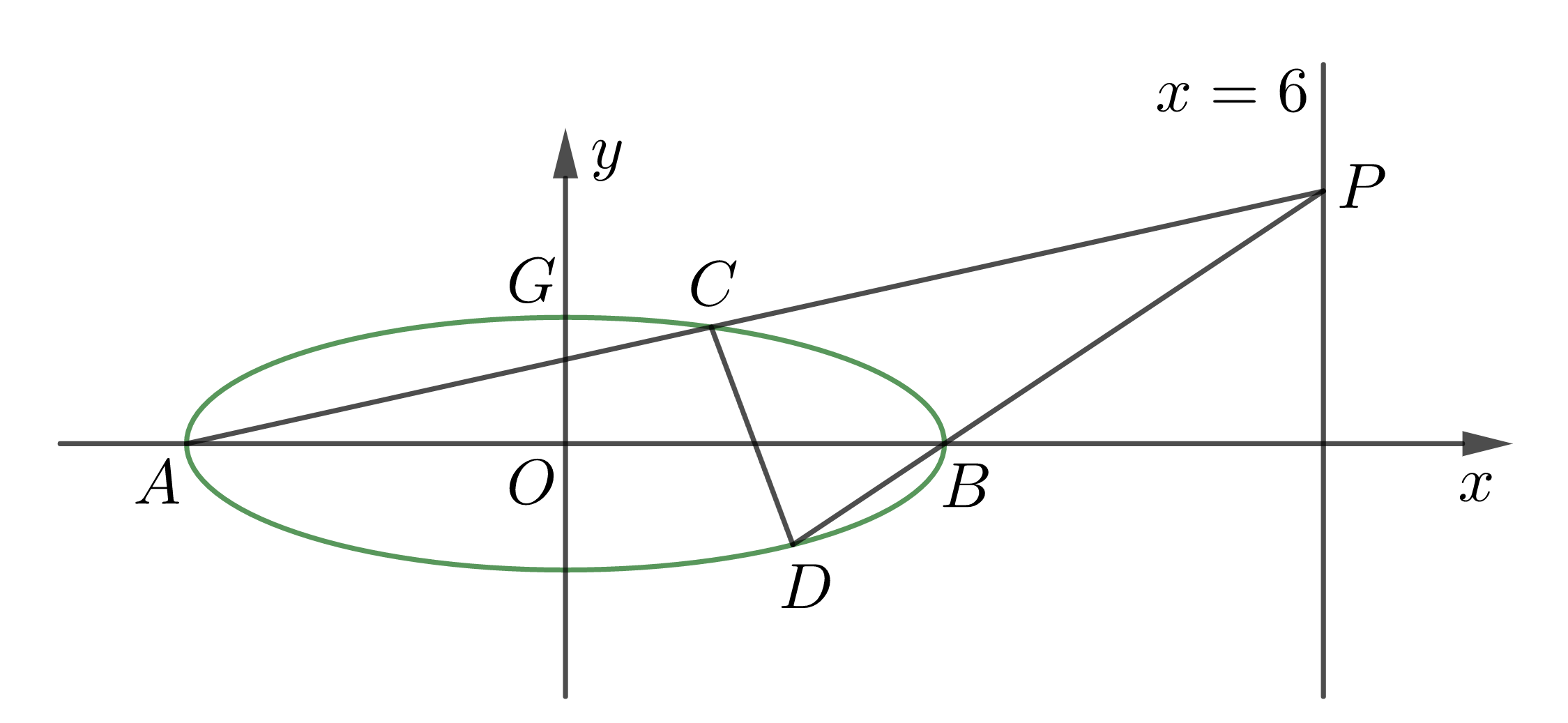
已知 (A,B) 分别为椭圆 (E:dfrac{x^2}{a^2}+y^2=1(a>0)) 的左、右顶点,(G) 为 (E) 的上顶点,(overrightarrow{AG}cdotoverrightarrow{GB}=8) ,(P) 为直线 (x=6) 上的动点,(PA) 与 (E) 的另一交点为 (C) ,(PB) 与 (E) 的另一交点为 (D) .
(1) 求 (E) 的方程;
(2) 证明:直线 (CD) 过定点.
解析:
(1) (dfrac{x^2}{9}+y^2=1)
(2) 设 (C(x_1,y_1),D(x_2,y_2)) ,则有
[l_{AC}:y=dfrac{y_1}{x_1+3}(x+3);;,;;l_{BD}:y=dfrac{y_2}{x_2-3}(x-3)
]
因为直线 (AC,BD) 交于直线 (x=6) 上同一点,则
[egin{align}dfrac{9y_1}{x_1+3}=dfrac{3y_2}{x_2-3}end{align}
]
情形一 当直线 (CD) 斜率存在时,设直线 (CD) 的方程为 (y=kx+m) ,联立
[egin{cases}y=kx+m\x^2+9y^2=9end{cases}Longrightarrow(1+9k^2)x^2+18kmx+9m^2-9=0
]
则 (x_1+x_2=-dfrac{18km}{1+9k^2},x_1x_2=dfrac{9m^2-9}{1+9k^2}) ,将 ((1)) 式两边平方得
[egin{align}dfrac{9cdot9y_1^2}{(x_1+3)^2}=dfrac{9y_2^2}{(x_2-3)^2}end{align}
]
因为 (C,D) 在椭圆 (E) 上,则
[9y_1^2=9-x_1^2;,;9y_2^2=9-x_2^2
]
代入 ((2)) 式,得
[dfrac{9cdot(9-x_1^2)}{(x_1+3)^2}=dfrac{9-x_2^2}{(x_2-3)^2}
]
化简得
[4x_1x_2-15(x_1+x_2)+36=0
]
则
[4cdotdfrac{9m^2-9}{1+9k^2}+15cdotdfrac{18km}{1+9k^2}+36=0
]
化简得
[2m^2+15km+18k^2=(2m+3k)(m+6k)=0
]
解得 (m=-dfrac{3}{2}k) 或 (m=-6k) (舍) ,则直线 (CD) 为 (y=kBig(x-dfrac32Big)) ,过定点 (Big(dfrac32,0Big)) .
情形二 当直线 (CD) 的斜率不存在时,设为 (x=m) ,则此时 (x_1=x_2=m,y_1=-y_2) ,代入 ((1)) 式求得 (m=dfrac{3}{2}) ,过点 (Big(dfrac32,0Big))
综上,直线 (CD) 过定点 (Big(dfrac32,0Big)) .