最短路径之弗洛伊德算法

下图左部分是一个最简单的3个顶点连通网图。

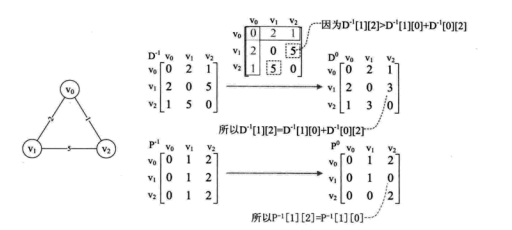
先定义两个数组D[3][3]和P[3][3]，D代表顶点到顶点的最短路径权值和的矩阵，P代表对应顶点的最小路径的前驱矩阵。在未分析任何顶点之前，我们将D命名为D^-1  ，其实它就是初始的图的邻接矩阵。将P命名为P^-1 ，初始化为图中所示的矩阵。
    首先，我们来分析，所有的顶点经过v0后到达另一顶点的最短距离。因为只有三个顶点，因此需要查看v1->v0->v2，得到D^-1 [1][0] + D^-1 [0][2] = 2 + 1 = 3。D^-1 [1][2]表示的是v1->v2的权值是5，我们发现D^-1 [1][2] > D^-1 [1][0] + D^-1 [0][2]，通俗的讲就是v1->v0->v2比直接v1->v2距离还要近。所以我们就让D^-1 [1][2]  = D^-1 [1][0] + D^-1 [0][2]，同样的D^-1 [2][1]  = 3，于是就有了D⁰ 的矩阵。因为有了变化，所以P矩阵对应的P^-1[1][2]和P^-1[2][1]也修改为当前中转的顶点v0的下标0，于是就有了P⁰。也就是说：
    --->动态规划乎
    接下来，其实也就是在D⁰和P⁰的基础上，继续处理所有顶点经过v1和v2后到达另一顶点的最短路径，得到D¹和P¹、D²和P²完成所有顶点到所有顶点的最短路径的计算。
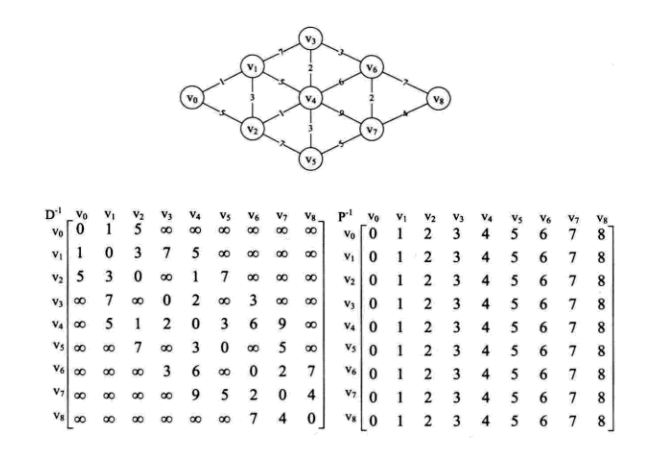
    首先我们针对下图的左网图准备两个矩阵D^-1和P^-1，就是网图的邻接矩阵，初设为P[j][j] = j这样的矩阵，它主要用来存储路径。

接下来，其实也就是在D⁰和P⁰的基础上，继续处理所有顶点经过v1和v2后到达另一顶点的最短路径，得到D¹和P¹、D²和P²完成所有顶点到所有顶点的最短路径的计算。
    首先我们针对下图的左网图准备两个矩阵D^-1和P^-1，就是网图的邻接矩阵，初设为P[j][j] = j这样的矩阵，它主要用来存储路径。

具体代码如下：

package com.neuedu.algorithm;

import java.util.ArrayList;
import java.util.List;
public class FloydInGraph {

    private static int INF = Integer.MAX_VALUE;
    private int[][] dist;
    //顶点i 到 j的最短路径长度，初值是i到j的边的权重
    private int[][] path;
    private List<Integer> result = new ArrayList<Integer>();

    public static void main(String[] args) {
        FloydInGraph graph = new FloydInGraph(5);
        int[][] matrix = {
                {INF, 30, INF, 10, 50},
                {INF, INF, 60, INF, INF},
                {INF, INF, INF, INF, INF},
                {INF, INF, INF, INF, 30},
                {50, INF, 40, INF, INF},
        };
        int begin=0;
        int end=4;
        graph.findCheapestPath(begin,end,matrix);
        List<Integer> list=graph.result;
        System.out.println(begin+" to "+end+",the cheapest path is:");
        System.out.println(list.toString());
        System.out.println(graph.dist[begin][end]);
    }

    public  void findCheapestPath(int begin,int end,int[][] matrix){
        floyd(matrix);
        result.add(begin);
        findPath(begin,end);
        result.add(end);
    }

    public void findPath(int i,int j){
        // 找到路由节点
        int k=path[i][j];
        if(k==-1)
            return;
        // 从i到路由节点进行递归寻找中间节点
        findPath(i,k);
        result.add(k);
        // 从j到路由节点进行递归寻找中间节点
        findPath(k,j);
    }
    public  void floyd(int[][] matrix){
        int size=matrix.length;
        for(int i=0;i< size;i++){
            for(int j=0;j< size;j++){
                path[i][j]=-1;
                dist[i][j]=matrix[i][j];
            }
        }
        for(int k=0;k< size;k++){
            for(int i=0;i< size;i++){
                for(int j=0;j< size;j++){
                    if(dist[i][k]!=INF&&
                        dist[k][j]!=INF&&
                        dist[i][k]+dist[k][j]< dist[i][j]){
                        // 更新i和j两点间的距离
                        dist[i][j]=dist[i][k]+dist[k][j];
                        // 更新i和j两点间的路由信息
                        path[i][j]=k;
                    }
                }
            }
        }
    }

    public FloydInGraph(int size){
        this.path=new int[size][size];
        this.dist=new int[size][size];
    }
}