20172306 2018-2019-2 《Java程序设计与数据结构》第八周学习总结
教材学习内容总结
- 堆
-
堆是具有两个附加属性的一棵二叉树
- 它是一个完全树
- 对每一结点,它小于或等于其左孩子和右孩子(这个描述的是最小堆)
- 一个堆也可以是最大堆,其中的结点大于或等于它的左右孩子
- 它继承了二叉树的所有操作

-
addElement操作
- 如果给定元素不是Comparable的,则该方法将抛出一个ClassCastException异常
- addElement方法将给定的Comparable元素添加到堆中的恰当位置处,且维持该堆的完全性属性和有序属性。
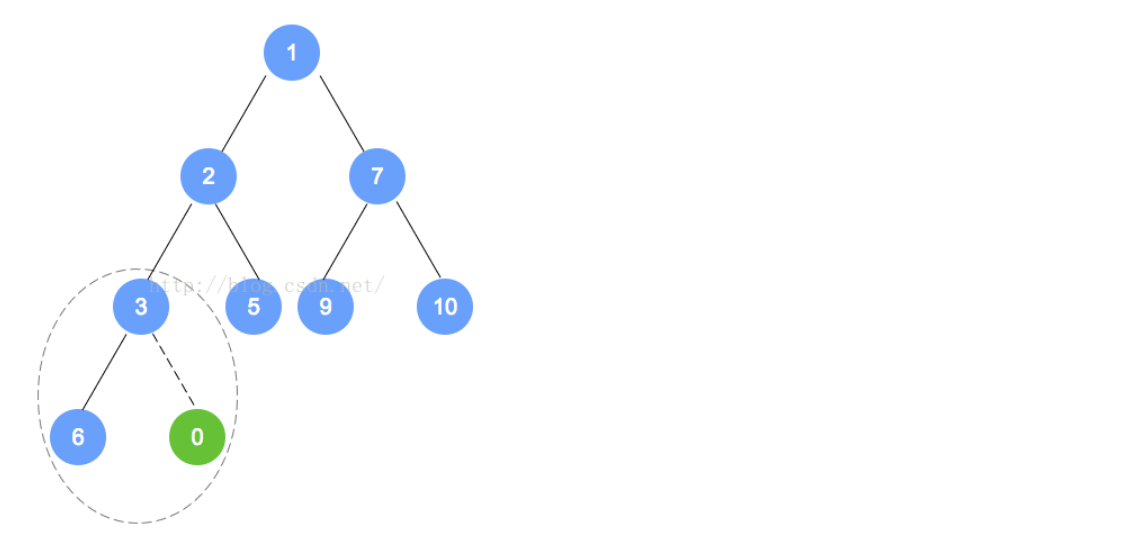
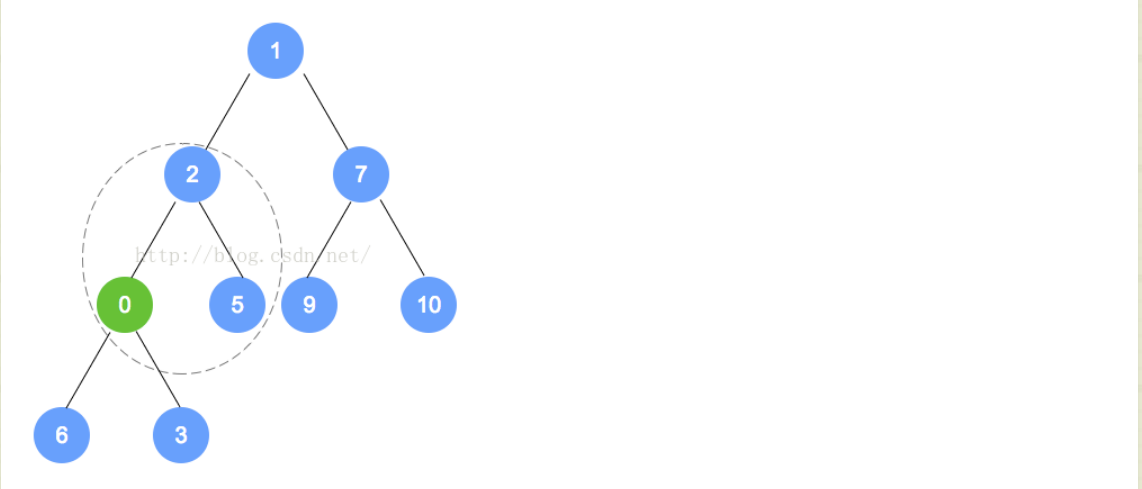
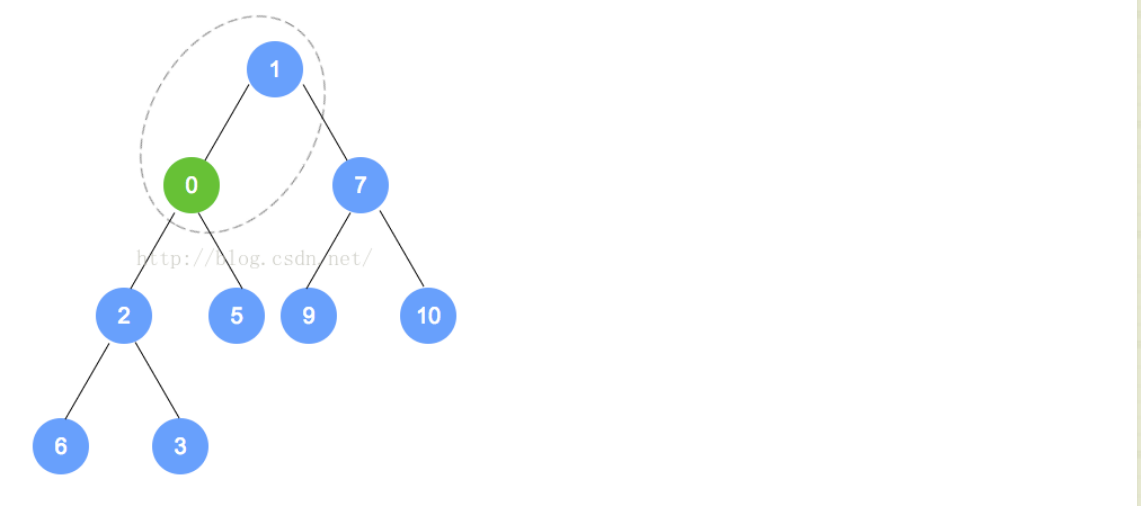
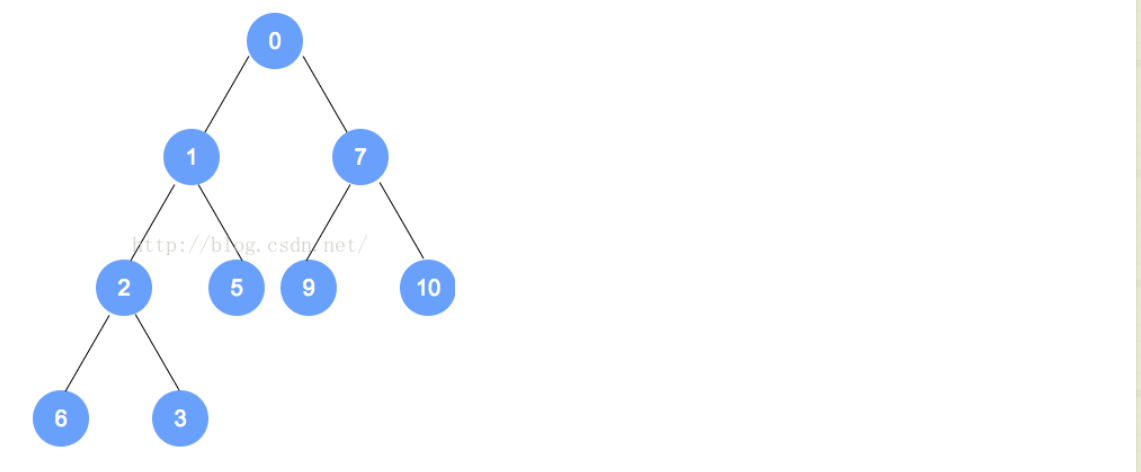
- 因为一个堆就是一棵完全树,所以对于插入的新结点而言,只存在一个正确的位置,要么就是叶子不在一层,那么就取最后一层的空处;要么就是在同一层,就在它的左面的第一个位置。在插入后,就会对它的完整性和有序性进行改变,所以就要进行重新的排序,拿该值和双亲结点进行比较,然后进行互换,然后沿着树向上继续找,直到到正确的位置。
- 通常,在堆实现中,我们会对树中的最末一个结点,或更为准确的是,最末一片叶子进行跟踪记录。
-
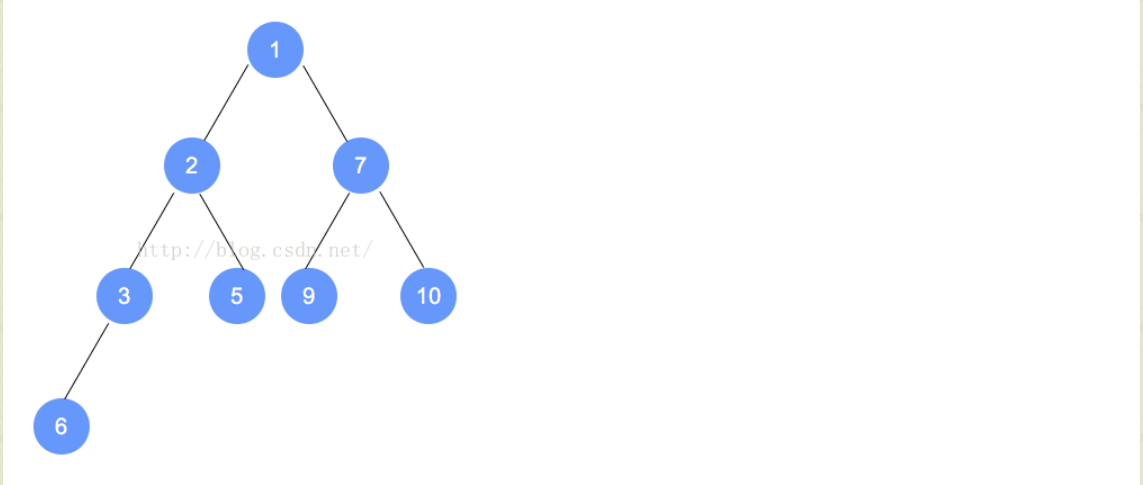
例如下面的过程(我们要插入的是0,因为插入后,不是最小堆,不符合规定,所以我们进行重排序):
-
- removeMin操作
- 对于最小堆来说,Min就是根的位置的元素。所以我们在这个方法上就是将根元素删掉,然后再进行其他操作。
- 对于这个堆来说,完整性和平衡性是很重要的,所以为了维持该树的完全性,只有一个能替换根的合法元素,且它是存储在树中最末一片叶子上的元素。对于最末一片叶子来说,就是在树最后一层最右边的叶子。
- 对于addElement来说,我们在添加的时候,有可能违背最小堆的特性,同样,对于removeMin来说,也会出现这样的问题,所以我们要进行重排序以维持其原有的属性。过程主要是将替换后的元素和它的孩子进行比较,然后依次向下,直到最后的一层,形成最小堆截止。
- 例如下面的过程:
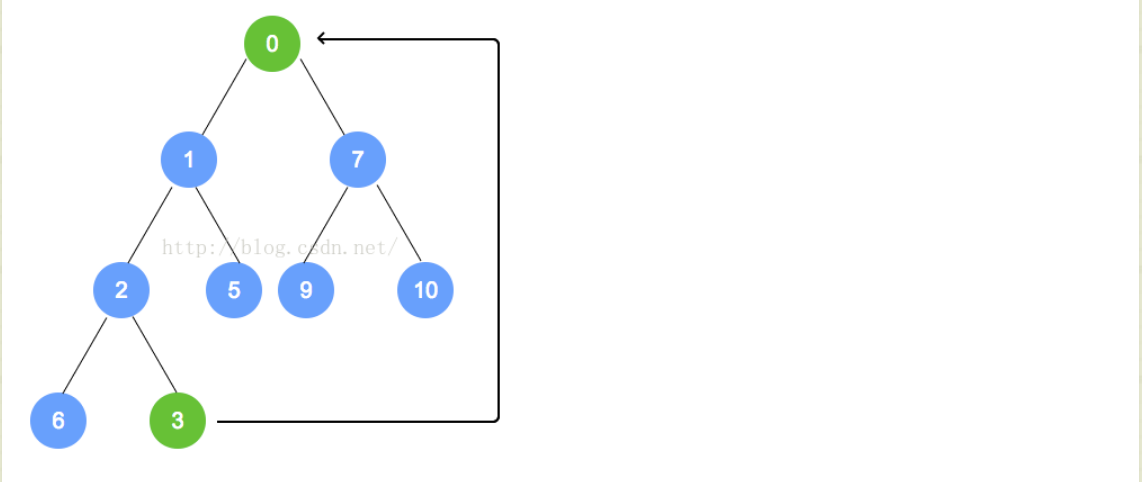
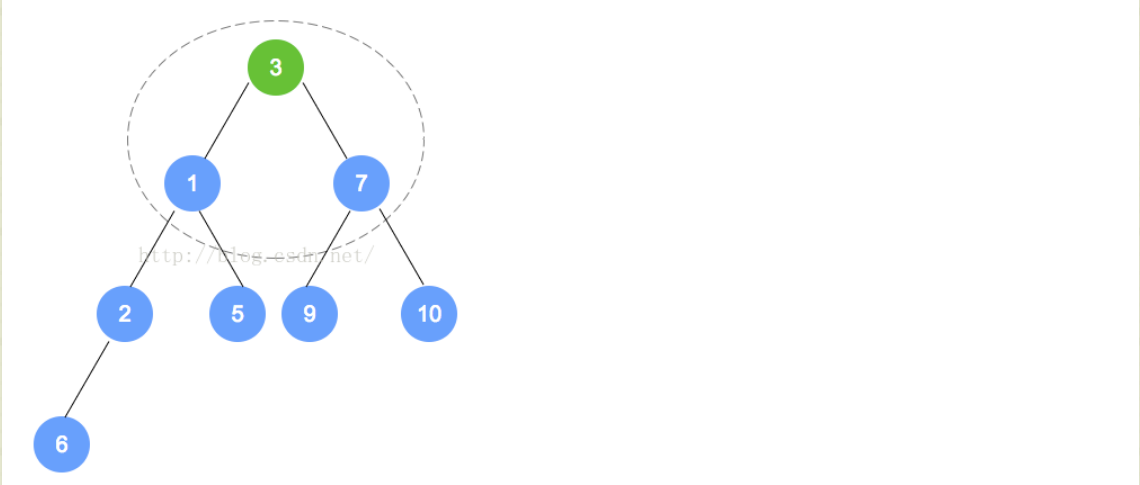
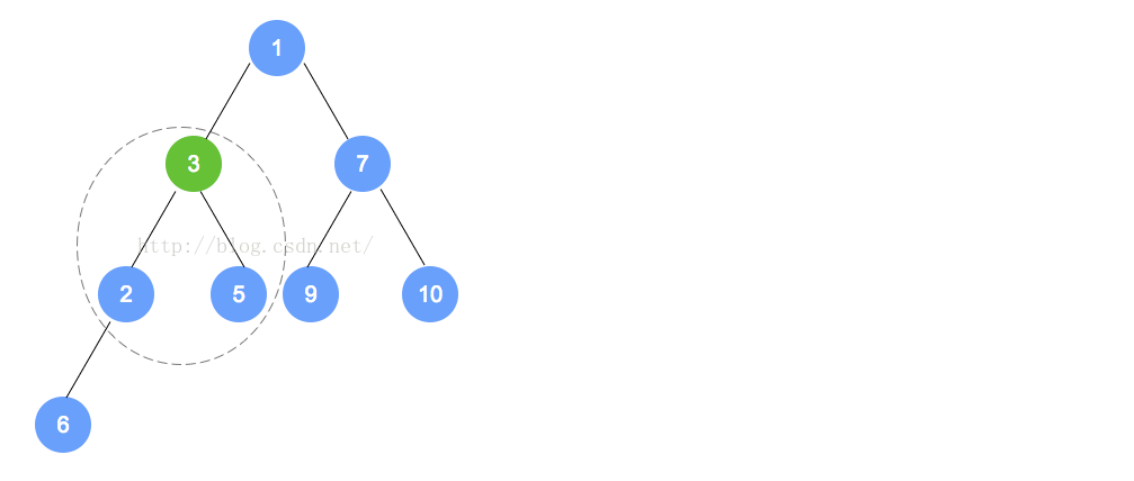
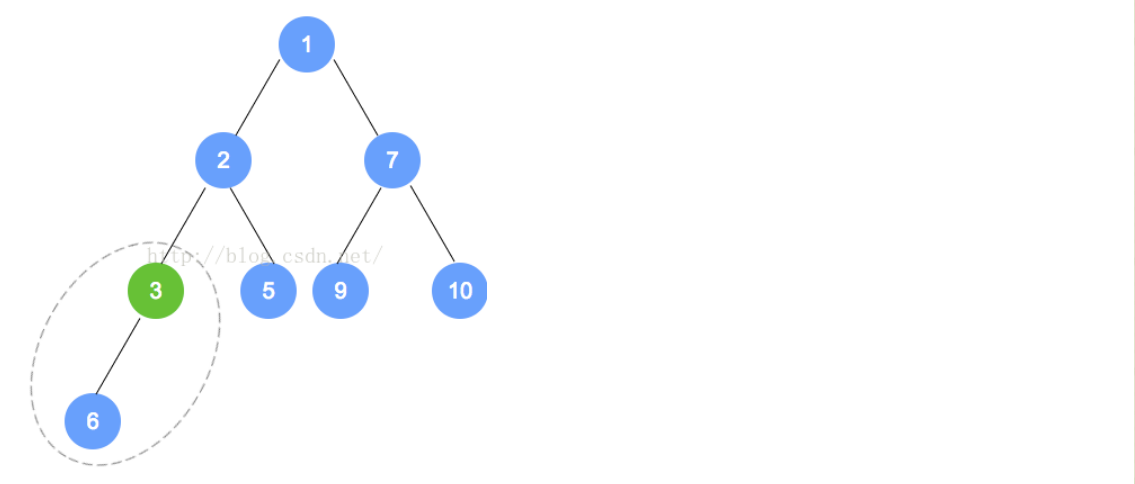
-
findMin操作
- findMin就很好理解了,因为Min就是最根部的元素,所以就将返回为root就可以了。
-
使用堆:优先级队列
- 优先级队列(priority queue):就是遵循两个排序规则的集合,首先,具有更高优先级的项目优先;其次,具有相同优先级的项目使用先进先出方法来确定其排序。
- 虽然最小堆根本不是一个队列,但是它却提供了一个高效的优先级队列实现。
- 我们利用堆来实现一个优先级队列:我们要实现以上的两个排序规则
- 首先,我们使用一个最小堆,需要将高优先级的项目在先
- 其次,我们要解决的是对相同优先级的进行先进先出的排序
- 1.创建一个PriorityQueueNode对象,存储将被放置在队列中的元素,该元素的优先级,以及元素放进队列的顺序
public PrioritizedObject(T element, int priority)
{
this.element = element;//元素
this.priority = priority;//优先级
arrivalOrder = nextOrder;//放入队列的顺序
nextOrder++;
}
- 2.为PriorityQueueNode类定义一个CompareTo方法,来完成优先级相同时的比较
public int compareTo(PrioritizedObject obj)
{
int result;
if (priority > obj.getPriority())
result = 1;
else if (priority < obj.getPriority())
result = -1;
else if (arrivalOrder > obj.getArrivalOrder())
result = 1;
else
result = -1;
return result;
}
-
链表实现和数组实现的addElement操作的时间复杂度同为o(logn)
-
链表实现和数组实现的removeMin操作的复杂度同为o(logn)
-
用链表实现堆
- 堆是二叉树的一种扩展,所以在插入元素后仍旧能够向上遍历该树,所以堆中的结点必须存储指向其双亲的指针。
- 链表实现的实例数据由指向HeapNode且称为lastNode的单个引用组成,这样我们就能够跟踪记录该堆中的最末一片叶子
public HeapNode lastNode;
-
addElement操作
- 达到3个目的:在恰当位置处添加一个新的元素;对堆进行重排序以维持排序属性;将lastNode指针重新设定为指向新的最末结点
- 其使用了两个私有方法
- getNextParentAdd:它返回一个指向某结点的引用,该结点为插入结点的双亲
- heapifyAdd:完成对堆的任何重排序,从那片新叶子开始向上处理至根处
- 添加元素对于复杂度(复杂度为:2*logn + 1 +logn,即o(logn)):
- 第一步是确定要插入结点的双亲,在最坏情况下,要从堆的右下结点往上遍历到根,然后再向下到堆的左下结点,时间复杂度为2*logn
- 下一步是插入新结点,时间复杂度为常量
- 最后一步是重排序,最多需要logn次操作
- heapifyAdd未执行双亲与孩子的完整互换,只是把双亲元素向下平移到正确的插入点,然后把新值赋给该位置。但它提高了效率,因为减少了在堆的每一层上要执行的赋值次数。
-
removeMin 操作
- 达到3个目的:用存储在最末结点处的元素替换存储在根处的元素;对堆重排序;返回初始的根元素。
- 其使用了两个私有方法
- getNewLastNode:它返回一个指向某一结点的引用,该结点是新的最末结点
- heapifyRemove:进行重排序(从根向下)
- 删除根元素对于复杂度(复杂度为:2*logn + logn + 1,即o(logn))
- 第一步是替换元素,其时间复杂度为常量
- 第二步是重排序(根往下到叶子),时间复杂度为logn
- 第三部为确定新的最末结点,和之前相同为2*logn
-
findMin操作
- 该元素在堆根处,只需返回根处即可
- 复杂度为o(1)
-
用数组实现堆
-
在二叉树的数组实现中,树的根位于位置0处,对于每一结点n,n的左孩子将位于数组的2n+1位置处,n的右孩子将位于数组的2(n+1)位置处
-
addElement操作
- 达到3个目的:在恰当位置处添加新结点;对堆进行重排序;将count递增1(我认为原因是数组是有容量的,元素增多,要给它空间)
- 其中有一个私有方法
- heapifyAdd:进行重排序
- 添加元素对于复杂度(复杂度为:1+logn,即o(logn))
- 不需要确定新结点的双亲,因为会自动根据位置进行放,但是 其他的步骤和链表相同。
- 数组实现的效率更高些,但复杂度相同为o(logn)
-
removeMin操作
- 达到3个目的:用存储在最末元素处的元素替换存储在根处的元素;对堆进行重排序;返回初始的根元素
- 其中有一个私有方法
- 最末一个元素是存储在数组的count-1位置处的(count是所有的元素值)
- heapifyRemove:进行重排序
- 删除元素对于复杂度(复杂度为:logn+1,即o(logn))
- 不需要确定新的最末结点
-
findMin操作
- 该元素为在根处,所以在数组的0位置处
- 复杂度为o(1)
-
-
使用堆:堆排序老师上课用的PPT,我觉得上面的堆排序过程很详细,而且易懂
-
heapSort方法的两部分构成:添加列表的每个元素,然后一次删除一个元素
-
就堆排序来说,老师在上课的时候讲的很详细,而且因为它是有最小堆和最大堆的,根部要不是最小元素,要不是最大元素,因此,堆排序的关键就是通过不断的移动,将最值放在根处,然后利用remove根处元素的方法,将元素删除出来,再对剩余的堆进行重排序,然后继续删除根部,而这个过程,每删除的元素排列出来就是我们所需要的升序或者降序,即堆排序完成
-
堆排序我们也可以用数组的知识进行理解。因为我们在数组实现堆时,已经知道了对于一个根结点,其左右孩子的确定所在位置,所以我们可以利用比较和互换,进行排序,其实原理和上一条是相同的。
-
无论是用列表还是数组进行堆排序,他们的复杂度相同,都是o(nlogn)
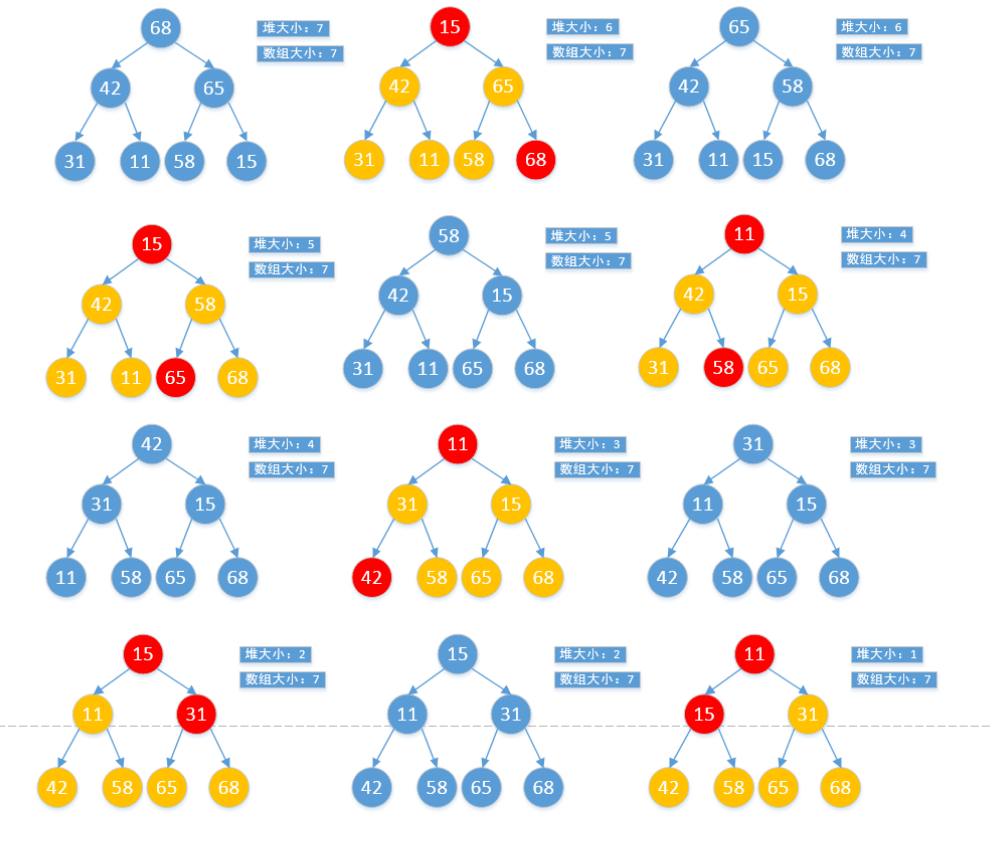
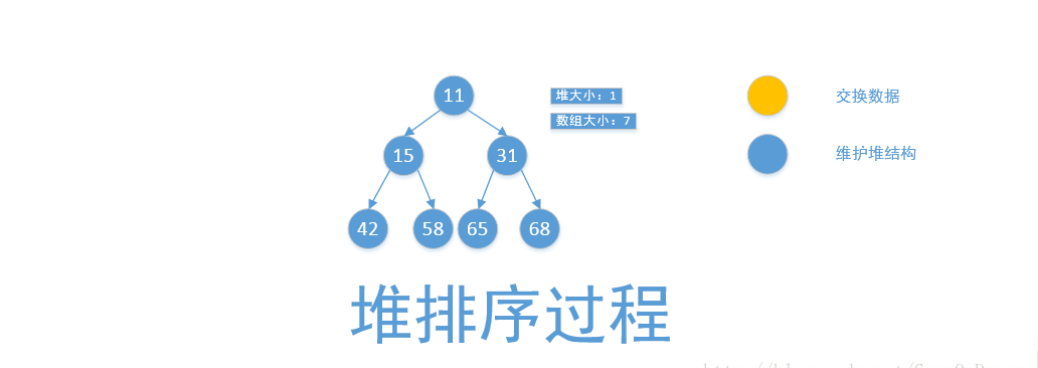
-
对于列表进行堆排序来说:在前面的学习中,我们知道,无论是addElement还是removeMin它们的复杂度都是o(logn)。但是我们要注意的是,这个复杂度是在添加或者删除一个元素的情况下的复杂度。而我们进行排序的时候,是需要添加且删除n个元素的,因此,我们分别要进行这两个操作n次,以满足对n个元素进行排序。所以最终复杂度为2nlogn,即o(nlogn)
-
对于数组进行堆排序来说:从数组中第一个非叶子的结点开始,将它与其孩子进行比较和互换(如有必要)。然后在数组中往后操作,直到根。对每个非叶子的结点,最多要求进行两次比较操作,所以复杂度为o(n)。但是要使用这种方式从堆中删除每个元素并维持堆的属性时,其复杂度仍为o(nlogn)。因此,即使这种方式的效率稍好些,约等于2*n+logn,但其复杂度仍为o(nlogn)。
-
-
教材学习中的问题和解决过程
-
问题1:书中对于优先级队列的内容其实挺简略的,所以我上网找一下优先级队列的内容
-
问题1解决方案:
队列就是先进先出的一种形式,而优先级实际上就是根据某种标准进行排序,高级的就先排,对于相同级别的就根据先进先出的队列的要求进行排序,优先级队列也叫优先权队列。
对于优先级队列的特点:
1.优先级队列是0个或多个元素的集合,每个元素都有一个优先权或值。
2.当给每个元素分配一个数字来标记其优先级时,可设较小的数字具有较高的优先级,这样更方便地在一个集合中访问优先级最高的元素,并对其进行查找和删除操作。
3.对优先级队列,执行的操作主要有:(1)查找,(2)插入,(3)删除。
4.在最小优先级队列中,查找操作用来搜索优先权最小的元素,删除操作用来删除该元素。
5.在最大优先级队列中,查找操作用来搜索优先权最大的元素,删除操作用来删除该元素。
注:我们在删除之后,要根据要求对之后的元素进行重新的排列,这个时候,我们可能出现多种的相同优先权,所以,这个时候就应该根据队列的要素,进行先进先出的进行排序,因此这也提醒我们,我们在写代码时,我们要对进入队列的顺序进行记录。
6.插入操作均只是简单地把一个新的元素加入到队列中。 -
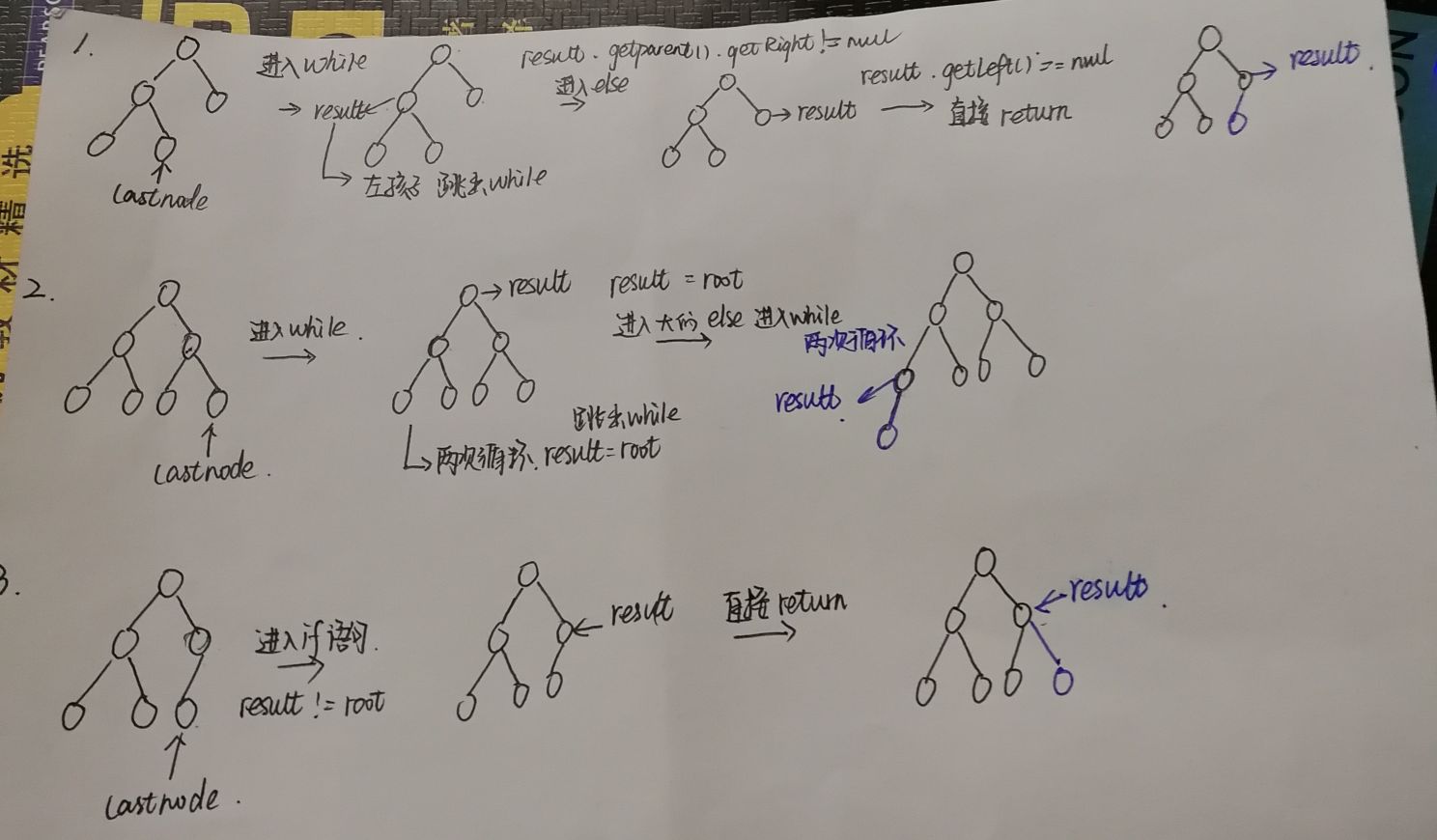
问题2:我和曾程在宿舍看书的时候,看到getNextParentAdd这段代码不理解,我俩都处于有点蒙圈的状态。
private HeapNode<T> getNextParentAdd() {
HeapNode<T> result = lastNode;
while ((result != root) && (result.getParent().getLeft() != result))
result = result.getParent();
if (result != root)
if (result.getParent().getRight() == null)
result = result.getParent();
else {
result = (HeapNode<T>) result.getParent().getRight();
while (result.getLeft() != null)
result = (HeapNode<T>) result.getLeft();
}
else
while (result.getLeft() != null)
result = (HeapNode<T>) result.getLeft();
return result;
}
- 问题2解决方案:后来晚上听馨雨和仇夏讨论的时候,我俩也去听了下,就懂得了。
下面是一个自己画的图的过程:
代码调试中的问题和解决过程
-
问题1:在进行ArrayHeap的测试时,出现这样的情况,它删除之后,后面总是多出来一个数字,不知道为什么?

-
问题1解决方案:后来我问了谭鑫,谭鑫说,书中的removeMin少写了一条语句,就是
tree[count - 1] = null;
然后我把它加上就正常了

后来他给我讲原因:
T minElement = tree[0];//最小的元素是根结点,也就是数组的0位置处
tree[0] = tree[count-1];//这个时候,将最末叶子结点放在了根结点处,准备进行重排序
tree[count-1] = null ;//将放在上面的那个最末叶子结点去掉,否则就会多出来
heapifyRemove();//进行重排序
代码托管
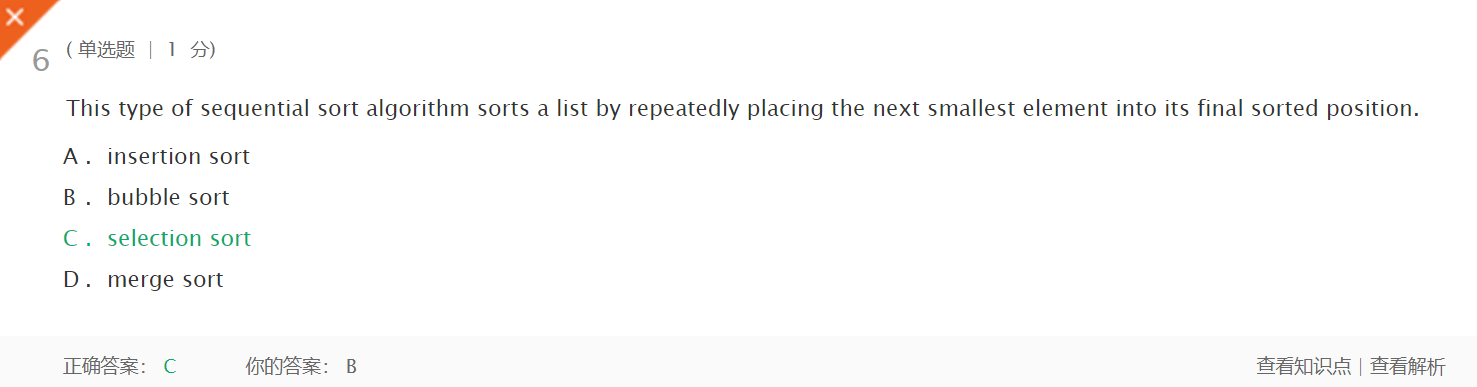
上周考试错题总结
-

-
这个是马虎的,我后来看IDEA知道了compareTo返回的是boolean型
-
-
选择排序算法通过反复地将某一特定值放在它的列表中的最终已排序位置从而完成对某一列表值的排序
-

-
插入排序算法通过反复地将某一特定值插入到该列表某个已排序的子集中来完成对列表值的排序
结对及互评
评分标准
-
博客中值得学习的或问题:
- 课本内容总结的很详细
-
代码中值得学习的或问题:
- 有的问题我没遇到过,看到他的也算是种收获
点评过的同学博客和代码
- 本周结对学习情况
- 20172325
- 结对学习内容
- 一起学习了十二章的内容
- 共同学习了堆的排序
- 讨论了堆的添加和删除
其他(感悟、思考等,可选)
第十二章老师讲的比较简略,主要讲了堆排序的内容,说是很有用的,而且我也听懂了,哈哈哈!
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 6/6 | |
| 第二周 | 985/985 | 1/1 | 18/24 | |
| 第三周 | 663/1648 | 1/1 | 16/40 | |
| 第四周 | 1742 /3390 | 2/2 | 44/84 | |
| 第五周 | 933/4323 | 1/1 | 23/107 | |
| 第六周 | 1110/5433 | 2/2 | 44/151 | |
| 第七周 | 1536/6969 | 1/1 | 56/207 | |
| 第八周 | 1403/8372 | 2/2 | 60/267 |