P1033自由落体

传送

杯具wa，惨痛的教训————别写一些情况多到要打表的判断，写着写着就wa了

这个题，我主要死在判断上了

第一遍20分的思路：看小车此时跨越几个整数点。因为我求出了此时小车的车头坐标和车尾坐标。然鹅人家是double类型的。

                 判断打表累死你~~~    ______可爱的打表（打表向我扔了一个unaccetp并表示不想理我）

难道我们只能从0到n-1判断一遍了吗？？？好吧只能这样了（我的时间复杂度233）<---一位被TLE整怕了的蒟蒻。

其实这样复杂度并不高，只有o(n)

判断解决了，就很好办了。这个题的小球很迷，它不会被车撞飞，而且它与车只差0.0001时会被接到（是在车前/后0.0001而不是在车上方0.0001（脑回路清奇的我思索了两遍才意识到这个问题））。

因为直接分析略有麻烦，所以我们分两段分析：

1.所有小球落到k（小车高度）时，小车接住的球数。设此时,小车头坐标为s11,尾坐标为s12。则接住的球数为从0到n-1判断一遍，看有几个球在[s11,s12]中。

2.小球从k落到地面时，小车接住的球数。设此时小车头坐标为s21，则又接住的球数为从0到n-1判断，看有几个球在[s21,s12]中。

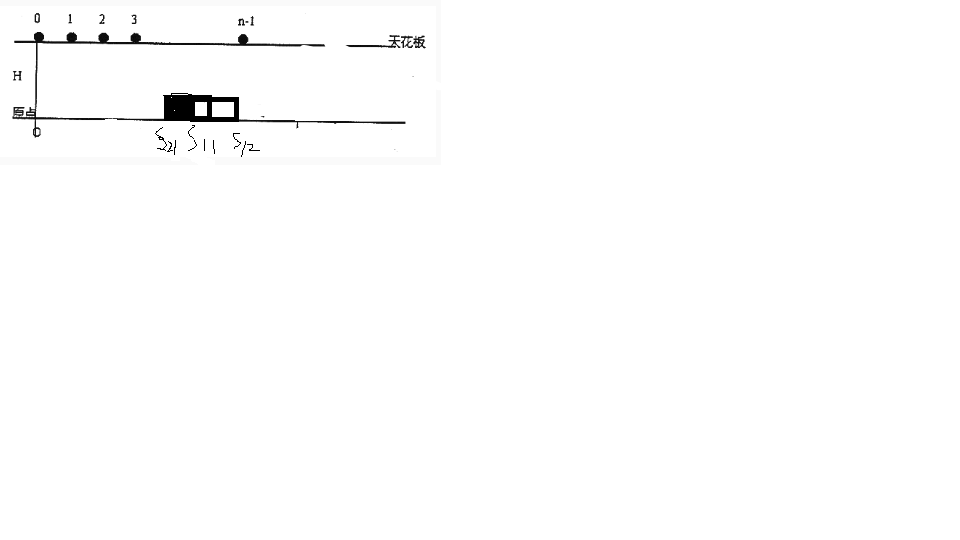
以上两次接住的球数加起来就是答案。（画工有限，忍一忍吧233）

代码奉上：

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
double g=10,s1,h,v,l,k,n,t1,s[3][3],t2;
int ans;
int main()
{
    scanf("%lf%lf%lf%lf%lf%lf",&h,&s1,&v,&l,&k,&n);
    t1=sqrt((h-k)/5.0000);//t1用来求s11,s12;
    s[1][1]=s1-v*t1;s[1][2]=s[1][1]+l;
    for(int i=0;i<n;i++)
    {if(i>=s[1][1]-0.0001&&i<=s[1][2]+0.0001)ans++;
    }//判断
    t2=sqrt(h/5.0000)-t1;
    s[2][1]=s[1][1]-v*t2;
    for(int i=0;i<n;i++)
    {if(i>=s[2][1]-0.0001&&i<=s[1][1]-0.0001)ans++;
    }
    printf("%d",ans);
}