数据结构



堆:就是priority_queue
讲完了 ------------------by dms

树上倍增qwq
作用:求最短路(在树上)
A走到lCA+B走到LCA就是最短路
lca求法:
朴素:
求出每个节点的深度
step1:如果a的深度比b的深度小,就交换a,b(为了处理方便)
step2:把a跳到b的深度(a不停的向上跳,当a,b处于同一深度的时候停止)
step3:a,b一起向上跳,直到a=b为止
复杂度:O(深度)
我们发现这时如果树是个链的话就炸了
我们想想怎么优化
我们可以在向上跳的时候优化(也就是2,3步)
我们设p[x][i]表示x的2i的祖先节点,so p[x][i]=p[p[x][i-1]][i-1]
why?就像爷爷是爸爸的爸爸一样
step2优化:a和b会有深度差delta,我们把delta转换为二进制,如果delta的第i位是1,则a就变成p[a][i](注意这里从高位到低位循环)
step3优化:我们发现a,b到了lca之后,再往上跳就都一样了,我们很难确定lca,但是可以确定lca的儿子,即最浅的a≠b的位置。
我们循环i从16(当然也可以是20神马的)到0,如果p[a][i]≠p[b][i],则让a=p[a][i],b=p[b][i],一直向上跳
我们还可以用lca求树上任意两个点的路径
我们求出根到a的路径+根到b的路径,再减去2*根到lca的路径
其实差分问题都可以用lca来做辣(比如还有乘法什么的)

用途:查询[l,r]的区间最大值,不支持修改
mx[i][j]表示[i,i+2j-1]这个区间的最大值,可以预处理
查询:求出区间长度l,那log2l就可以把整个区间分成两段(可能会有重叠,不过木有瓜系),设j=log2l,那查询的区间就是max(mx[i][j],mx[r-(1<<j)+1][j](这里i是左端点,r是右端点)
预处理:st[i][j]=max(st[i][j-1],st[i+1<<(j-1)][j-1]

神马是哈希?就是一个函数。平常说的哈希就是将一个字符串转成一个数。
怎么整???
我们先考虑一个字符串是几进制的数(是几进制看心情咯,不过建议取一个大于字符集大小的质数)
然后暴力计算,如果字符串里面有数字肿么办?
取ASCLL码值呗。然后我们发现转着转着就爆了,所以我们要取模。可以模大质数,也可以自然溢出(unsigned longlong)
HASH有冲突怎么办?认命双重哈希,就是设计两个模数。如果还用冲突,那就3个
我们现在能够求出一个整串的哈希,但是我们想要求子串,怎么办?
我们可以求每个前缀的哈希值
举个栗子:dingmingshuohaokeai
d:d
di:d2+i
din:d3+i2+n
ding:d4+i3+n2+g
有什么用呢?
假设我们要求ing的哈希,那f(ing)=f(ding)-f(d)*p3
那化成一般的式子就是f(子串)=f(前缀)-f(不是子串的部分)*p子串长度
即hash(i,j)=hash(j)-hash(i-1)*pj-i+1
要求:快,准,尽可能避免冲突(只有神仙能做到qwq)

上面是路径压缩qwq
用fa[x]表示x的父亲.
合并a,b:让a的祖宗认b的祖宗为爹。
找x的祖宗:如果x的祖宗是自己,就返回x,否则返回fa[x],这里常用路径压缩进行优化,即返回时顺带把x的父亲,爷爷等等的fa都改成x的最高的祖宗


我们接下来要种几棵仙线段树
线段树是用来干什么的呢?当然是等它开花结果卖钱了(雾)
线段树支持区间(单点)修改,区间(单点)查询
我们种下线段树之后第一步是什么?给树浇水(雾)
我们先来考虑又直接又暴力的单点修改
就直接修改呗,都说了很暴力辣
那区间查询呢?
我们递归找答案。如果当前节点表示的区间被要求的区间完全覆盖,就不用往下再递归了,直接返回。否则看要求的区间与当前节点的哪个儿子有交集。哪个有交集就递归哪个。
我们再来考虑区间修改。
我们发现暴力区间修改的复杂度是O(nlogn)的,比不用线段树还慢qwq
所以我们需要懒标记来加速
这样就很像我们的区间查询了。也是递归在区间上打懒标记,递归的规则与区间查询一样。
有了懒标记就要注意了,如果我们不是对节点代表的这整个区间进行操作,那就要标记下传(不管是查询还是修改)。

qwqqwq
n个节点,n-1条边,说明这个图是棵树
对三个人两两求lca,会有以下三种情况(其中ABC分别代表那三个人)
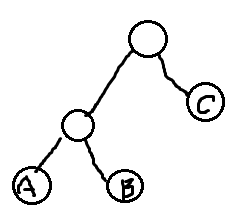

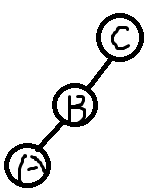
我们发现一定会有两组lca是重复的,那剩下那个不同的lca就是集合地点辣
(打表找规律得,没有证明)

qwqqwq
维护两个堆,一个大根堆,一个小根堆。一直往大根堆里面塞,保证大根堆里面的元素少于k/2+1个。如果出现元素个数≥k/2+1,就弹掉堆顶,把堆顶塞进小根堆。这样的大根堆堆顶就是答案。
 我们发现,越先被合并的那堆被算进答案的次数就越多,所以我们要合并尽可能小的两堆
我们发现,越先被合并的那堆被算进答案的次数就越多,所以我们要合并尽可能小的两堆
贪心完毕,没有代码
据说这是哈夫曼树的模型

太难了不会qwq


这里可以由低海拔的点走到高海拔的点,其中T是输入给定的
我们按照相邻两个格子的高度差建边。
那这玩意不就是第T-1短的边权吗
推导:由于T已知,而且n-1条边可以连通n个点,那么当连了T-1条边的时候,就能够到达T个点了。为了让D最小,所以我们先把所有的边按照边权(也就是高度差的绝对值)从小到大排序,然后一条一条的连边。这时D=第T-1短的边权

(树状数组模型1)
我们先想暴力怎么求逆序对数
我们可以双重循环扫描比i大且在i前面出现的的所有j,然后加一加
我们在暴力的基础上再进行一番优化
我们发现,每次枚举i都暴扫一遍真的很浪费有木有,那怎么统计i与1~i-1到底构成了多少个逆序对呢?
我们把ai的权值作为树状数组的下标,每出现一次权值为i的数,那就对树状数组进行一次操作(从c[i]开始),然后sum(a[i])就是比a[i]小的数出现的次数,那比a[i]大的数出现的次数就是i-sum(a[i])
然后我们发现空间炸了,因为a[i]实在是太大了
那我们可以离散化对吧
然后就能A了

在这里因为y是递增的,所以我们可以无视掉y的存在,然后只要求x<当前的x的所有星星就行了
我们注意到m肥肠之小
所以开m个树状数组进行操作
每个树状数组的c[i]记录下标为i的序列中的数%m后是否等于当前这个树状数组的编号
如果要改变,就直接改,如果要查询,就在第mod个树状数组里面查询,sum(r)-sum(l-1)就是答案

一:平衡树(set,splay)因为保证有序,所以只需要比较前驱和后继哪个更靠近当前查询的数就好了
二:线段树qwq
以权值为下标,建立线段树
维护区间最小值,区间最大值
以当前查询的数为界,看左边区间的最小值,右边区间的最大值比较哪个更靠近当前查询的数

线段树板子2qwq

我们想到求斐波那契数列可以用矩阵乘法,对于ai+x,就相当于原来的数*矩阵的x次方
式子如下:
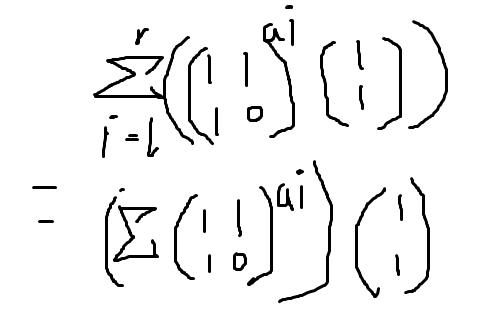
然后线段树维护矩阵加的和就好了

qwq
在昨天分块的时候说到longlong 以内的数最多被开6次根号,就会成熟。这个题也是利用这个性质。如果这个区间他没有成熟,就暴力开根,如果成熟了,就不要管他。求和就线段树求和。

从5入手emm
要关注小的数或者是取模数,这一般是入手点
我们开一个s数组,s[i]记录mod 5=i的下标对应的数的和
线段树的节点记录对应区间上的s数组
序列:0 1 2 6 7 8 9 11

合并:我们发现合并区间[1,2]的时候,只需要把10000向右转一位即可
即看当前节点对于其父节点来说是左子树还是右子树,如果是右子树就转1位,左子树不转

mex:当前区间内的没有出现过的最小的非负整数。 这道题我们要离线做(在线做是真的不好做)
我们按照询问的l排序。接下来我们可以求出1~i的mex(也就是前缀) 我们再考虑1~i的mex和2~i的mex有什么关系。如果a[1]要小于1~i的mex,那么2~i的mex就是a[1] 推广到一般的r-l的mex与r-l+1的mex,就是让后面大于a[l]的mex变为a[l]就好了辣

len至少是3,那我们只要找到一个len等于3的等差序列,就有解了
我们开一个bool数组p,p[当前出现过的数]=1
不断枚举作为等差数列中间项的数,检查这个数两边的01是否对称,如果不对称,则证明没有出现的那个数在后面一定会出现(因为是1到N的排列),此时一定有解。如果一直对称,则无解