

数据范围:O(n3)
弗洛伊德跑出两两之间的最短路
然后加一加判一判

跑单源最长路
复杂度:O(n2logn)
因为边数是n2的

先跑一遍1为源点的最短路
再建一张把所有有向边都反过来的最短路(1还是源点)来跑

一:
在跑dij的时候在维护的数里面再塞一个当前的费用,当费用>k的时候就不更新(下一个)
二:
建n*k个点的图

然后跑个dij

①:二分答案,把大于等于二分的答案的边加进图中,判是否连通
②:跑dij,更新条件换成if(d[v]>min(d[u],w)) d[v]=min(d[u],w)
③:kruskal找最大生成树,当点1和点n第一次连通的时候,加的那条边就是答案


这里酋长的等级不一定是最高的
边权是优惠后的价格
由贵的物品向便宜的物品建边(边权是优惠的价格),从1点开始跑最短路,dis[i]+i的原价是最小价格
考虑等级限制:
枚举等级的区间[l,l+m],其中一定包含酋长的等级
然后枚举的每一个区间跑一次dij
注意人的等级是分散的(类似[1,10]和[2,11]里面包含的人是一样的),所以可以以人的等级为左端点
这样就是n次dij,n<=100
复杂度还是承受的了的

显然dij被卡爆了
于是我们可以想到一些奇技淫巧
线段树实现dij怎么样?
恐惧.jpg
我们想想怎么优化dij
我们发现priority_queue里面会有很多冗余节点,我们可以合并
但是priority_queue不支持合并
所以我们需要一些奇怪的堆(什么斐波那契堆什么配对堆)
but好像得手写?!!
不会....
平板电视,你值得拥有
既然不会正解,那我们可以骗分阿
继续用stl的priority_queue
因为输入的边有一部分是随机数据生成器生成的边,所以对最短路的影响似乎不大
而且输入的边似乎只有1e5左右的样子
所以我们就把随机数据生成器生成的边扔掉,说不定就AC了
诶嘿AC了?![]()
好了这题做完了
插句题外话
priority_que怎么搞合并?
合并两个堆a,b:把点少的那个堆拆掉,把点一个一个放到另一个堆里面,复杂度O(nlog2n)
合并许多堆:二分式拆法
Prim:

我们可以把dij搞一搞然后变身prim
证明:

kruskal
按边权从小到大排序,如果选当前边会成环,则不选,否则就选,直到考虑完所有的边
其实复杂度卡在排序上了(mlogm)
证明需要拟阵的知识

独立集就是满足遗传性和交换性的集合
| |这个是集合的元素个数
线性相关:
什么是向量:类似一行数组成的东西

上面就是个向量,格子里面可以填数
如果我们有向量a,b,c
x1*a+x2*b+x3*c=0
则向量a,b,c线性相关
生成森林:
就是一些不成环的边辣
遗传性证明:如果有一个图没有环,那么去掉任意的边之后都不会形成环,证毕
交换性证明:
我们设A的边数比B的边数少(A,B都是无向生成森林)
既然B不是个环,那么从B里面拆下来一条边安到A上,那么A完全可以安成B原来的样子,所以交换性成立
(xjb玄学证明qwq)

所以拟阵最优化问题就是kruskal
kruskal的正确性好像就是这样的叭
有什么用呢?如果遇到拟阵贪心题就可以用kruskal就好了

最小生成树....(撑死就是边多了一点)

最小生成树+1
最小生成树+2???

先建一个超级水库,连边就是在i建水库的代价
然后最小生成树(保证每个点都能与建出来的超级水库连通)

这大概是个树
会有一些毒瘤的无法到达的点,我们就把连着这些点的边去掉
然后选出一棵树(不能带环)
然后最小代价就是最小生成树
kruskal怎么排序?
按照边的较低的点从大到小排序,按长度从小到大排序
为什么第一关键字是从大到小排序?
如果是从小到大排序,则只能保证比当前点高度小的点是连通的,但是可能会有毒瘤情况导致求出来的解不够优
emm还是举个例子叭
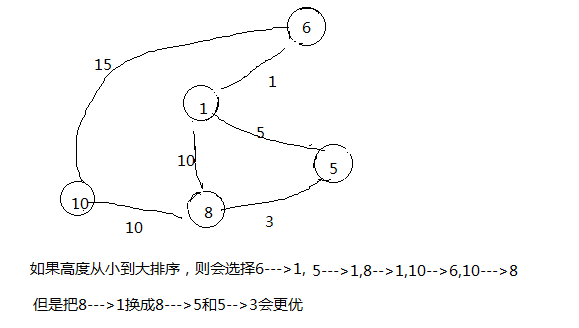
另一个神奇的思路:
分层建图,将高度相同的点建在同一层,同一层内是无向边,不同层之间是有向边,同一层内搞最小生成树,然后通过有向边传递到下一层,最后取边权最小值

咕咕咕~?
晚上网络流time走起





k进行二进制拆分


还有tarjan+并查集(离线,O(n))
dfs序+RMQ搞lca:
我们先进行dfs,每到达一个点,就把一个点放进一个序列里面(如果回溯时到达序列中有的点,则再放一遍)
如果要算a,b的lca,就找到最后出现的a和第一次出现的b,它们中间一定会有它们的lca
这样它们中间的那个深度最浅的点就是lca了(用RMQ维护深度最浅的点)


树链剖分

一种叫重量剖分,另一种叫常量剖分
默认重量剖分

注意重链的出发点不一定是根,可以是任意的节点
每一个点必定属于一个重链
如果从任意一点网上走,则经过的重链的条数和轻边的边数是等级别的(都是logn级别的)
why?
轻边和重链是交替走的,因为如果走完一条重链,再走一条重链,那它们就是一条重链了(即不存在两条连续的重链)
所以重链的条数≤轻边数量+1
如果我当前走过了一条轻边,则说明我走过的那个点的父亲的子树至少是那个点的子树的两倍。所以如果我一直走轻边,只需要最多logn次就能走完这棵树。
dfs:
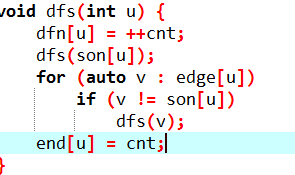
树链剖分求lca

先判ta是否==tb
如果a,b有祖宗关系:看谁的深度浅,谁就是lca
深度较深的:到a-->topa,topa-->轻边,然后递归求解
复杂度:o(logn)

树链剖分的特点:重链在树上是连续一段
求a到b路径上的信息:先找到lca,然后就是一段重链,一个轻边blabla
把树摊成个区间,这样就可以求一段区间的最值
求最值:线段树来维护(只维护重链,轻边暴力解决)

就是要求两个操作:
1.把某个边权的值改为t
2.求a到b路径上的最小值
先把边权摊到儿子上
改边权:找到儿子u,再找到dfn[u],在线段树里单点修改
求最小值:找到lca的那两条链,把链上的重链所在序列的区间在线段树里找到最大值
bzoj 1036

...和上题差不多
操作3:把求最大值换成求和
线线线线线段树

这个线段树有点难qwq
看左儿子和右儿子中间那个相不相同
染色的tag

先求个最小生成树,不在的边就不管
如果在呢?
树会被分成两块,只需要在非树边里面找一条权值最小的连接这两个块的边就可以了
一个非树边能够缝合一个数:当去掉它包含的一段链里的边
所以可以在树上每个边搞一个权值(初始为inf),然后与覆盖它的非树边的权值取min,即可快速查询可以缝合树的最小边权


qwq
证明:没有

缩点+拓扑排序
如果不考虑n的大小:弗洛伊德传递闭包
更好一点:传递闭包
大小为k的强连通分量贡献:k2
然后求一个scc可以到达的scc: bitset压位
然后再考虑每个scc的大小(原数*k2)
bitset:
bitset<1000000>a
a就是一个长度为1000000的二进制数
a[i]访问a的第i为
下标从0开始

缩点,统计出度为0的点
1个点:出度为0的点的那一坨牛
>1:没有牛

缩点
T1:统计入度为0的点的数量
T2:max(入度为0的点的数量,出度为0的点的数量)
T3:给出连边方案(雾)
总之要把入度为0的点和出度为0的点弄没
找一个出度为0的点,让它连向一个无法到达的入度为0的点,重复这个操作