luoguP1502过河题解

日常吐(fei)嘈(hua)

这道题作为最近卡了我3天的dp题(最后还是在题解的帮助下冥思苦想才过掉的题)，窝觉得此题肥肠之脑洞，写此博客纪念

题解

过河


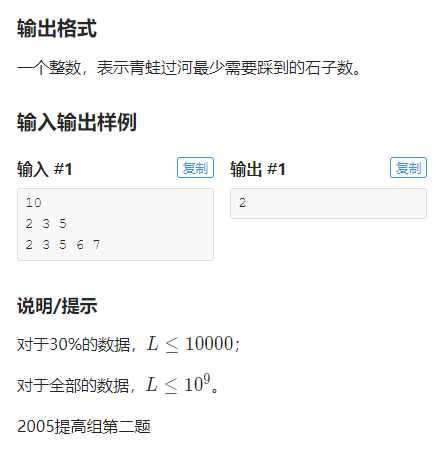
先来日常手玩样例：

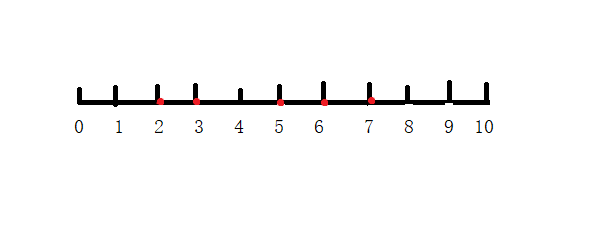
咦感觉怎么手玩答案都像是3的亚子？？？
吓得我打开了讨论组
我们发现题目没说一定要踩到石子上，所以类似0->2->4->7->10的走法也是可以的
手玩样例成功√
容易看出来这是个dp,因为走法无后效性。
那么我们思考dp式子。设(dp[i])表示跳到距离原点(i)的地方，最少踩过的石子数。因为最终可以跳出(L),所以答案是(min{dp[i],i in [L,L+t]})。转移就是(dp[i]=min{dp[i-j] }+是否有石子,j in [s,t])
然后我们康康数据范围

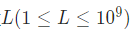
噫，好，我炸了
显然空间是开不下的。就算用各种奇技淫巧把空间优化到开的下然后发现(O(1e9))的(dp)它(T)了。
于是我们考虑用各种奇技淫巧来减小(L)
我们发现石子数量(M)相比于(1e9)来说小的可怜，只有100。这样一定会出现两个石子中间距离特别特别大的现象。而且(s,t)最大是10，显然对这些中间没有石子的区域进行dp是个很大的浪费。那么我们想办法把这些距离压缩掉。

我们来观察一下中间没有石子的区域的dp值是如何转移的。

其中([s_i,t_i])是跳i步能达到的点。我们发现(s_i=0+i imes s,t_i+i imes t).而且发现当某个(s_i=t_k)时，就会产生有两个([s_i,t_i])接起来辣！然后(dp)值也就会出现和前面相同，此时就可以压缩掉了,发现当上面的(i=t,k=s)时一定会出现这种局面,所以两个石子间的距离遇弱大于(s imes t),就可以把距离压缩成(s imes t)。
当然，对于(s==t)的情况是要特判的
因为(s==t),所以只能跳s的倍数，直接看s的倍数的地方有多少石子就可以了
代码：

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<vector>
#include<queue>
#include<map>
#include<ctime>
#include<cstdlib>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef __int128 i128;
const int inf=2147483647;
inline int read()
{
	char ch=getchar();
	int x=0; 
	bool f=0;
	while(ch<'0'||ch>'9')
	{
		if(ch=='-') f=1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')
	{
		x=(x<<3)+(x<<1)+(ch^48);
		ch=getchar();
	}
	return f?-x:x;
}
int l,s,t,m,sz[109];
int dp[10000009];
int ys[10000009]; 
int main()
{
	l=read();s=read();t=read();m=read();
	for(int i=1;i<=m;i++)
       sz[i]=read();   
    if(s==t)
    {
    	int ans=0;
    	for(int i=1;i<=m;i++)
    	 if(sz[i]%s==0) ans++;
    	printf("%d",ans);
		return 0; 
	}
    sort(sz+1,sz+1+m);//输入不一定按升序
	int qwq=s*t;
	int lst=0;
	for(int i=1;i<=m;i++)//压缩距离
	{
		int qaq=sz[i]-lst;
		lst=sz[i];
		if(qaq>=qwq) qaq=qwq;
			sz[i]=qaq+sz[i-1];
		ys[sz[i]]=1;
	}
	int en=sz[m]+qwq;//考虑可以跳出l,所以最后距离要大一些
	memset(dp,0x3f,sizeof(dp));
	dp[0]=0;
	for(int i=1;i<=en;i++)
	{
		for(int j=s;j<=t;j++)
		 if(i-j>=0) dp[i]=min(dp[i],dp[i-j]+ys[i]);//上面的dp式子
	}
	int ans=inf;
	for(int i=sz[m];i<=en;i++)
     ans=min(ans,dp[i]);
    printf("%d",ans); 
}