先了解一下两个东西
最大流:从起点到终点能实现的最大的流量
通俗点解释,就好比你有很多货物要从源点点运到汇点点,有向图中的一条边代表一条公路,每条公路有固定的货物装载限制(容量),对每条公路你只能运输一定数量的货物,问你每一次运输最多运到汇点点多少货物。
最小割:对于一张流量图G,断开一些边后,源点s和汇点t就不在连通,我们将这样的k条边的权值(即最大容量)和求和,求和后的值称为割。显然,对于一张流量图G,割有很多个且不尽相同。我们要求的就是所有割中权值最小的那一个(可能不唯一),即花最小的代价使s和t不在同一集合中。
引理: 最大流最小割定理
- 任意一个流都小于等于任意一个割
- 构造出一个流等于一个割
- 在一张流量图G中,最大流=最小割。
任意两边的交点在顶点上的图我们称为平面图
这道题很容易看出来是求最大流,那么可以转化为最小割来做
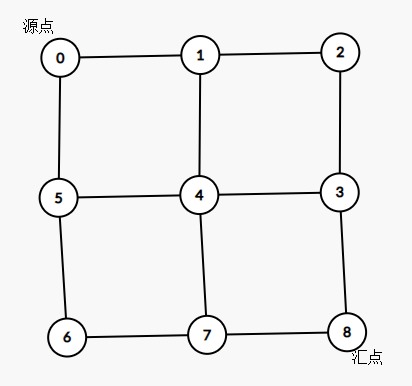
比如对于这样一张图,我们发现如果要使源点和汇点断开,相当于去掉一些边
假如我们去掉连接4,5的边

如图,相当于是在上下两个图形上面连了一条边,而这条边的边权就是4,5这条边的边权
那么这个问题不就变成了这样

(忽略掉原来的九个点)
在这张新图上面找最短路
我们发现有很多连到图形外面的点,我们不妨把他们合并一下
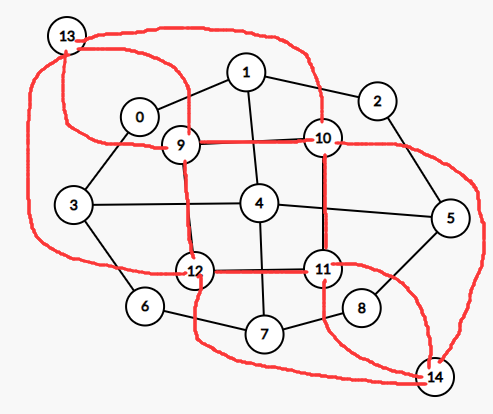
(标红的是对偶图的边)
那么就是寻找源点13->汇点14的最短路
定理:平面图的最小割=对偶图的最短路
对于样例的数据就是这样
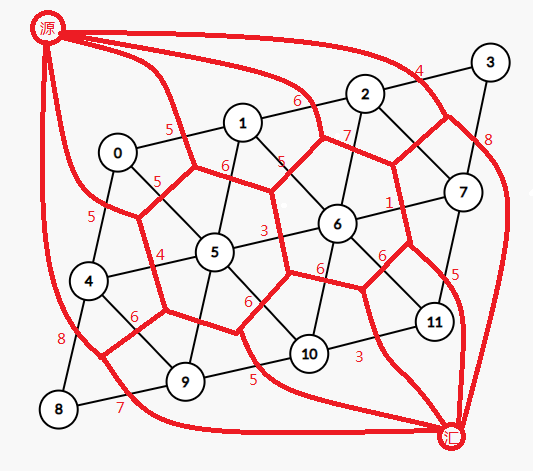
只需要从源点到汇点跑一遍最短路就行了