任何进制转成十进制,使用按权展开法,注意小数点。
十进制转成任意进制,使用短除法。
1个字节有8个位,每位分别用二进制的0和1来表示。分为无符号数和有符号数,下面以有符号数来说明,有符号数最高位是符号号,0表示正,1表示负。
原码:1 表示 0000 0001 -1表示 1000 0001 相加得 1000 0010 ,相当于-2,所以原码不直接用作计算。
反码:如果是正数,则与原码相同;如果是负数,除符号位之外,所有位在原码基础上反转, 如 1表示 0000 0001 , -1表示 1111 1110, 相加得 1111 1111,该值为负数,取其原码,则是 1000 0000,得出 -0,结果正确,但仍然有点古怪。
补码:如果是正数,则与原码、反码相同,如果是负数,则在反码基础上+1,比如 1表示为 0000 0001, -1 表示 1111 1111,相加得 1 0000 0000 ,即是 0,这个看上去最符合我们想要的结果。
移码:一般用于浮点运算中的接码,不管是正数还是负数,移码都是在补码基础上将首位取反。比如1表示为 1000 0001, -1表示 0111 1111,相加得 1000 0000,即 -0。
表示范围:
原码和反码的范围相同,补码比原码和反码的取值范围大1,这是因为补码的0只有0000 0000 这一种形式,而原码和反码的0有 0000 0000 和 1000 0000 两种形式。
原码和反码: -(2^(n-1) - 1) ~ 2^(n-1) -1
补码: -2^(n-1) ~ 2^(n-1) -1
其中 n 表示位数,比如8位,原码和反码的范围是 -127~127,补码范围是 -128~127
浮点数:
浮点数表示 N = M * R^e
其中,M称是尾数,e 是指数, R是基数。尾数使用一位非0数表示。
浮点数运算时,有三个步骤:对阶、尾数计算、结果格式化。
比如 0.123 * 10^2 + 0.1 * 10^3 会先转成 0.0123 * 10^3 + 0.1 * 10^3 转成 (0.0123+0.1) * 10^3 = 0.1123 * 10^3 = 1.123 * 10^2
主机:这里的主机实际只包含CPU和内存
CPU包括运算器和控制器
其中运算器包括4个部分:
1、算术逻辑单元ALU
2、累加寄存器AC
3、数据缓冲寄存器DR
4、状态条件寄存器 PSW
控制器包括4个部分:
1、程序计数器 PC
2、指令寄存器IR
3、指令译码器
4、时序部件
Flynn分类法——计算机体系结构分类
1、单指令单数据流 SISD
控制部分只有1个,处理器只有1个,主存模块只有1个,代表是单处理器系统、单片机。
2、单指令多数据流 SIMD
控制部分只有1个,处理器有多个,主存模块有多个,各处理器以异步的形式执行同一条指令,代表是并行处理机,阵列处理机。
3、多指令单数据流 MISD
理论模型,实际不存在。控制部分多个,处理器1个,主存模块多个。
4、多指令多数据流 MIMD
控制部分、处理器、主存模块都有多个,能够实现作业、任务、指令 等全面并行,代表是多处理机系统、多计算机,我们使用的计算机应该都属于此类吧。
两种指令系统:CISC 和 RISC
CISC:复杂指令系统
指令数量多,使用频率差别大,可变长格式,支持多种寻址方式,使用微程序控制技术实现,研制周期长。超级计算机就属于此类。
RISC:精简指令系统
指令数量少,使用频率接近,定长格式,大部分为单周期指令,操作寄存器,只有 Load/Store操作内存,支持较少的寻址方式,增加 了通用寄存器,硬布线逻辑控制为主,适合采用流水线,优化编译,有效支持高级语言。我们使用的计算机就属于此类。
流水线:多条指令并发执行的一种实现技术。
对于一条指令的执行,分为三个步骤,分别是:取指、分析和执行。其中最耗时的一个步骤时长,称为流水线的周期。
流水线的总时长计算分为两种,流水线分为流水线建立阶段和流水线运转阶段,建立阶段需要耗费一条指令的时长:
1、理论公式
(1条指令的所有步骤总时长) + (指令条数-1)*流水线周期
2、实践公式
如果一条指令中每个步骤耗时不同,则会产生时间片不工整,需要等待,所以可以让每一个步骤耗时都设置成流水线周期。这样的话,公式就是:(1条指令的步骤数*流水线周期) + (指令条数-1)*流水线周期
考试中的选择题优先使用理论公式,如果理论公式没有结果,则使用实践公式。
流水线吞吐率:单位时间内流水线所完成的任务数量。
TP = 指令条数/流水线执行时间
一条流水线的极限吞吐率是: TP = 1/流水线周期
所以如果要提升流水线吞吐率,就要想办法降低流水线周期。
流水线的加速比:完成同一批任务,不使用流水线耗时/使用流水线耗时,所以流水线加速比是越大越好。
流水线的效率:批流水线的设备利用率,在时空图上,定义为 n 个任务占用的时间区与 k 个流水段总的时空区之比。可见如果一条指令的每个步骤耗时越接近,则流水线的效率越高。
存储结构:CPU寄存器、Cache(按内容存取 )、内存(主存)、外存(辅存),依次速度递减,容量递增。
使用 "Cache+主存储器" 方案的系统平均周期 t = 命中率 * Cache周期时间 + (1-命中率)*主存储器周期时间
原理就是,当取数据时,先去Cache中找,如果找到则为命中,如果找不到,则去主存储器中找。上述公式也是依据这个原理而来。所以提高命中率,则可充分发挥Cache的作用。
Cache局部性原理:
1、时间局部性:
比如循环执行的部分
2、空间局部性:
比如数组初始化赋值
3、工作集理论:
是进程运行 被频繁访问的页面集合
主存分类
1、随机存取存储器:RAM
掉电之后数据会丢失,如内存。分为 DRAMSRAM
2、只读存储器:ROM
掉电之后,数据不会丢失,如BIOS ROM。分为 MROM/PROM/EPROM/闪速存储器
主存编址:
将内存芯片组合成存储器 ,称之为编址。
内存芯片一般用 n*m位存储器表示,表示拥有n个地址的m位存储器。
例题:内存地址从 AC000H 到 C7FFFH,共有多少K个地址单元?如果该内存地址按字(16bit)编址,由28片存储器芯片构成。 已知构成此内存的芯片每片有16K个存储单元,则该芯片每个存储单元存储多少位?
答案:112 4
解:
1、 C7FFFH - AC000H + 1/1024 = 112
2、112K * 16bit = 28 * 16K * x; 解出 x = 4
磁盘:
存取时间 = 寻道时间 + 等待时间(平均定位时间 + 转动延迟)
寻道时间: 指磁头移动到磁道所需要的时间
等待时间:等待读写的扇区旋转到磁头下方所用的时间
例题:
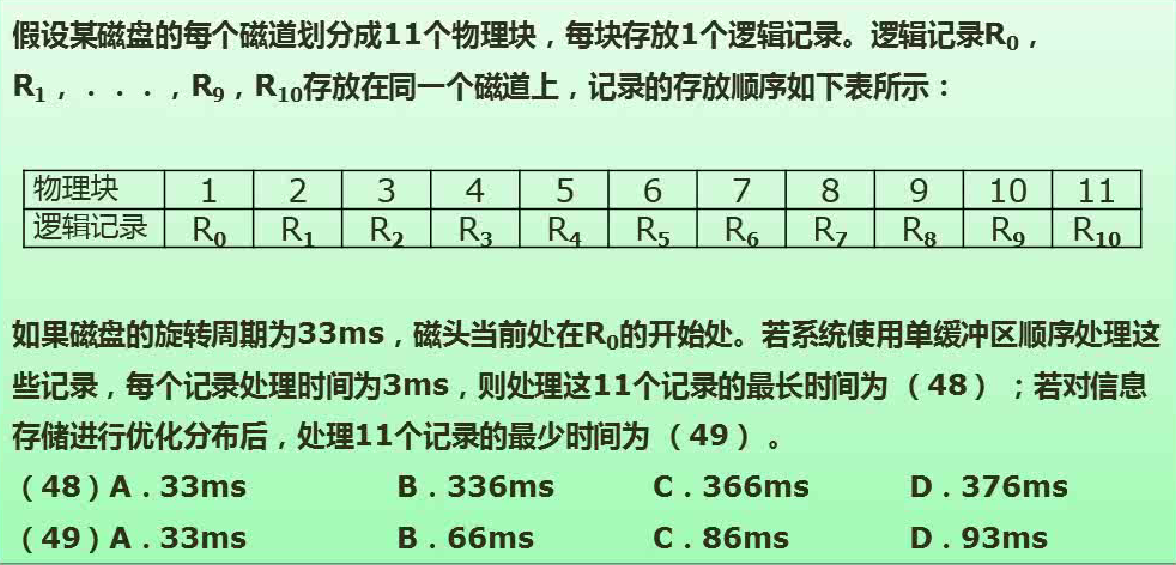
答案:366ms 66ms
总线:根据总线所处的位置不同,分为三类:
1、内部总线
2、系统总线:包括数据总线、地址总线、控制总线
3、外部总线
系统可靠性分析——串联系统与并联系统
串联系统的可靠性 = 各个子节点的可靠率相乘
并联系统的可靠性 = 1 - 并联分支的不可靠性相乘 (并联系统只有当并联分支全部故障才会故障)
差错控制:CRC 和 海明校验码
任何编码都由一组码字(code word)组成,两个码字间变化的二进制位数称为码距(code distance)。而在一种编码中任意两个码字之间最少变化的二进制位数称为该数据编码的最小码距(minimum code distance)。
比如传输A和B,用1表示A,用0表示B,则码距是1,此时无法检错,因为1和0都是合法的; 如果用 11表示A,用00表示B,则码距是2,此时可以检错,比如 10 和 01就是错的,但无法纠错;如果用111表示A,用000表示B,则不仅能检错,还能纠错,如110就是错的,应该纠正为111(默认按出错概率小的方向纠错)
检错、纠错和最小码距的关系:(了解即可)
1、在一个码组内为了检测 e 个误码,要求最小码距d 应该满足 d >= e+1
2、在一个码组内为了纠正 t 个误码,要求最小码距应该满足 d > 2t+1
循环校验码CRC
模2除法与算术除法类似,但每一位除的结果不影响其它位,即不向上一位借位,所以实际上就是异或。在循环冗余校验码(CRC)的计算中有应用到模2除法。
多位模2除法采用模2减法,不带借位的二进制减法,因此考虑余数够减除数与否是没有意义 的。实际上,在CRC运算中,总能保证除数的首位为1,则模2除法运算的商是由余数首位与除数首位的模2除法运算结果确定。因为除数首位总是1,按照模2 除法运算法则,那么余数首位是1就商1,是0就商0。
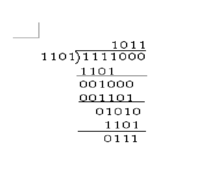
海明校验码