AGC040F
咕咕咕了好久终于编出来了
首先看成在坐标系上面走。
假设当前在 ((x,y)),强制 (xge y),要走到 ((A,B)),每一次可以进行下面几种操作。
- 走到 ((x+1,y))
- 如果 (x>y+1),那么可以走到 ((x,y+1))
- 走到 ((x,x))
不难发现 (1) 操作一定会进行 (A) 次,只需要在操作序列上面插入 (2,3) 操作即可。
那就枚举 (2) 操作的次数 (i) 进行计数。
发现 (3) 操作可以看成当前的点不动,平移当前终点在的直线和终点,形成一个新的限制。
由于我语文不是很好,所以画了一个图,大家可以简单看看。
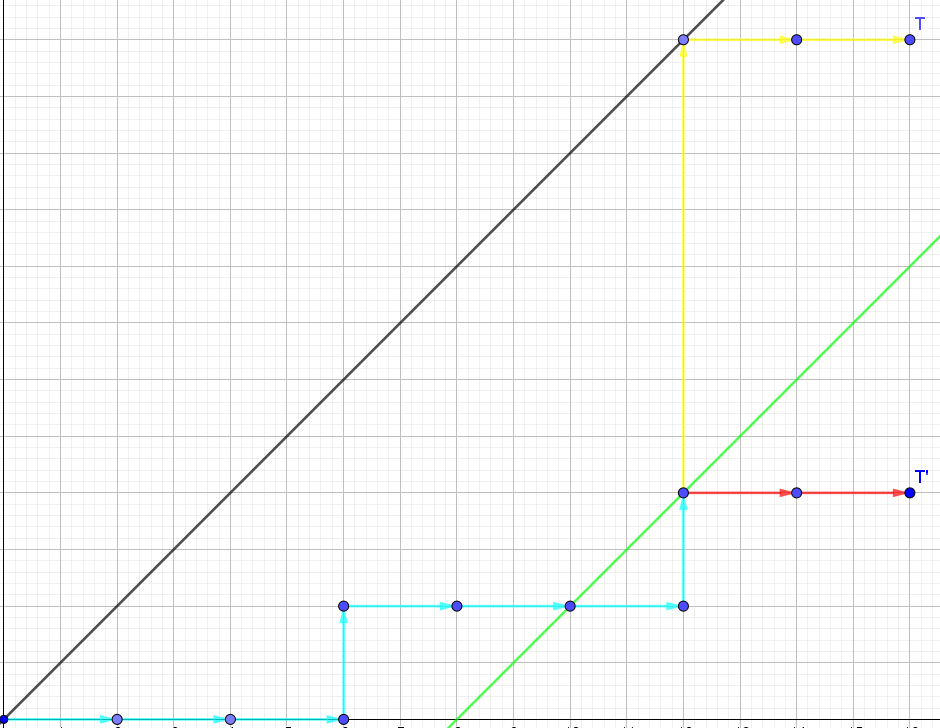
大概说的就是把黑线和 (T) 移动至绿线和 (T'),并把原路线跟着做一个变换。
观察移动直线的性质:
- 移动后 (T'=(A',B')) 满足 (A'=A,(A'-B')-(x-y)=A-B),解出来就是 ((A,B-(x-y)))
- 在之后的行动中进行操作 (2) 时,必须满足不走到平移后的线。
- 每次直线的截距减小。
假设没有进行 (3) 操作,那可以直接算方案数。
假设进行了至少一次 (3) 操作,那对于每一条路径,最后一定移到 ((A,i)),且如果时间倒流,可以依次移到 ((A,i),(A,i+1)...(A,B)),于是可以插板法算插入方案数,这题就做完了。
Code:
inline int Cal(int n, int m) { return dec(C(n + m, n), C(n + m, n + 1)); }
int main() {
cin >> n >> B >> A, init_fac(n << 1);
if (!A) return cout << 1, 0;
int res = 0;
for (ri j, i = 0, k; i <= B && i <= n - A; ++i) {
int t = Cal(A - 1, i);
if (i + A == n) Add(res, i == B ? t : 0);
else {
j = n - A - i - 1, k = B - i + 1;
Add(res, mul(t, C(j + k - 1, k - 1)));
}
}
cout << res;
return 0;
}
完全背包问题
有容量为 (m) 的背包和 (n) 种物品,每种物品的体积为 (v_i),价值为 (b_i),求体积限制内最大价值。
(nle10^6,mle10^9,a_i,b_ile100)。
考虑转化成两个较小的子问题,假设是 (x) 和 (m-x) 以内的完全背包问题,那么显然会有 (xle m-x,(m-x)-xle max{v_i})。
于是只需求体积限制 (limVin [frac{m-x}2,frac{m+mx}2]) 内的完全背包问题。
这个继续按照边界拆成两个较小的,每拆一次区间的端点值都减了一半左右,且显然区间长度最后是不会超过 (2*max{v_i}) 的。
这样拆下去,最后只需要做一个小范围(大概是 (max{v_i}*3) 这个范围内)的完全背包,然后倒着往上推就行了。
然后由于 (a_i,b_i) 范围都是 (100),所以 (n) 是个假的,离散化一下即可。
Code:
const int N = 305;
ll ori[N], f[55][N];
int n, m, V = 0, L[55], R[55], sig = 0, tot = 0;
pii a[N * N];
int main() {
m = read(), n = read();
for (ri i = 1; i <= n; ++i) {
++sig;
a[sig].fi = read(), a[sig].se = read();
ckmax(V, a[sig].fi);
}
sort(a + 1, a + sig + 1), sig = unique(a + 1, a + sig + 1) - a - 1;
int S1 = m, S2 = m;
while (S1 > 0) L[++tot] = S1, R[tot] = S2, S1 = (S1 - V) / 2, S2 = (S2 + V) / 2;
for (ri i = 1; i <= sig; ++i) for (ri j = a[i].fi; j <= V * 3; ++j) ckmax(ori[j], ori[j - a[i].fi] + a[i].se);
for (ri i = tot; i; --i) {
for (ll v = L[i]; v <= R[i]; ++v) {
if (v <= V * 3) f[i][v - L[i]] = ori[v];
else for (ll j = (v - V) / 2; j <= v / 2; ++j)
ckmax(f[i][v - L[i]], f[i + 1][j - L[i + 1]] + f[i + 1][v - j - L[i + 1]]);
}
}
cout << "max=" << f[1][0];
return 0;
}