二叉树总结—建树和4种遍历方式（递归&&非递归）

版权声明：本文为博主原创文章，未经博主同意不得转载。 https://blog.csdn.net/u013497151/article/details/27967155

今天总结一下二叉树。要考离散了，求不挂！二叉树最重要的就是 建立、4种遍历方式。简单应用。怎样推断两颗二叉树是否类似

二叉树分为 ：1、全然二叉树  2、满二叉树

结构性质：


1）.满二叉树 高度为h ，节点数则为 2^h - 1。且叶子节点全在最下层，且叶子节点数为2^（n-1）个｛n代表二叉树层数，也叫深度｝

2）.n个节点的 全然二叉树 深度为 int（log2n）（以2为底n的对数）+ 1。 

3）.非空二叉树 叶子节点个数==双分支节点数+1

4）.非空二叉树 某节点编号 n  若有左孩子，则左孩子节点 2*n，若有右孩子。则其节点编号为2*n+1

5）.知道当中两种遍历方式，就可知第三种遍历方式。

6）.推断俩颗二叉树是否同样，仅仅需推断他们随意俩种相相应的遍历顺序就可以

建树：

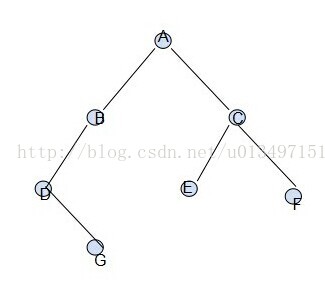
已知输入的字符为某颗二叉树的先序序列，如abcXXdeXgXXfXXX (当中X表示空节点),建立二叉树

struct node *make()
{
    char c;
    node *st;
    c = getchar();
    if(c=='X')
        st = NULL;
    else
    {
        st = (struct node *)malloc(sizeof(struct node));
        st ->data = c;//已知为先序遍历。先填充根节点
        st ->left = make();//递归形式填充左分支
        st->right = make();//递归形式填充左分支
    }
    return st;
}

遍历方式：

遍历方式非常重要，首先要知道怎样遍历，才干打出代码。如今脑海里模拟一遍

一、先序遍历
    

    1.先訪问根节点

    2.再訪问左分支

    3.再訪问右分支

上述图片二叉树的先序遍历：ABDGCEF

二、中序遍历
  
    1.先訪问左分支
    2.在訪问根节点
    3.再訪问右分支
上述图片二叉树的中序遍历：DGBAECF

三、兴许遍历

    1.先訪问左分支
    2.再訪问右分支

    3.再訪问根节点

上述图片二叉树的后序遍历：GDBEFCA

四、层次遍历

就是从每一层依照从左至右的顺序，一次遍历该层全部的节点

採用环形队列的方法，进行訪问

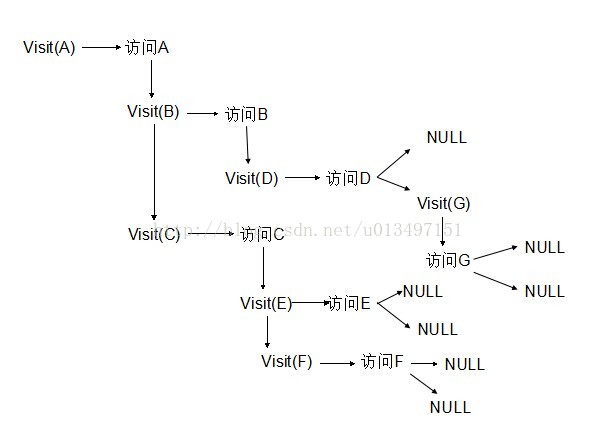
訪问叶子节点

上述递归示意图例如以下：

二叉树的深度

从当前节点的左右分支開始推断。谁大自增1

推断倆颗二叉树是否类似

1.全部节点的相应左右孩子都同样

2.如过 有随意俩种遍历方式同样，那么俩颗树就同样

代码模版：

#include <iostream>
#include <stdlib.h>
#include <stdio.h>
#include <string.h>
#include <algorithm>
const int N = 1010;
using namespace std;
char a[100];
struct node{
    char data;
    node *left;
    node *right;
};
struct node *make()
{
    char c;
    node *st;
    c = getchar();
    if(c=='X')
        st = NULL;
    else
    {
        st = (struct node *)malloc(sizeof(struct node));
        st ->data = c;//已知为先序遍历，先填充根节点
        st ->left = make();//递归形式填充左分支
        st->right = make();//递归形式填充左分支
    }
    return st;
}

void First_Order(struct node *t )//先序遍历的递归形式
{
    if(t==NULL)
        return ;
    printf("%c -> ",t->data);
    First_Order(t->left);
    First_Order(t->right);
}
void First_Order_1(struct node *t)//先序遍历非递归形式
{
    struct node *stk[N],*p;
    int top = -1;
    if(t!=NULL)
    {
        top++;
        stk[top] = t; //根节点进栈
        while(top>-1)
        {
            p = stk[top];//出栈并訪问该节点
            top--;
            printf("%c -> ",p->data);
            if(p->right!=NULL)  //右孩子进栈
            {
                top++;
                stk[top] = p->right;
            }
            if(p->left!=NULL)//左孩子进栈
            {
                top++;
                stk[top] = p->left;
            }
        }
    }
}
void Mid_Order(struct node *t)//中序遍历递归形式
{
    if(t==NULL)
        return ;
    Mid_Order(t->left);
    printf("%c -> ",t->data);
    Mid_Order(t->right);
}

void Mid_Order_1(struct node *t)//先序遍历非递归形式
{
    struct node *stk[N],*p;
    int top = -1;
    if(t!=NULL)
    {
         p = t;

        while(top>-1 ||p!=NULL )// 遍历左分支
        {
           while(p!=NULL)     // 将当前t节点的左分支。全部压入栈
           {
               top++;
               stk[top] = p;
               p = p->left;
           }
           //while结束后。栈顶元素可能没有左分支节点或者左分支节点已经訪问完成
           if(top>-1)
           {
               p = stk[top];//出栈 ，并打印
               top--;
               printf("%c -> ",p->data);
               p = p->right;  // 遍历右分支
           }
        }
    }
}

void Last_Order(struct node *t)//后序遍历递归形式
{
    if(t==NULL)
        return ;
    Last_Order(t->right);
    Last_Order(t->left);
    printf("%c -> ",t->data);
}


void Print_Leaf(struct node *t)
{
    if(t!=NULL)
    {
        if(t->left==NULL && t->right==NULL)
        {
            printf("%c  ",t->data);
        }
            Print_Leaf(t->left);//訪问左分支的叶子节点
            Print_Leaf(t->right);//訪问右分支的叶子节点
    }
}

void Ceng_Order(struct node *t)//层次遍历，採用循环队列来实现
{
    struct node *que[N],*p;
    int f,r;   //队列的头指针 和 尾指针
    f = -1; r = -1;
    que[++r] = t;  //根节点入队
    while(f!=r)
    {
        f = (f + 1)% N; //防止队溢出
        p = que[f]; //队列头结点 出队
        printf("%c -> ",p->data);
        if(p->left !=NULL)  // 将其左孩子 压入队列
        {
            r = (r + 1 )% N;
            que[r] = p->left;
        }
        if(p->right !=NULL)  // 将其右孩子 压入队列
        {
            r = (r + 1 )% N;
            que[r] = p -> right;
        }
    }
}

int shendu(struct node *t)
{
    int x=0,y = 0;
    if(t!=NULL)
    {
        x = shendu(t->left);
        y = shendu(t->right);

        if(x>y)
            return(x+1);
        else
            return (y+1);
    }
    else
        return 0;
}

/*bool Like(struct node *t1,struct node *t2)//推断俩颗树是否类似
{
    bool like1,like2;
    if(t1==NULL && t2 ==NULL)
        return true; //全部相应的分支都同样
    else if(t1==NULL || t2 ==NULL)
        return false;
    else
    {
        like1 = Like(t1->left,t2->left);
        like2 = Like(t1->right,t2->left);
        return (like1 && like2); //返回的是 like1 与 like2的 与
    }
}*/

int main()
{
    struct node *t;
    t = make();//建树

    puts("先序遍历,递归形式");
    First_Order(t);
    cout<<"END"<<endl<<endl;
    puts("非递归形式");
    First_Order_1(t);
    cout<<"END"<<endl<<endl;

    puts("中序遍历，递归形式");
    Mid_Order(t);
    cout<<"END"<<endl<<endl;
    puts("非递归形式");
    Mid_Order_1(t);
    cout<<"END"<<endl<<endl;

    puts("后序遍历，递归形式");
    Last_Order(t);
    cout<<"END"<<endl<<endl;

    puts("层次遍历");
    Ceng_Order(t);
    cout<<"END"<<endl<<endl;

  /*  puts("推断俩个二叉树是否类似");
     输入两个二叉树.....
    bool m = Like(t1,t2);
    
    if(m==1)
        printf("YES
");
    else
        printf("NO
");
    cout<<endl;*/

    puts("深度");
    int du = shendu(t);
    printf("%d
",du);
    puts("叶子节点为");
    Print_Leaf(t);
    cout<<endl<<endl;

    return 0;
}