版权声明:本文为博主原创文章,未经博主同意不得转载。 https://blog.csdn.net/gshengod/article/details/24983333
(转载请注明出处:http://blog.csdn.net/buptgshengod)
1.背景知识
前面我们提到的数据集都是线性可分的。这样我们能够用SMO等方法找到支持向量的集合。然而当我们遇到线性不可分的数据集时候,是不是svm就不起作用了呢?这里用到了一种方法叫做核函数,它将低维度的数据转换成高纬度的从而实现线性可分。
可能有的人不明确为什么低维度的数据集转换成高维度的就能够实现线性可分,以下摘抄一个网上的样例解释一下。看以下这个图,我们设红色的区域是一组数据
,而直线ab除了红色区域以外是还有一组数据。
由于直线是一维的,所以我们无法找到一条直线区分这两组数据。
单是当我们把这组数据引入二维之后。我们能够得到一组曲线,它在ab直线上部分指向黑色直线部分,ab直线下部指向红色部分。
我们通过这个样例能够看到核函数的作用,由于svm的结果仅仅跟向量内积有关系。所以我们能够配合核函数实现随意数据集的分类。
假设有人问,假设就是有一定的点数使得我们不管添加多少维度都不能实现分类,这就是引用松弛变量的意义。忽略这一部分点,由于它们非常有可能是噪声。
2.代码部分
由于核函数有非常多种类,比較经常使用的就是径向基核函数(RBF)。这个准确率是比較高的。公式:
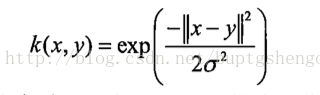
K = exp(K/(-1*kTup[1]**2))