8.7总结
得分
100+100+80
Rank 1~~
第三题可以水好多分啊
真实模拟NOIP环境
T1
题目大意

对于30%的数据,n≤10000.
对于另外20%的数据,bi=1,n≤1000000.
对于另外20%的数据,f[1]...f[k-1]=1.
对于另外20%的数据,k≤30.
对于100%的数据,1≤k≤200,1≤n≤40000000,1≤bi,fi≤998244352.
比赛的时候想了好久,打出来之后觉得是正解但是跑不过,就吸了氧。后来发现确实是正解。
正解
很明显,答案是有f[1~k]的某个次幂的乘积,即
(ans=Pi f[i]^{c[i]}|1leq i leq k)
关键怎么求c[i]。很明显是矩阵乘法优化递推。分开求每个c[i],但是转移矩阵是一样的。构建出转移矩阵的n-k次幂之后就可以求c[i]了。
时间复杂度O((k^3logn)),开O3才能过
T2
题目大意
给定n个区间,m个点。若某个区间包含某个点那它们可以配对。求最大匹配数。

也是挺好想到的吧。
正解
贪心。
显然,把点按横坐标从小到大排序,对于一个点,它与包含它的区间中右端点最靠左的那个匹配是最优的。70分get
满分的话,我们要维护包含当前点的区间的集合,还要找到右端点最小的那个。容易想到开一个堆去存。把区间按左端点从小到大排序,维护一个指针把新的包含当前点的区间扔进堆里。100分get。
T3
题目大意
有一棵n个节点的无根树,给出其中的m对点对<x,y>。问有多少条树上的简单路径<u,v>满足该路径上不存在任何一对给出的点对<x,y>。
这里我们认为路径<u,v>和<v,u>是相同的。并且对于题目中给出的点对<x,y>满足x!=y,对于你要计数的路径<u,v>满足u!=v(即单点不算答案)。
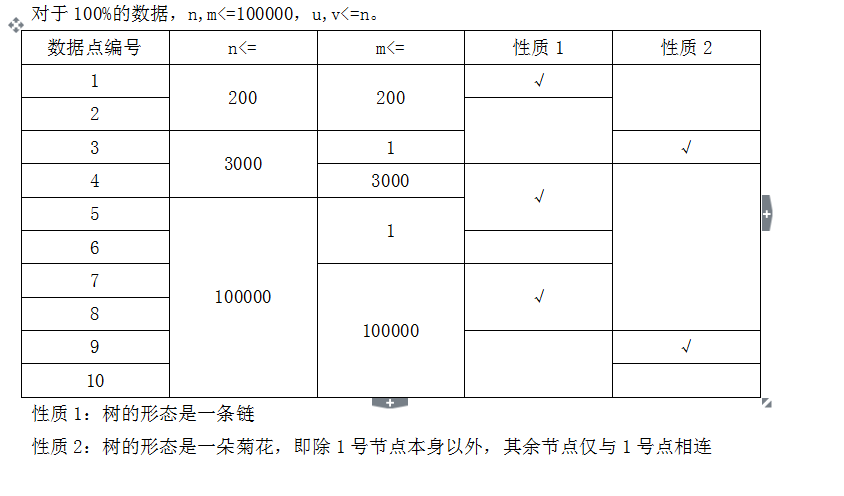
乱搞拿了80分。只有菊花图那一种没拿分。
正解
首先,这道题如果完全不会正解也是可以通过乱搞拿90分的。说一下菊花图怎么搞。有点对(1,x)时相当于删除x点,有点对(x,y)时答案只会减一。当然还要去重。
正解是求dfs序把树上问题转化为区间问题。
把dfs序求出来之后,有点对(x,y)时相当于把一个(或两个)平面上的矩形个禁掉了。分类讨论。
题目就转化为求矩形面积并。用线段树解决。每个线段树上的节点记录两个值bz被标记过几次和sum这个区间有多少个可用点。由于只用查询根节点,删除时是从加入时的对应区间删,所以很好做。不用下传标记。
小结
- 永远重视部分分,NOIP总是会给很多奇怪的部分分,拿三题的大量部分分比死刚两道题的正解要安全的多。
- 时间安排要有计划性,什么是时候做什么事,该换题就该换,不要优柔寡断导致全盘皆输