上下文无关语法

直观的理解,V变元指代一类事物,如V指代动词,那么T总结符就是一系列具体动作,初始符就是文化最开始,未发生任何变化时的样子.

产生式麻,就是动词到具体动作的映射过程

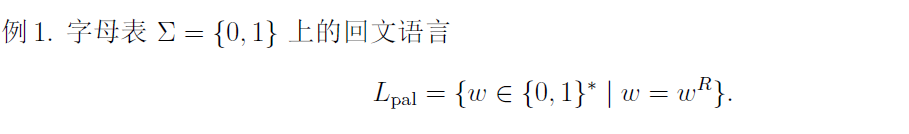
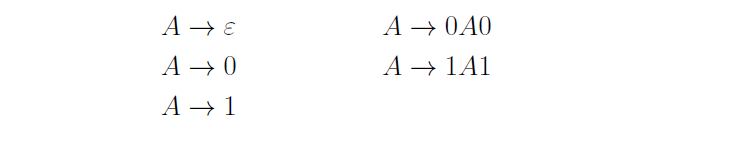
• 上下文无关文法是形式化描述语言的又一种工具;
• 它表示语言的能力强于有穷自动机和正则表达式, 但也有无法它表示的语言;
• 基本思想是用变量表示串的集合;
• 递归的使用变量去定义变量, 因此善于表示嵌套的结构, 比如匹配的括号等;
• 变量之间仅使用了“连接”, 同一变量的不同定义使用了“并”.

字符使用的一般约定

• 终结符: 0, 1, . . . , a, b, . . .
• 终结符串: . . . ,w, x, y, z
• 非终结符: S, A,B, . . .
• 终结符或非终结符: . . . ,X, Y,Z
• 终结符或非终结符组成的串: α, β, γ, . . .

归约和派生

从字符串到文法变元的分析过程, 称为递归推理(recursive inference) 或归约(reduction) ;
从文法变元到字符串的分析过程, 称为推导或派生(derivation).

• 归约: 自底向上(bottom up), 由产生式的体向头的分析
• 派生: 自顶向下(top down), 由产生式的头向体分析

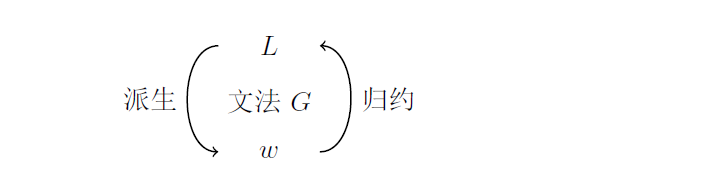
最左派生和最右派生

为限制派生的随意性, 要求只替换符号串中最左边变元的派生过程, 称为最左派生(left-most derivation),

只替换最右的, 称为最右派生(right-most derivation).

文法的语言

上下文无关是指在文法派生的每一步αAβ ⇒ αγβ, 符号串γ 仅根据A 的产生式派生, 而无需依赖A 的上下文α 和β.

文法的等价性

如果有两个文法CFG G1 和CFG G2, 满足L(G1) = L(G2), 则称G1 和G2 是等价的.

句型

• 只含有终结符的句型, 也称为G 的句子(sentence)
• 而L(G) 就是文法G 全部的句子

文法设计举例

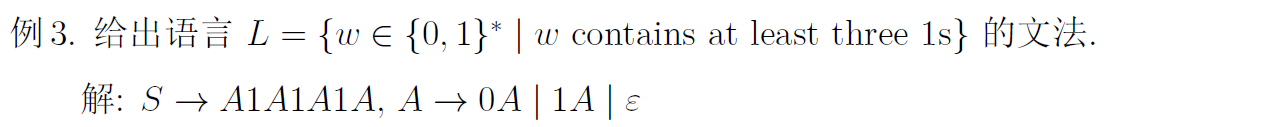
至少包含xx, 则先将xx写出来, 再用其他变元插入进行变化

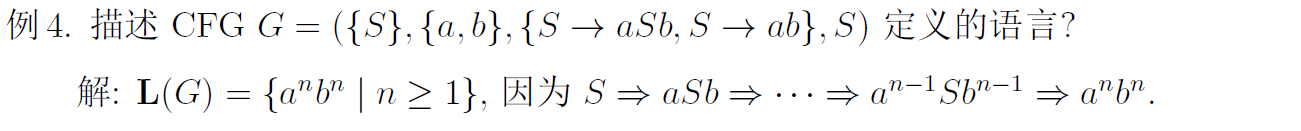
将CFG 变为正则表达式直接用P进行迭代

例4是相等的情况,不相等的情况,只需要相等情况C + 独自情况A,B即可

思考n < m的情况: 先写出相等,再加上偏移的字符

推荐解2. 当要求0,1相等,没有位置要求,则先将1,0 列出来,再插缝,注意0,1顺序的不同

先写出i = 2j的情况,再加上偏移,注意偏移的写法

语法分析树

派生或归约的过程可以表示成树形结构.

语法树和派生是等价的

语法树唯一确定最左(右) 派生

文法和语言的歧义性

定义. 如果CFG G 使某些符号串有两棵不同的语法分析树, 则称文法G 是歧义(ambiguity)的.

有些文法的歧义性, 可以通过重新设计文法来消除.

定义同样的语言可以有多个文法, 如果CFL L 的所有文法都是歧义的, 那么称语言L是固有歧义(Inherent Ambiguity) 的.

文法的化简与范式

以不改变语言为前提, 化简文法和限制文法的格式

文法的化简

1. 消除无用符号(useless symbols): 对文法定义语言没有贡献的符号
2. 消除ε 产生式(ε-productions): A → ε (得到语言L − {ε})
3. 消除单元产生式(unit productions): A → B

无用符号, 从文法开始符号派生到终结符串的过程中用不到; ε-产生式, 除了空串ε 自身,
没有贡献语言中其他的串; 单元产生式, 仅仅增加了推导(或归约) 的步骤. 这三者对语言的定
义都没有实质的作用.

消除无用符号

可达就是S可到达的变元

产生就是可以派生到全部为终结符的串的变元

计算“产生的”符号集

1. 每个T 中的符号都是产生的;
2. A → α ∈ P 且α 中符号都是产生的, 则A 是产生的

计算“可达的”符号集

1. 符号S 是可达的;
2. A → α ∈ P 且A 是可达的, 则α 中符号都是可达的.

注意

• 先寻找并消除全部非“产生的”符号
• 再寻找并消除全部非“可达的”符号
• 否则可能消除不完整

消除ε-产生式

定义. 文法中形如A → ε 的产生式称为ε-产生式.
如果变元A ⇒∗ ε, 称A 是可空的.

确定“可空变元”

1. 如果A → ε, 则A 是可空的;
2. 如果B → α 且α 中的每个符号都是可空的, 则B 是可空的.

消除单元产生式

如果有A ⇒∗ B, 则称[A,B] 为单元对.

单源产生式,即该产生式对应一个变元,而不是组合

A ==> B是单源产生式, A ==>BC不是单源产生式

同时注意,消除的只是 A ==> B,而不是B. 产生式B ==> … 依然成立

消除单元产生式

1. 删除全部形为A → B 的单元产生式;
2. 对每个单元对[A,B], 将B 的产生式复制给A.

限制文法格式

将任意形式的文法转换为:

1. 乔姆斯基范式(CNF, Chomsky Normal Form)
2. 格雷巴赫范式(GNF, Greibach Normal Form)

乔姆斯基范式

定理21 (乔姆斯基范式CNF). 每个不带ε 的CFL 都可以由这样的CFG G 定义, G 中每个产生式的形式都为

A → BC 或A → a (这里的A, B 和C 是变元, a 是终结符.)

乔姆斯基, 要么两个大人(两个变元), 要么是一个小孩(终结符)

反正成人不能单身

CFG 转为CNF 的方法

将终结符封装成变元

将一系列变元变成2个级联的形式

格雷巴赫范式

定理22 (格雷巴赫范式GNF). 每个不带ε 的CFL 都可以由这样的CFG G 定义, G 中每个产生式的形式都为

A → aα (其中A 是变元, a 是终结符, α 是零或多个变元的串.)

GNF就是一个小孩一个大人(可以没有), 两个成人不能在一起,在一起必须有小孩在前面

间接左递归可以理解为循环引用

---

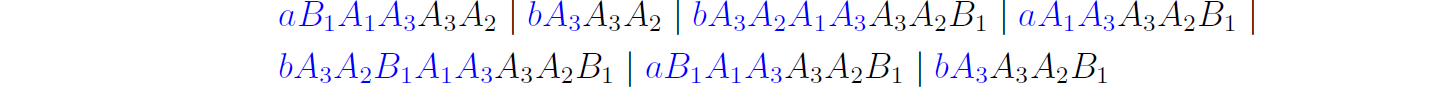
上下文无关语法的性质

上下文无关语言的泵引理

找到中间一个大小为N的块,增减其两端的字符,其任符合上下文无关语法

对比

找到前面一个大小为N的块,任意增减其末尾字符, 其仍然属于正则表达式

定理 34. 如果有 Σ 上的 CFL L 和代换 s, 且每个 a ∈ Σ 的 s(a) 都是 CFL, 那么 s(L) 也是
CFL.

定理 35. 上下文无关语言在并, 连接, 闭包, 正闭包, 同态下封闭.

定理 36. 如果 L 是 CFL, 那么 L R 也是 CFL.

CFL 对交运算不封闭

CFL 对补运算不封闭

定理 38. 若 L 是 CFL 且 R 是正则语言, 则 L ∩ R 是 CFL

根据上下文无关语言的性质判断一个语言是否是上下文无关的