图之最短路径问题(单源篇)

这篇文章用来复习最短路径问题之单源最短路径问题.
解决这个问题的算法是Dijkstra算法,他是以一个人名来命名的,老爷子是个荷兰人

可惜的是他在02年的时候去世了
他生前提出过许多很有意思的算法问题并引发了一系列的思考,包括哲学家聚餐问题,信号量PV操作等.
图灵奖当然少不了他啦.

---

使用Dijkstra解决单源最短路问题

有着近40年历史的解法是贪婪算法的最好例子,贪婪算法一般的分阶段求解一个问题,在每个阶段它都把当前出现的当作是最好的去处理.
下面用一个案例讲解一下算法流程
假定V1是被设置为了起点

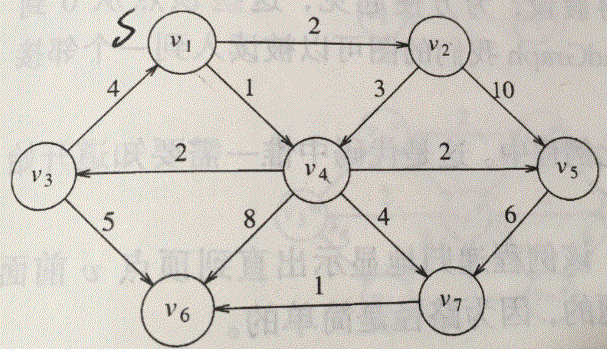
第一步初始化,从V₁点开始更新与其相邻的顶点距离.

---

V	known	dv	p v
V1	1	0	-1
V2	0	2	1
V3	0	MAXDIX	-1
V4	0	1	1
V5	0	MAXDIX	-1
V6	0	MAXDIX	-1
V7	0	MAXDIX	-1

解释一下列属性名称的含义:

• V :顶点编号
• known : 顶点访问状态,1为被访问 , 0为未被访问
• d_v : 到此顶点的距离
• p_v : 记录到达此顶点所经过的路径,存放的是编号

---

算法的流程:

在未被访问过的顶点中找到d_v最小的的顶点V_m.即V_m的d_v
之后遍历V_m的所有未被访问过的相邻点V_i,判断是否需要更新起点到达V_m的距离.
如果 d(起点,V_i) > d(起点,V_m)+ W(V_m,V_i)
　d(起点,V_i) = d(起点,V_m)+ W(V_m,V_i)
直到找不到V_m为止.W是指的权重.

所以,下一个要被遍历的点是V₄,因为它的d_v是1.
发现V₄连接着V_3/5/6/7,又都是未访问的状态.
于是判断 d(起点,V_3/5/6/7) > d(起点,V₄)+ W(V₄,V_3//5/6/7)
由于在初始化的时候d(起点,V_3/5/6/7)都是MAXDIX,以上不等式必定成立.
故这四个顶点都会被更新;
遍历完成,更新后数据如下.

---

V	known	dv	p v
V1	1	0	-1
V2	0	2	4
V3	0	3	1
V4	1	1	1
V5	0	3	4
V6	0	9	4
V7	0	5	4

接下来再在未访问的顶点中找d_v最小的顶点,即V₂
它相邻着V₄和V₅但是只能去判断V₅,因为V₄已经访问过了.
在V₅上判断 是否 d(起点,V₅) > d(起点,V₂)+ W(V₂,V₅)即判断 3 > 2 + 10 ,显然不成立.
遍历完成.
故此次V₂的访问并没有有效的更新图中的数据.

---

V	known	dv	p v
V1	1	0	-1
V2	1	2	1
V3	0	3	4
V4	1	1	1
V5	0	3	4
V6	0	9	4
V7	0	5	4

又开始寻找,找到了V₃和V₅都是符合要求,那到底选哪个呢,无所谓.
我们按照谁先被被找到就被选取的规则,选择V₃访问.
更新了起点到达V₆的值,即V₆的d_v.
再次寻找,选择V₅访问.
V₅连接着V₇,尝试更新V₇的d_v,发现不符合更新规则(5 !> 3 + 6)
故选择V₃,V₅访问后的结果如下

---

V	known	dv	p v
V1	1	0	-1
V2	1	2	1
V3	1	3	4
V4	1	1	1
V5	1	3	4
V6	0	8	3
V7	0	5	4

最后选择V₇访问,根据规则更新了V₆的d_v,最后选择V₆访问,没找到可访问的点.
算法结束;
这是最后的结果

---

V	known	dv	p v
V1	1	0	-1
V2	1	2	1
V3	1	3	4
V4	1	1	1
V5	1	3	4
V6	1	6	7
V7	1	5	4

关于初始化:

• d_v的初始化要为一个最大值.
• p_v的初始化要为一个不存在的编号,如-1;

	// 初始化顶点编号
	// 初始化顶点访问状态
	// 初始化记录路径数组
	// 初始化距离数组
	for (int i = 0;i < vertexNum;i++) 
	{
		vertexPtr[i].verIndex	= i;
		visited[i]	= NOVISIT;
		path[i]		= -1;
		distance[i] = MAXDIS;
	}

关于路径的记录:

当在判断结果为需要更新后path[V_i] = V_m
那我代码中的例子举例如下:

// 这就是Vm
int minDistanceVertex; 
	// 寻找权值最小且未被访问的顶点编号
	while ((minDistanceVertex = findMinDistanceVertex()) != -1) 
	{
		// 设置状态被访问
		setVertexState(minDistanceVertex,VISITED);
		// 开始遍历相邻点
		Node_s * node = vertexPtr[minDistanceVertex].NEXT;
		while (node)
		{
			// 若此相邻点未被访问
			if (getVertexState(node->verIndex) == NOVISIT)
			{
				// 计算更新后的距离
				int updateDis = distance[minDistanceVertex] + node->weight;
				// 判断更新后的距离是否小于现有距离
				if (updateDis < distance[node->verIndex])
				{
					// 更新现有距离
					distance[node->verIndex] = updateDis;
					// 记录当前顶点的上一个顶点编号
                    // path[Vi] = Vm
					path[node->verIndex] = minDistanceVertex;
				}
			}
			node = node->NEXT;
		}
	}

关于Dijkstra:

适用于权值为非负图的单源最短路径,整个算法过程将花费O(V²)时间查找最小值,每次更新d_v的时间是常数,而每条边最多有一次被更新,总计为O(E),因此总的运行时间为O(E+V²)=O(V²),若图是稠密,边数E=⊙(V²),其总结果只是可以忽略的线性增长,可见,算法不仅简单,而且基本上最优,就是因为它的运行时间与边数成线性关系.若图是稀疏的,边数E=⊙(V),那么就太慢了,在这种情况下,d_v需要存储在优先队列中,最佳的是使用斐波那契堆,使用这种数据结构的运行时间是O(E+V log(V)),具有良好的理论时间界,但是它需要相等数量的系统开销.

使用场景:

• 在一些诸如计算机邮件和大型公交传输的典型问题中,大多数顶点只有几条边,故在许多应用中使用优先队列来解决这种问题是很重要的,目前,尚不清楚在实践中是否使用斐波那契堆比使用具有二叉堆的Dijkstra算法更好.所以这种问题没有一个平均情形时间结果.

其他:

• 在我使用了邻接表存储图并且没有使用优先队列遍历的实现中,我需要的变量:

	// 记录距离的数组
	int * distance;
	// 记录路径的数组
	int * path;
	// 记录顶点访问状态
	VISITEDSTATE * visited;

总结:

　　学习了贪婪算法的思想

代码中接口部分和前面复习的图的遍历基本保持一致.
详细请见我的github.