编程练习（一）201301 JAVA题目0-1级

编写一个函数，传入一个int型数组，返回该数组能否分成两组，使得两组中各元素加起来的和相等，并且，所有5的倍数必须在其中一个组中，所有3的倍数在另一个组中（不包括5的倍数），能满足以上条件，返回true；不满足时返回false。

方法一：暴力求解

while 1:
    try:
        n = input()
        l = input().split() # 列表
        sum1 = sum2 = 0
        ll = [] # 保存 3，5 之外的数
        for i in l:
            if int(i) % 5 == 0:
                sum1 += int(i)
            elif int(i) % 3 == 0:
                sum2 += int(i)
            else:
                ll.append(int(i))
        d_value = abs(sum1 - sum2) # 2*x + d_value = sum(ll) ===> d_value = sum(ll) - 2 * x
        if not ll and d_value == 0:
            print ('true')
        elif not ll and d_value != 0:
            print ('false')
        else: # 存在差值，并且有剩余数字
            s = set()
            for x in ll:
                tmp = list(s)
                for y in tmp:
                    s.add(x + y)
                s.add(x)
            for may_value in s:
                if d_value == abs((sum(ll) - may_value) - may_value):
                    print ('true')
                    break
            else:
                print ('false')
    except:
        break

解析：首先得到 sum1, sum2，剩下的数字组成的列表ll, 以及二者的差值。如果成立，则存在x使得： 2*x + d_value = sum(ll)。即
d_value = sum(ll) - 2 * x。最朴素的方法，找到列表ll中所有数字和所有可能的值，然后代入比较。
所以问题转换为如何求一个数组中所有数字求和得到的值。

list_ = [1,2,3,4,5,6,7,5,3,2,1,5,99]
s = set()
for x in list_:
    tmp = list(s)
    for y in tmp:
        s.add(x +y)
    s.add(x)
print(s)

s 的值 {x1,x1+x2,x2,x1+x3,x1+x2+x3,x2+x3,x3......}
方法二：递归

def search(ll, target):
    if target == 0:
        return True
    if not ll:
        return False
    return search(ll[1:],target) or search(ll[1:],target - ll[0])
 
 
while True:
    try:
        m,ls = int(input()),list(map(int, input().split()))
  
        ls1 = []
        ls2 = []
        ls3 = []
 
 
        for i in ls:
            if i%5 == 0:
                ls1.append(i)
            elif i%3 ==0:
                ls2.append(i)
            else:
                ls3.append(i)
        t = abs(sum(ls1)-sum(ls2))
        d = sum(ls3) - t
        if d%2 != 0:
            print('false')
        else:
            if search(ls3,d/2):
                print('true')
            else:
                print('false')
    except:
        break

解题思路：先按提干要求构建ls1和ls2，计算ls1和ls2总和之差的绝对值t，用ls3抹平两者差距；
问题变成了：ls3的总和减去t之后的值d，d能否被ls3中元素平分。如果d是奇数，那么一定不能平分。
如果d是偶数，那么变了成能不能从ls3中挑选出若干元素，他们的和为d/2,与打靶问题有类似之处;
但是本题比打靶问题简单，打靶问题每次射击的结果从0到10有11种情况，本地只有两种情况
分解子问题：
使用递归开始查找，对ls3中的每个元素遍历，每个元素都分两种情况：参与构建d/2和不参与构建d/2;
形成一个二叉树，记录查找结果;
边界条件：
1.如果target为0了，那么说明找到了一个构建d/2的方法
2.如果ls3都查找完了还没有找到，说明没有办法构建d/2

另一种思考方式：
5的倍数一组,和为s5,3的倍数一组,和为s3,剩余的元素为一组,s5和s3相差s,
剩余的一组分成的两组之间也应该相差s才能使得最后s3组和s5组和结果相同.
假设剩余的一组和为s0,分成两组s1和s2,且s1和s2相差s,那么有s1+s2=s0且s1-s2=s;
则有s2=(s0-s)/2,s1=(s0+s)/2,因此可以转化为从剩余的一组中看是否能够找到几个数的和为s1或s2*/
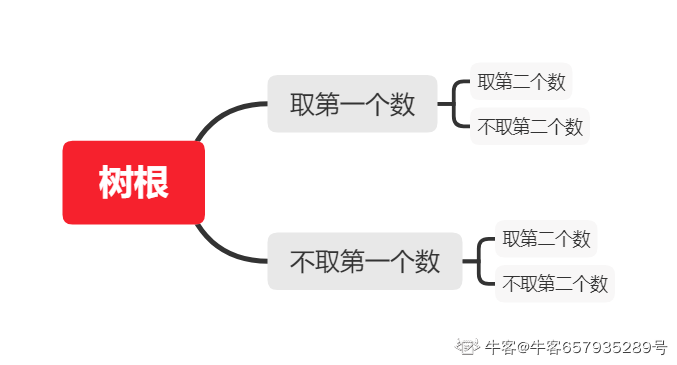
用二叉树遍历所有结果(中间能找到s1或者s2就停止),二叉树的建立就是把所有结果列出来,第一个数有取和不取两种可能,取第一个数,那么第二个数又有取和不取两种可能,不取第一个数的话,第二个数也是有取和不取两种可能.这样一直遍历查找下去,找不到就输出false.