维特比算法之中文分词

维特比原理

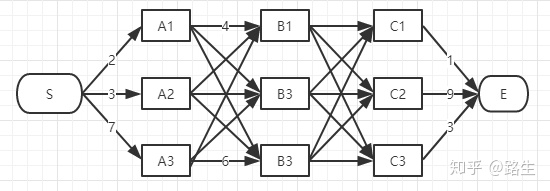
寻找上图最短路径

中文分词

此项目需要的数据：

综合类中文词库.xlsx： 包含了中文词，当做词典来用
以变量的方式提供了部分unigram概率word_prob
举个例子： 给定词典=[我们 学习 人工 智能 人工智能 未来 是]， 另外我们给定unigram概率：p(我们)=0.25, p(学习)=0.15, p(人工)=0.05, p(智能)=0.1, p(人工智能)=0.2, p(未来)=0.1, p(是)=0

1. 获取中文字典
   在变量word_prob没有出现的的单词但是出现在词典里的，统一把概率设置成为0.00001

import xlrd
file_path = './data/综合类中文词库.xlsx'
workbook = xlrd.open_workbook(file_path)
booksheet = workbook.sheet_by_index(0)
col_values = booksheet.col_values(0)
dic_words = {}
max_len_word = 0
for word in col_values:
    dic_words[word] = 0.00001
    len_word = len(word)
    if len_word > max_len_word:
        max_len_word = len_word
word_prob = {"北京": 0.03, "的": 0.08, "天": 0.005, "气": 0.005, "天气": 0.06, "真": 0.04, "好": 0.05, "真好": 0.04, "啊": 0.01,
             "真好啊": 0.02,
             "今": 0.01, "今天": 0.07, "课程": 0.06, "内容": 0.06, "有": 0.05, "很": 0.03, "很有": 0.04, "意思": 0.06, "有意思": 0.005,
             "课": 0.01,
             "程": 0.005, "经常": 0.08, "意见": 0.08, "意": 0.01, "见": 0.005, "有意见": 0.02, "分歧": 0.04, "分": 0.02, "歧": 0.005}

for key, value in word_prob.items():
    dic_words[key] = value

2. 根据词典，输入的句子和 word_prob来创建带权重的有向图（Directed Graph）

#从头开始遍历，找到字典中存在的所有候选词
def create_graph(input_str):
    N = len(input_str)
    graph = {}
    for idx_end in range(1, N + 1):
        print('idx_end',idx_end)
        temp_list = []
        max_split = min(idx_end, max_len_word) # 最大切分长度为idx_end,即这次循环的结果
        for idx_start in range(idx_end - max_split, idx_end): # 就是 0 : idx_end
            
            word = input_str[idx_start:idx_end] # 根据起止索引得到单词
            print('idx_start',idx_start, word)
            if word in dic_words:
                print(idx_start,word)
                temp_list.append(idx_start)
       
        
        graph[idx_end] = temp_list
        print(graph)
        print('_______________')
    return graph

3. 通过加权有向图，实现维特比算法
   

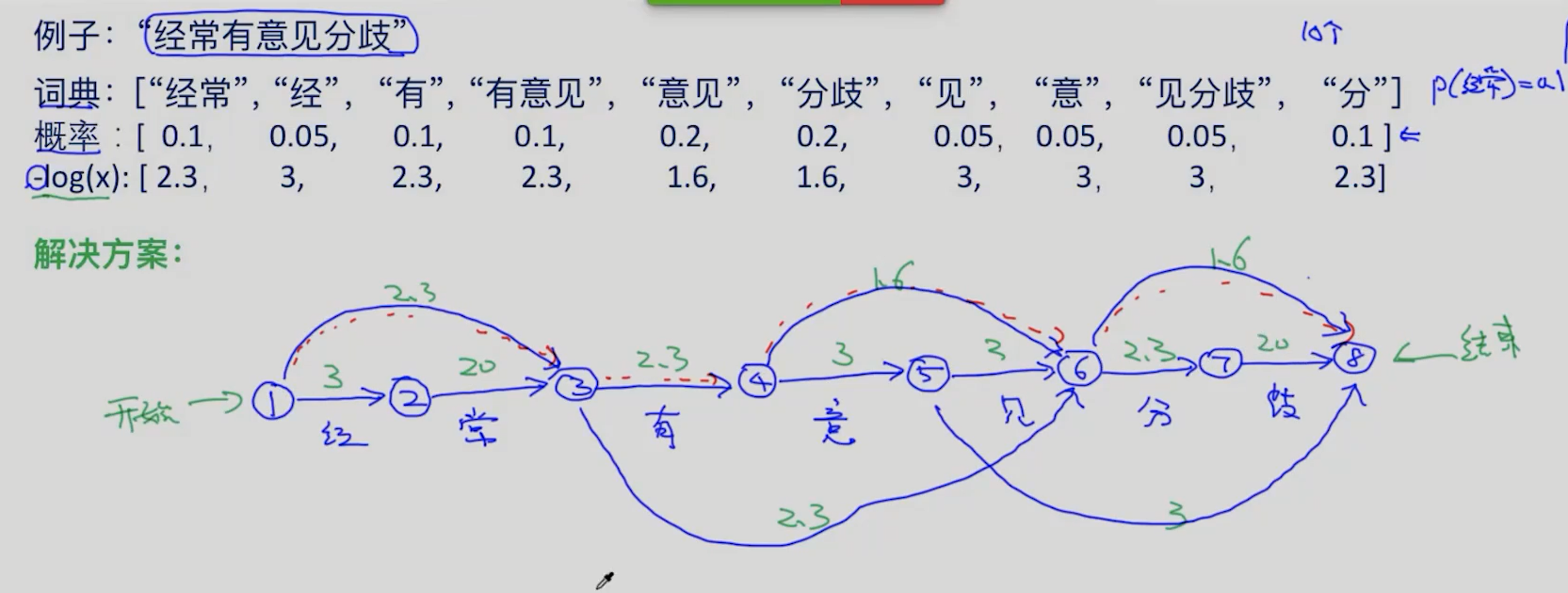
节点的含义：节点代表了它前面的那个字。
边的含义： -log(概率) 由概率最大，变为该值最小，转换为求最短距离问题

def word_segment_viterbi(input_str):
    graph = create_graph(input_str)
    N = len(input_str)
    m = [np.inf] * (N + 1) # 长度为 N+1 长度的数组。初始化无穷大。
    m[0] = 0  # 路径值，第0个节点的值为0，后面计算节点1路径权值时候，需要加上节点0的值。
    last_index = [0] * (N + 1)# 保存一路转移的索引
    for idx_end in range(1, N + 1): # 两层for循环 idx_end 为 incoming_links，字典的键
        for idx_start in graph[idx_end]: # idx_start 到 idx 组成了一个单词。input_str[idx_start:idx_end] 在字典里存在。
            # 从字典找到这个单词的概率。
            # m[idx_start] 保存了到这个单词为止，最短路径值。
            log_prob = round(-1 * np.log(dic_words[input_str[idx_start:idx_end]])) + m[idx_start]
            if log_prob < m[idx_end]:# 这次循环里，判断到idx_end 位置的最短路径值。
                m[idx_end] = log_prob
                last_index[idx_end] = idx_start
    best_segment = []
    i = N
    while True:
        best_segment.insert(0, input_str[last_index[i]:i])
        i = last_index[i]
        if i == 0:
            break
    return best_segment