JZOJ.4724 斐波那契

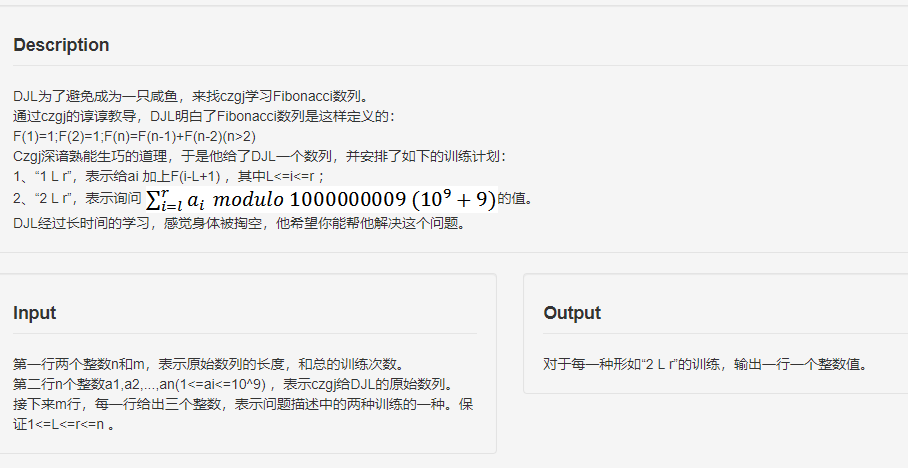
( ext{Problem})

( ext{Solution})

( ext{Fibonacci}) 数列有一个性质：若 (H_1=a，H_2=b，H_n=H_{n-2}+H_{n-1})
则有 (H_n=acdot F_{n-2}+bcdot F_{n-1})

有了这个性质后，对一段区间加斐波那契数列后，我们可以 (O(1)) 知道任意一位加的数是多少（当然是预处理出斐波那契数列后）
也就是说维护这段区间前两位加的数 ({a，b}) 即可
对于一段区间求区间和即 (ans=acdot[(sum_{i=1}^{r-l-1}F_i)+1]+bcdotsum_{i=1}^{r-l}F_i)
线段树维护每段区间加的 (a，b) 即可

( ext{Code})

#include<cstdio>
#define ls (p << 1)
#define rs (ls | 1) 
typedef long long LL;
using namespace std;

const int N = 1e5 + 5;
const LL P = 1e9 + 9;
int n, m;
LL a[N], F[N], sF[N];
LL sum[N * 4], tg1[N * 4], tg2[N * 4];

void pushup(int p) {sum[p] = (sum[ls] + sum[rs]) % P;} 
void update1(int l, int r, int p, int x, int v)
{
	if (l == r) return void(tg1[p] = sum[p] = v);
	int mid = (l + r) >> 1;
	if (x <= mid) update1(l, mid, ls, x, v);
	else update1(mid + 1, r, rs, x, v);
	pushup(p);
}
void change(int l, int r, int p, LL v1, LL v2)
{
	sum[p] = (sum[p] + v1 * (sF[(r - l - 1)<0?0:(r - l - 1)] + 1) % P + v2 * sF[r - l] % P) % P;
	tg1[p] = (tg1[p] + v1) % P, tg2[p] = (tg2[p] + v2) % P;
}
void pushdown(int l, int r, int p)
{
	if (!tg1[p] && !tg2[p]) return;
	int mid = (l + r) >> 1;
	change(l, mid, ls, tg1[p], tg2[p]);
	LL v1 = (tg1[p] * F[mid - l] % P + tg2[p] * F[mid - l + 1] % P) % P;
	LL v2 = (tg1[p] * F[mid - l + 1] % P + tg2[p] * F[mid - l + 2] % P) % P;
	change(mid + 1, r, rs, v1, v2);
	tg1[p] = 0, tg2[p] = 0;
}
void update2(int l, int r, int p, int x, int y, LL v1, LL v2)
{
	if (x <= l && r <= y) return void(change(l, r, p, v1, v2));
	int mid = (l + r) >> 1;
	pushdown(l, r, p);
	if (x <= mid) update2(l, mid, ls, x, y, v1, v2);
	LL a = v1, b = v2;
	if (l <= x && x <= mid) a = (v1 * F[mid - x] % P + v2 * F[mid - x + 1] % P) % P,
				b = (v1 * F[mid - x + 1] % P + v2 * F[mid - x + 2] % P) % P;
	else if (l > x && x <= mid) a = (v1 * F[mid - l] % P + v2 * F[mid - l + 1] % P) % P,
		 b = (v1 * F[mid - l + 1] % P + v2 * F[mid - l + 2] % P) % P;
	if (y > mid) update2(mid + 1, r, rs, x, y, a, b);
	pushup(p);
}
LL query(int l, int r, int p, int x, int y)
{
	if (x <= l && r <= y) return sum[p];
	int mid = (l + r) >> 1; LL ret = 0;
	pushdown(l, r, p);
	if (x <= mid) ret = query(l, mid, ls, x, y);
	if (y > mid) ret = (ret + query(mid + 1, r, rs, x, y)) % P;
	return ret;
}

int main()
{
	scanf("%d%d", &n, &m);
	for(int i = 1, x; i <= n; i++) scanf("%d", &x), update1(1, n, 1, i, x);
	F[1] = 1, F[2] = 1, sF[1] = 1, sF[2] = 2;
	for(int i = 3; i <= n; i++) F[i] = (F[i - 1] + F[i - 2]) % P;
	for(int i = 3; i <= n; i++) sF[i] = (sF[i - 1] + F[i]) % P;
	for(int op, l, r; m; --m)
	{
		scanf("%d%d%d", &op, &l, &r);
		if (op == 1) update2(1, n, 1, l, r, F[1], F[2]);
		else printf("%lld
", query(1, n, 1, l, r));
	}
}