关于矩阵

打算把一些零碎的矩阵知识总结在这里，因为发现自己记的太零散，不成体系。

1、矩阵的奇异值分解（Singular Value Decomposition）

    奇异值分解是矩阵分析中正规矩阵酉对角化的推广。设矩阵A是m×n的秩为r，它的奇异值是指n阶方阵A^HA（或m阶方阵AA^H）的正特征值的平方根 (A^H是A的共轭转置)。

    奇异值分解是指如下形式的分解：

补充：酉矩阵是实数域中正交矩阵在复数域中的推广，相类似的还有共轭转置^H与实数域中的转置^T。酉矩阵的定义为方阵U满足：U^HU=UU^H=I_n

特征分解（Eigendecomposition），又称谱分解（Spectral decomposition）是将矩阵分解为由其特征值和特征向量表示的矩阵之积的方法。只有对可对角化（Diagonalizable）矩阵或有n个线性无关的特征向量的矩阵才可以施以特征分解。不是所有的矩阵都可以特征分解，其充要条件为n阶方阵存在n个线性无关的特征向量。(Diagonalizable=The eigenvectors of a matrix A can form a basis for Rⁿ)

半正定矩阵，有如下三个性质：

　　对称矩阵一定n个线性无关的特征向量
　　半正定矩阵的特征值一定非负
　　对阵矩阵的不同特征值对应的特征向量相互正交，这些正交的特征向量构成的矩阵为正交矩阵。

2：对于任意的矩阵A，AA^H一定是半正定矩阵，其特征值a_i都是非负实数。

     此时A的奇异值s_i为a_i的正平方根（半正定矩阵的特征值和奇异值相同）。（这里说明任意矩阵的奇异值均是非负实数，即奇异值一定大于等于0）。

     此时提醒我们，判断一个实对称矩阵是否正定或半正定时，要通过特征值判断，因为奇异值都是非负的。

3：什么时候一个矩阵的奇异值与特征值相同？，正如上面所述，当一个矩阵A为对称半正定矩阵时。

4：矩阵的核范数nuclear norm：||A||_*，其定义为矩阵A的奇异值之和。 由于一个矩阵的非零奇异值的个数等价于该矩阵的秩，那么此时核范数可以来近似矩阵的秩（等价于向量的0范数和1范数关系，稀疏优化），这也是常见的约束矩阵低秩的方法。

5：矩阵的迹trace：tr(A)，为矩阵主对角元素的和，同时也是矩阵所有特征值的和。

6、||A||_F为Frobenius范数，定义为矩阵A各项元素的绝对值平方和，再开根号。

 

7、谱半径

复数域方矩阵A=(a_ij)_n×n,的特征值为λ₁,…,λ_n，谱半径的定义为特征值绝对值的最大值：

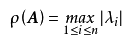
复数域上的任一n阶方阵A=(a_ij)_n×n, 的谱半径都不超过A的范数||A||（任意矩阵范数），即：

核范数的导数：