KMP算法
是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt提出的,因此人们称它为克努特—莫里斯—普拉特操作(简称KMP算法)。
KMP算法的核心是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现,函数本身包含了模式串的局部匹配信息。
KMP算法的时间复杂度O(m+n)。
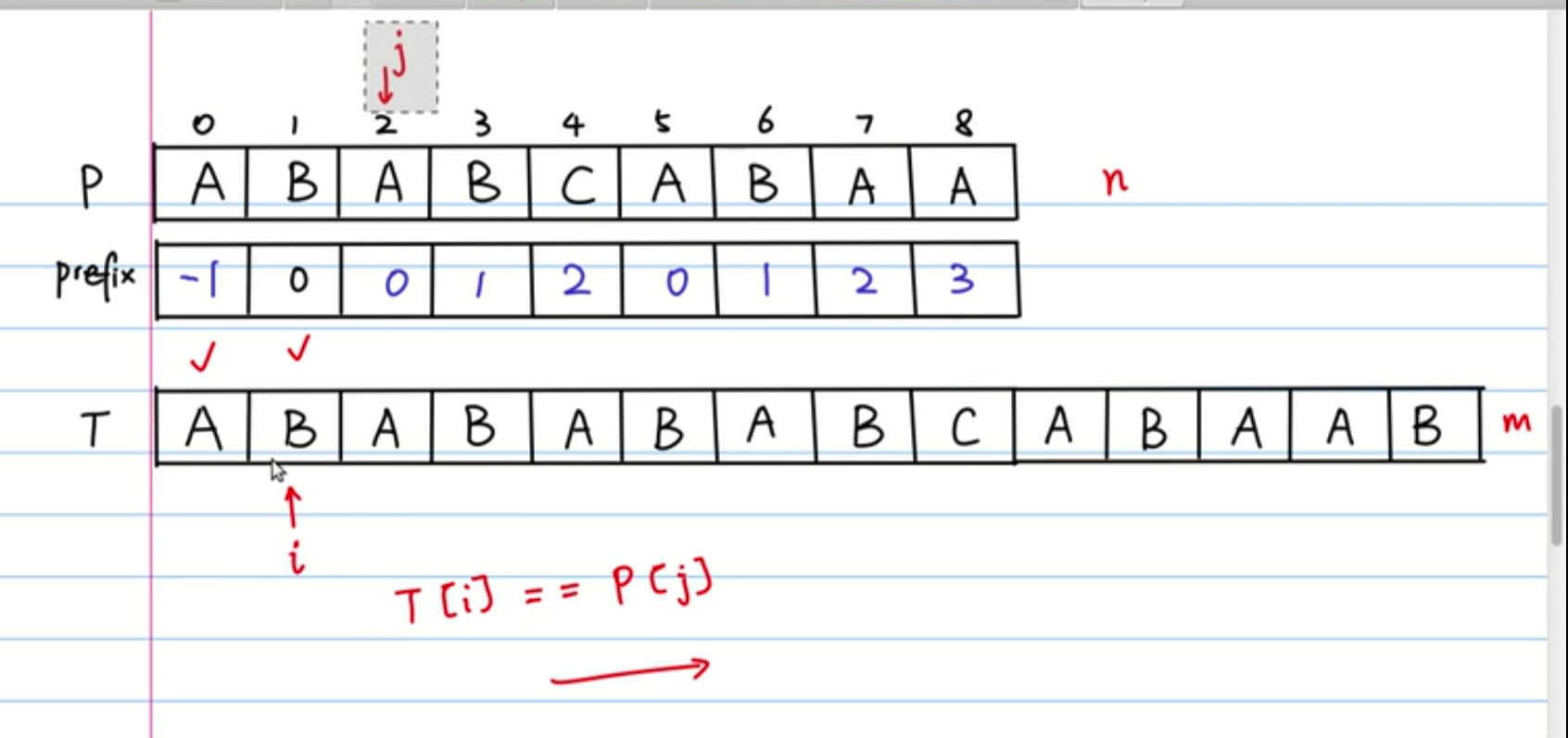
1、next[ ]数组的计算:
每个字串的:前缀子串和后缀字串的最大相同字符长度。然后整体左移一位,最开始写next[0]= -1;
模式串为:a b a c a b;
a 没有字串: 0
a b [a ] , [b ] : 0
a b a [a , ab] , [ba, a] : 1
a b a c [a, ab, aba] , [bac, ac, c]: 0
a b a c a [a, ab, aba, abac], [baca, aca, ca, a]: 1
a b a c a b 移位覆盖,不用计算:
| 模式串 | a | b | a | c | a | b |
| next[ ] | 0 | 0 | 1 | 0 | 1 |
左移:
| 模式串 | a | b | a | c | a | b |
| next[ ] | -1 | 0 | 0 | 1 | 0 | 1 |
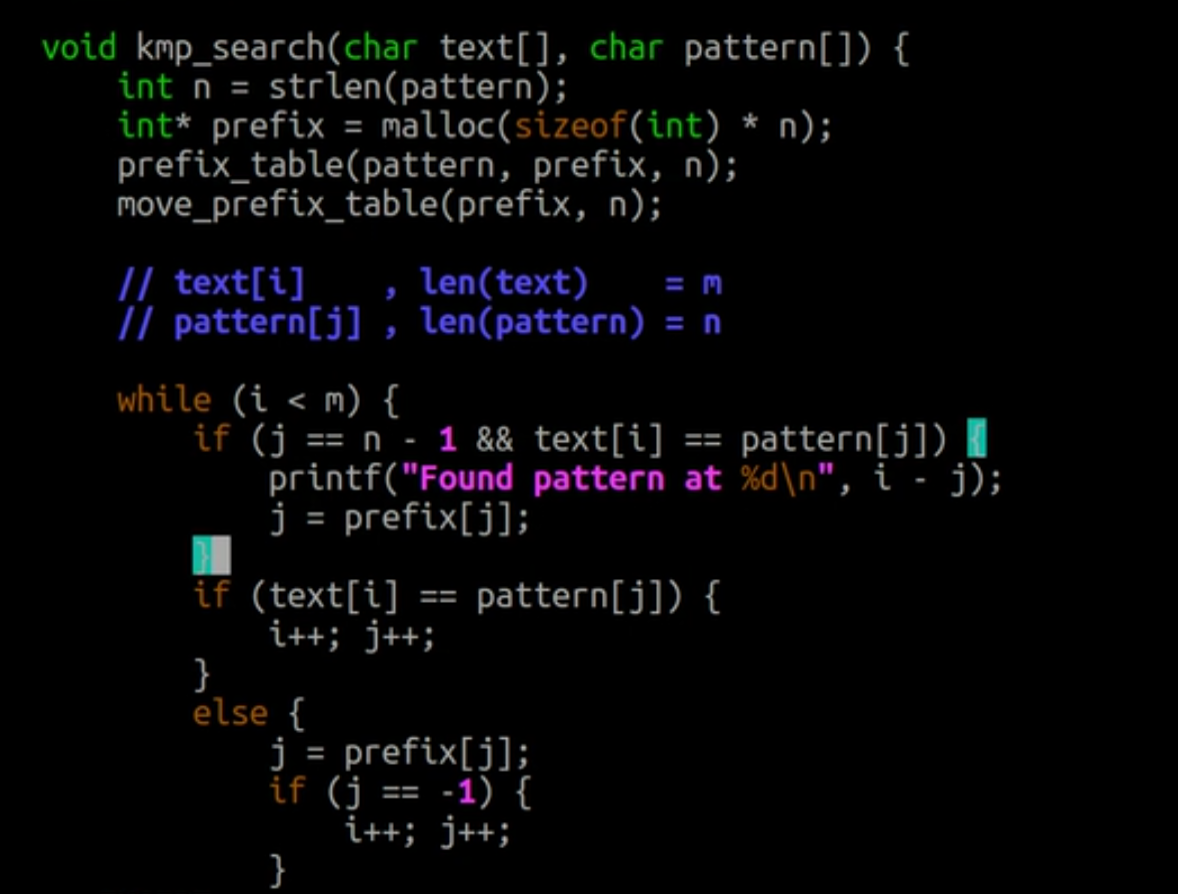
计算next数组的程序:len表示当前的最大匹配长度,i为滑动游标,进行一个一个的比较。当不相等时,需要比较len=prefix[len-1];考虑出现len-1为负数的情况,要做判断,当len==0时,直接赋值并i++;

然后需要移位。