经典的损失函数:
①交叉熵(分类问题):判断一个输出向量和期望向量有多接近。交叉熵刻画了两个概率分布之间的距离,他是分类问题中使用比较广泛的一种损失函数。概率分布刻画了不同事件发生的概率。
熵的定义:解决了对信息的量化度量问题,香农用信息熵的概念来描述信源的不确定度,第一次用数学语言阐明了概率与信息冗余度的关系。



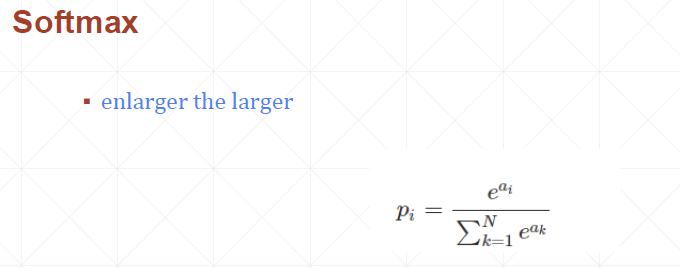
从统计方面看交叉熵损失函数的含义:


Softmax:原始神经网路的输出被作用在置信度来生成新的输出,新的输出满足概率分布的所有要求。这样就把神经网络的输出变成了一个概率分布,从而可以通过交叉熵来计算预测的概率分布和真实答案的概率分布之间的距离。
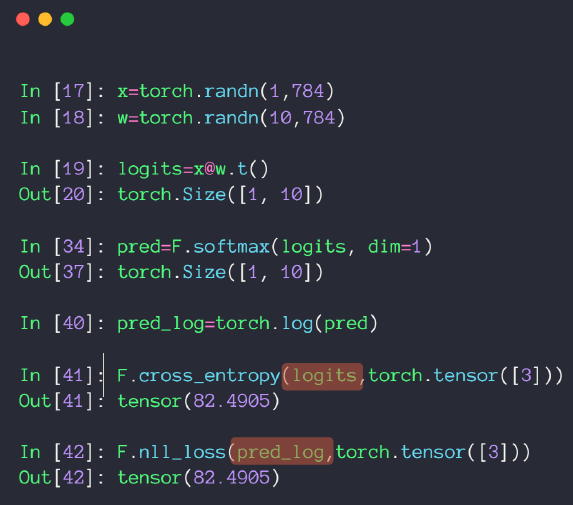
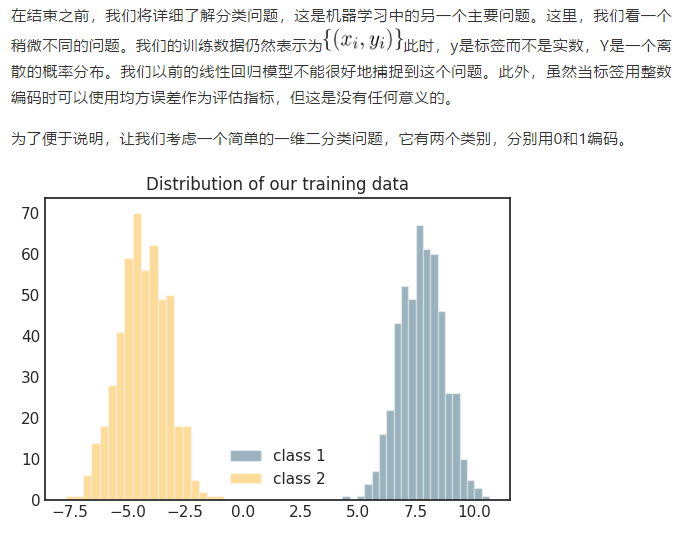
②回归问题解决的是对具体数值的预测。这些问题需要预测的不是一个事先定义好的类别,而是一个任意的实数。解决回归问题的神经网络一般只有一个输出结点,这个结点的输出值就是预测值。对于回归问题,最常用的损失函数就是均方误差(MSE,mean squared error):