B 先引入一段代码:
1 int cal(int n) { 2 int ret = 0; 3 int i = 1; 4 for (; i < n; ++i) { 5 ret = ret + f(i); 6 } 7 } 8 9 int f(int n) { 10 int sum = 0; 11 int i = 1; 12 for (; i < n; ++i) { 13 sum = sum + i; 14 } 15 return sum; 16 }
对于cal函数,只看执行次数最多的4~6行代码,负责一共执行了2n次,可对于f函数内部也执行了2n次,那么总的时间复杂度就是:T(n)= O(cal(n)* f (n)= O(4n^2)= O(n^2)。
时间和空间复杂度用来度量程序的运行时间效率和占用空间大小,即大O表示法:T(n) = O(f(n)),最终求得的时间复杂度,需要省略掉表达式中的系数、低阶、常量,因为我们只关心占用时间和空间最大的那一部分代码。
几种常见的时间复杂度量级:

这里主要分析一下对数阶复杂度,这样一段代码:
1 i=1; 2 while (i <= n) { 3 i = i * 2; 4 }
变量i从1开始取值,每次循环乘以2,得出2^x=n,根据对数公式,x = log2^n,忽略掉对数底,则时间复杂度为O(logn)。
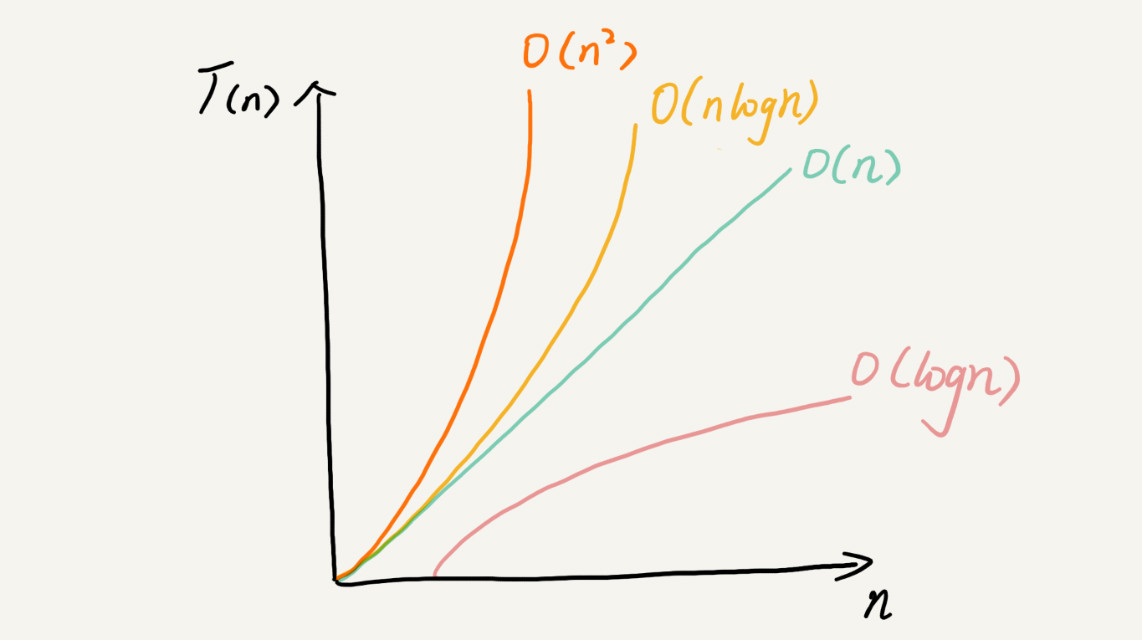
时间复杂度的全称是渐进时间复杂度,表示算法的执行时间与数据规模之间的增长关系,那么空间复杂度就是表示算法的存储空间和数据规模之间的存储关系。空间复杂度的分析只要计算出是否持续的申请内存就好,常见的空间复杂度是O(1)、O(n)、O(n^2)。越高阶复杂度的算法,执行效率越低,从小到大依次是:O(1)、O(logn)、O(n)、o(nlogn)、o(n^2) ,对应图像: