集合及其运算
集合的概念
集合包括有穷集合、无穷集合和空集。
子集、集合的相等
集合的运算
并运算
交运算
分配律
抽象
差运算
对称差
对称差与异或
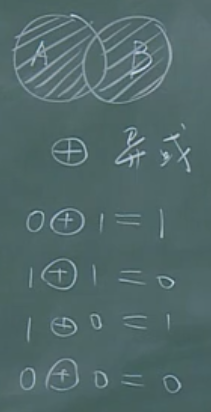
对称差定义

对称差的运算律
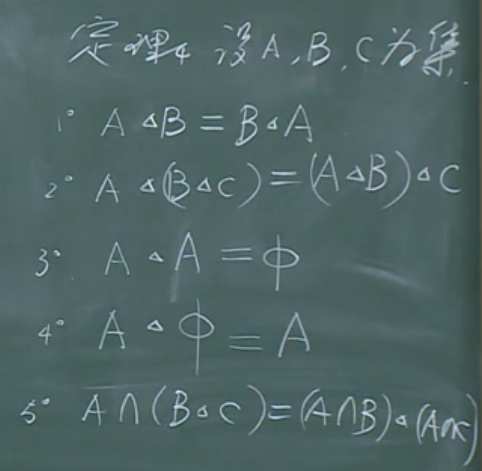
例题:
【例1】

补集、De Morgan公式
De Morgan公式
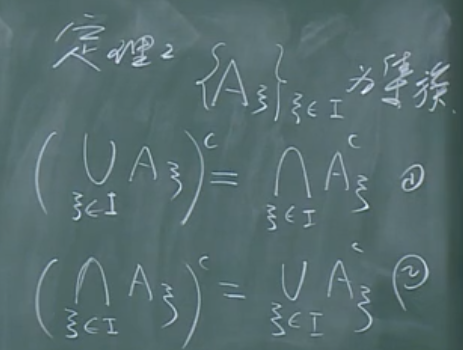
对偶原理
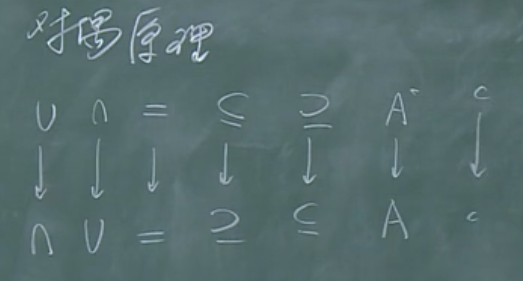
按照这个原则替换后的集合表达式,仍然成立。
运算的总结
(cup cap setminus ^C)
假设研究对象是集合S,那么
-
他们是在集合S的幂集(2^S)上的运算。
-
这些运算是封闭的(运算对象在(2^S)中,运算结果也在(2^S)中)。
幂集运算
幂集运算是不封闭的。
下面所描述的笛卡尔积也是不封闭的。
笛卡尔积/直积
笛卡尔
哲学上:《方法导论》
数学上:笛卡尔坐标系(平面直角坐标系)。数形结合,将几何形状公式化。
有序对与笛卡尔积
序偶/有序对:

【定义1】抽象集合上的笛卡尔积定义
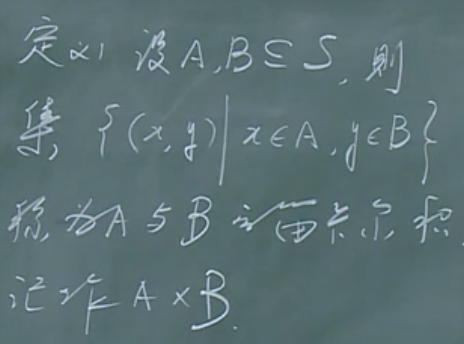
定义:

运算规律与n元组
不满足结合律与分配律

不满足结合律,分配律。
那么,(A imes B imes C)没有意义(不能这样表示)。
由于在这种情况下(A imes B imes C)没有意义,为了对多个集合作笛卡尔积运算,需要引入n元组的概念。
n元组与扩展的(n个集合的)笛卡尔积
n元组:
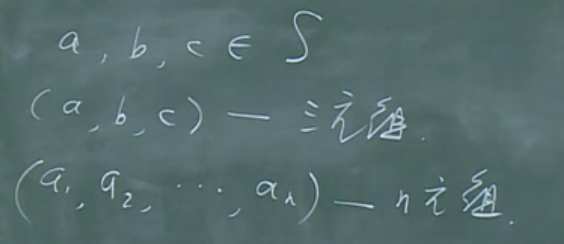
扩展的笛卡尔积:
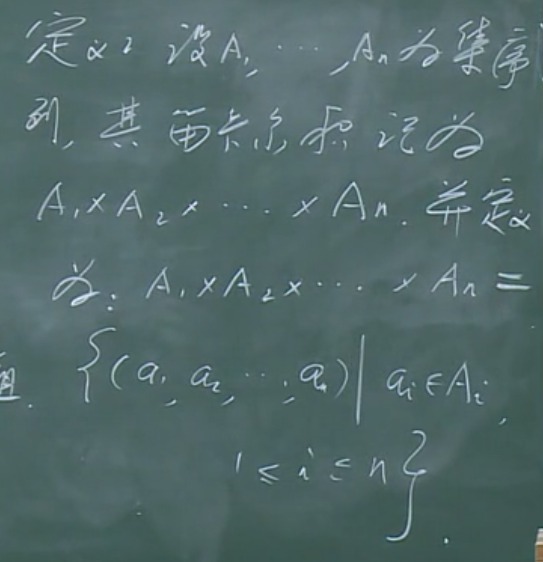
部分条件下满足分配律
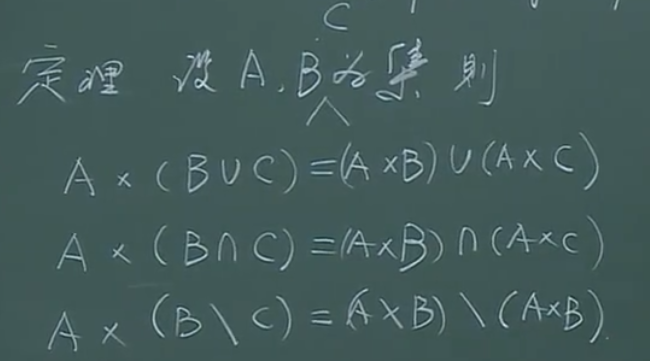
笛卡尔乘积在(2^S)上不封闭,也即产生了新的结构。
例子:冒领养老金
多种不同的数据库(如公安数据、社保数据和医院数据等等),各数据库(笛卡尔乘积有意义的子集)之间可能存在不一致性。
进行笛卡尔乘积运算并进行限定,得到的新数据库(集合)R。
但是,笛卡尔乘积是一个复杂的运算。
抽象训练
数据库模型
E-R图:(以学生和课程为例)

关系数据库:(所有的联系均可用二维关系表表示)E.F.Codd
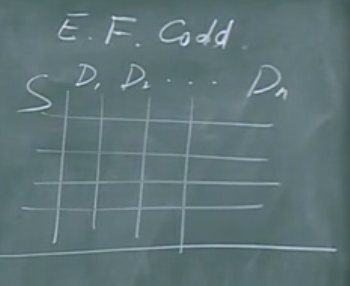
上述笛卡尔积的一个子集就是关系。
具体的关系只需要给这个子集赋值即可。
自然语言的模型
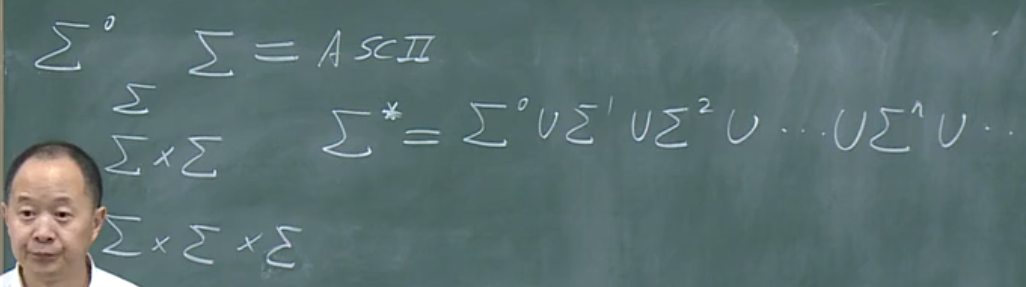
语言的生成与识别:(Chomsky的文法(产生)与Kleene的自动机(识别))

文法与自动机事实上是等价的。
语言的分类:
0型:短语结构语言(PSG)、图灵机
1型:上下文有关语言(CSG)、线性界限自动机
2型:上下文无关语言(CFG)、下推自动机
3型:正则语言、自动机(RG)
映射与一一对应
映射概念

注意:映射是一个单值联系(体现在其唯一性上)。
映射的三种分类
单射
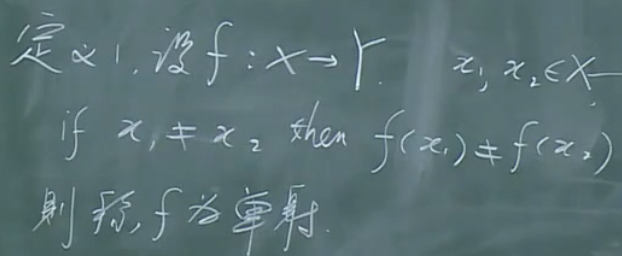
满射
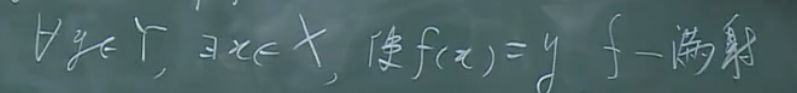
双射(一一对应)

注意:如果两个集合之间具有一一对应的关系,那么可以将这两个集合视为一类。
可以用一一对应来定义等价关系。
有穷集合的基数
【定义】
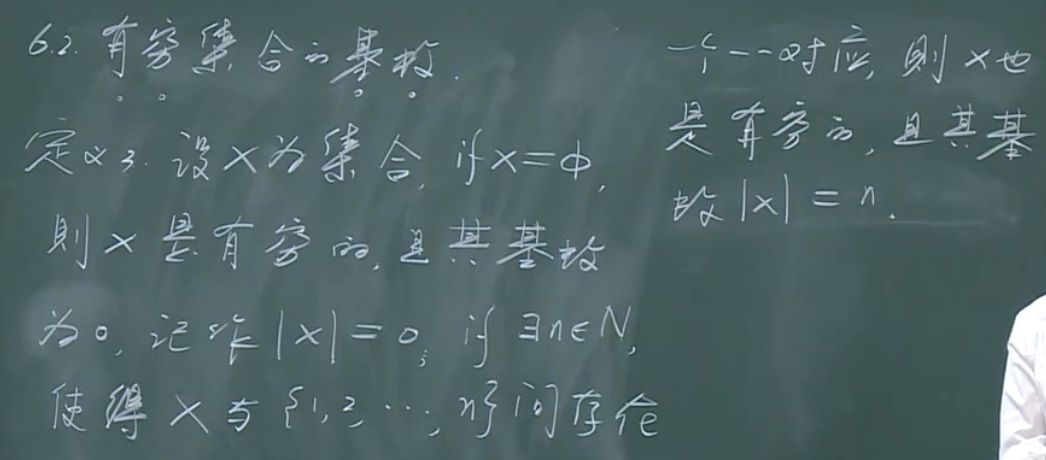
计数法则
简单法则
当(Acap B=varnothing)时:
包括加法法则、乘法法则、
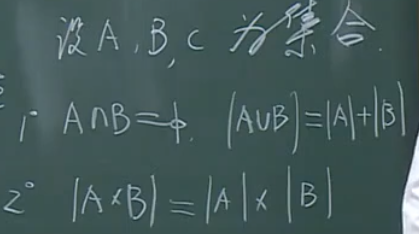
减法法则(可用补运算转化为加法运算)。
当不满足(Acap B=varnothing)时呢?
容斥原理(逐步淘汰原理)
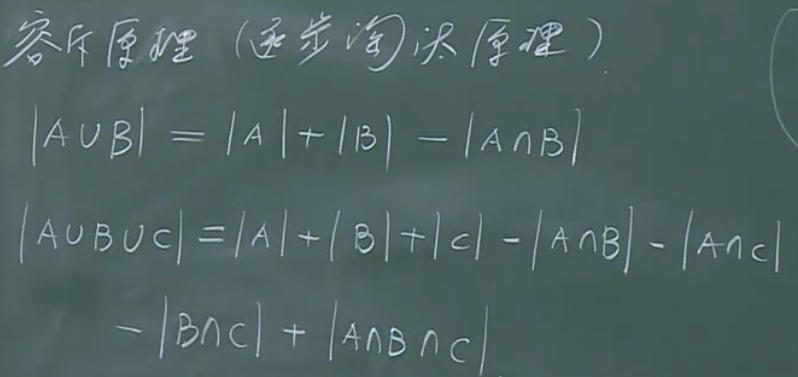
映射
映射的概念
鸽巢原理
定理
桌上有十个苹果,要把这十个苹果放到九个抽屉里,无论怎样放,我们会发现至少会有一个抽屉里面放不少于两个苹果。这一现象就是我们所说的“抽屉原理”。
抽屉原理的一般含义为:“如果每个抽屉代表一个集合,每一个苹果就可以代表一个元素,假如有n+1个元素放到n个集合中去,其中必定有一个集合里至少有两个元素。” 抽屉原理有时也被称为鸽巢原理。

在上述定理中,原理的对象是可重复的(物体),当然,对于不可重复的物体(集合元素)也是满足的。
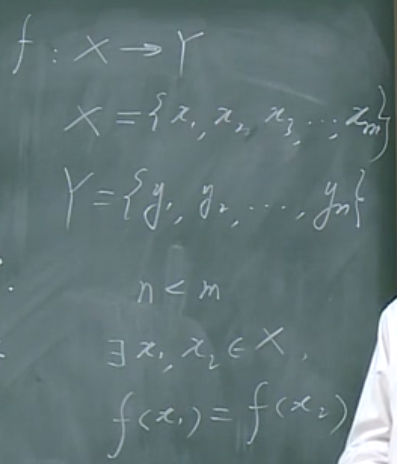
例题

对【例2】的解释:(a_i=2^{s_i}d_i),(s_i)取0或1,(d_i)取1-n间的任一个数字即可。当然,下面的理解也是正确的。
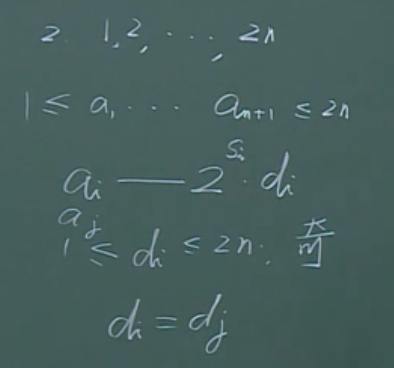
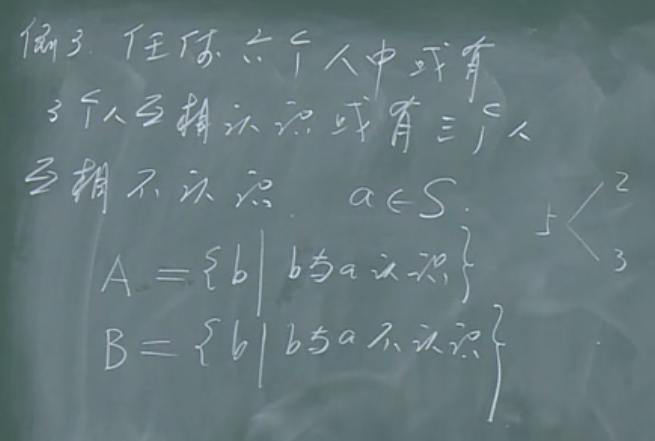
对【例3】的解释:
根据平均性原理,认识a的和不认识a的应该分别分为2、3。(至少有一个集合中,元素个数为3)
-
若(|A|=3),那么,可以进一步将其分为
- 有两个人互相认识。由于他们同时与a认识,即三个人互相认识。那么问题得证。
- 所有人均不互相认识(对于任意的两个人,他们均不互相认识)。那么,问题亦得证。
-
若(|B|=3),那么,可进一步将其分为
- 有两个人互相不认识。由于他们与a也互相不认识,那么,问题得证。
- 所有人均互相认识。问题亦得证。
事实上,如果(|A|=4)、(|A|=5),也可以类似地进行证明。
总之,问题得证。

映射的一般性质
映射的合成
逆映射
定义
存在性
唯一性
左右可逆
引子

置换
定义
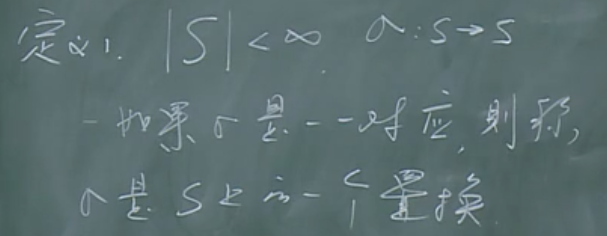
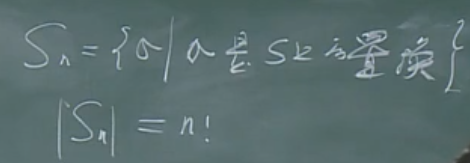
置换的乘积
循环置换
置换的分解
运算
二元运算
运算律
代数系
特征函数
引子
菜谱点菜


定义
【定义1】

集合在计算机中的表示
要求:可方便地放入计算机,且对其处理要有效率。
例子:
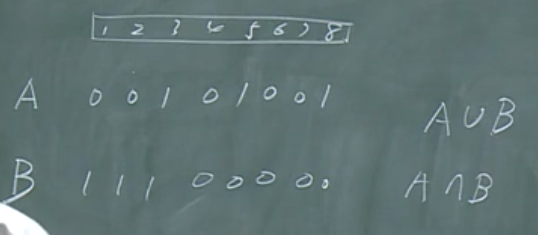
点菜问题的计算机表示,对其的处理为简单的按位操作。
特征函数与集合子集
【定理1】
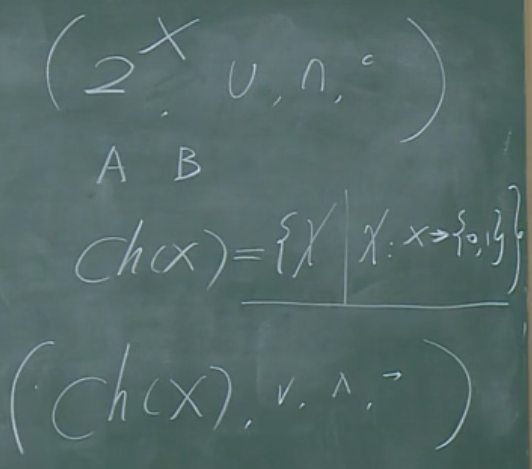
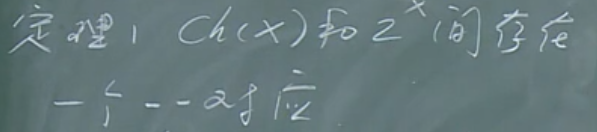
【证明】
构造映射:
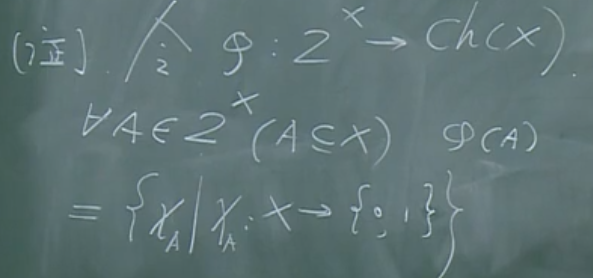
证明其为单射,还为满射:
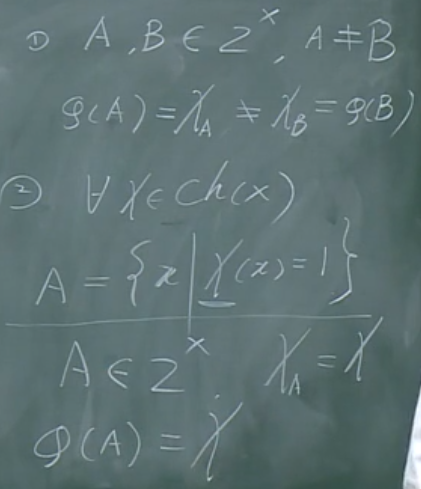
关系
关系的概念
n元关系
二元关系的注意事项
恒等关系、自反关系、反自反的二元关系

恒等关系:

自反关系:集合中每一个元素都成立,比如(le)是自反关系,而(<)不是自反关系。
自反:R的恒等关系在R中。
反自反关系:集合中每一个元素都不成立,比如(<)。
对称关系、反对称关系

对称:R的逆包含在R中。
对称关系:例如,朋友,家人
反对称关系:例如,(xle y),(yle x),则(x=y)显然成立;那么,(le)即为反对称关系。
传递关系

传递:R的平方包含在R中。
关系的逆

关系的运算
关系的集合运算
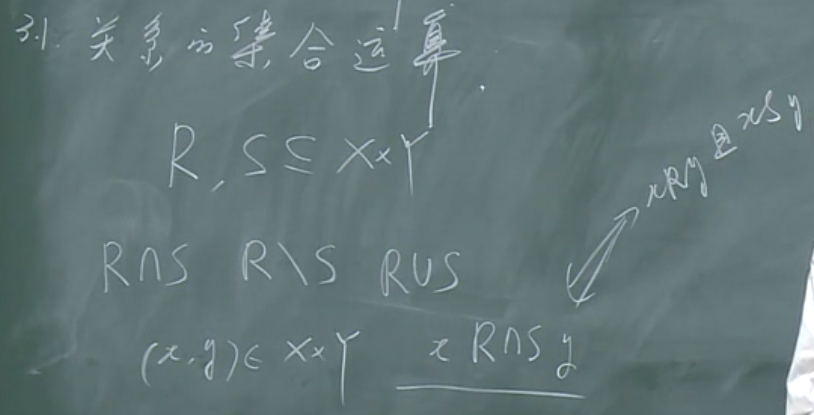
关系的合成运算
定义

性质
结合律:
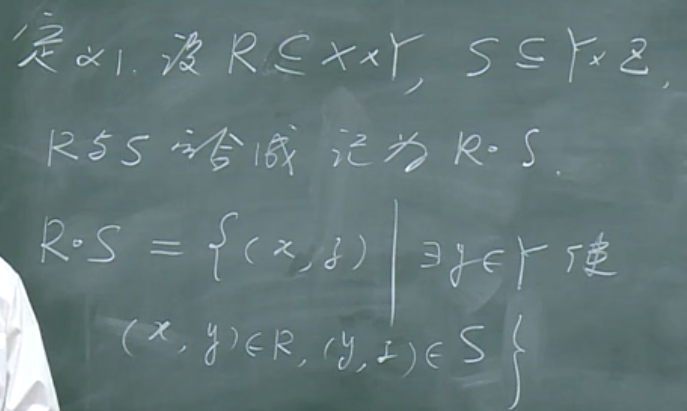
分配律:
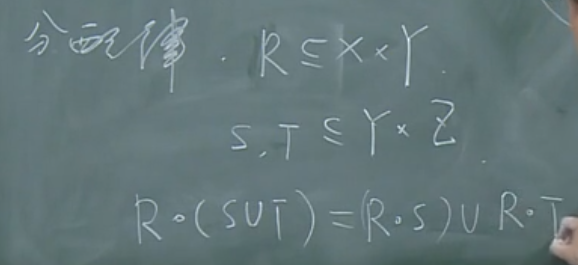
关系的幂运算
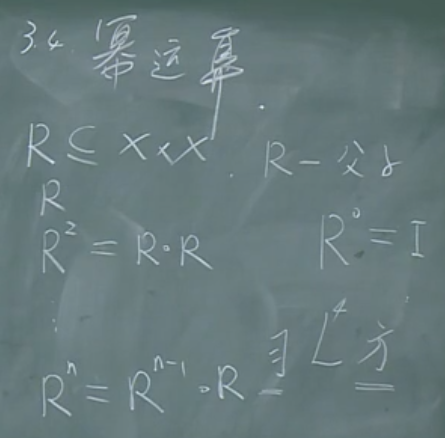
关系的闭包

笛卡尔积的优良性质(自反,对称,传递)在R上不一定具有。
添加最少数量的序偶,使其具有相应的优良性质的一种方法称之为闭包。
传递闭包


证明中最后一句(结论)之前应加上,由(R^+)的任意性。
使逻辑严谨,而不存在跳跃。
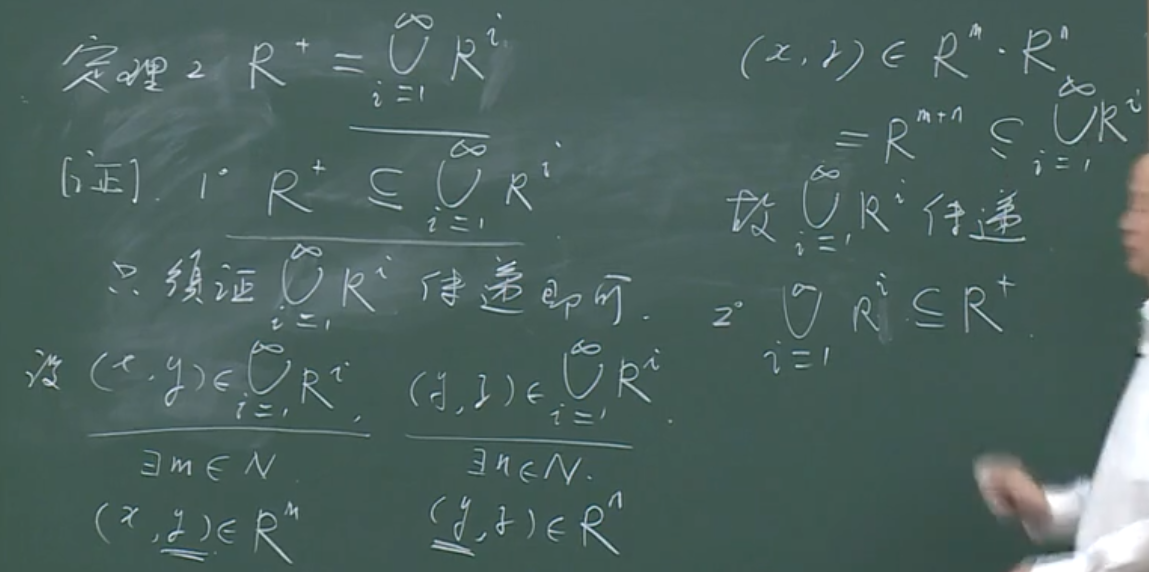
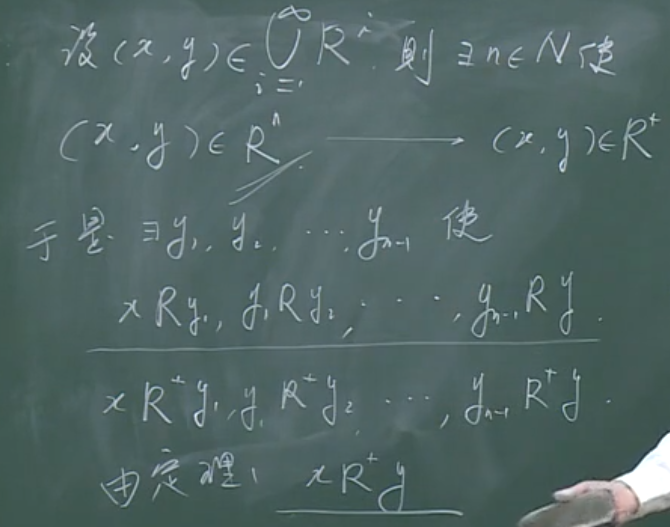
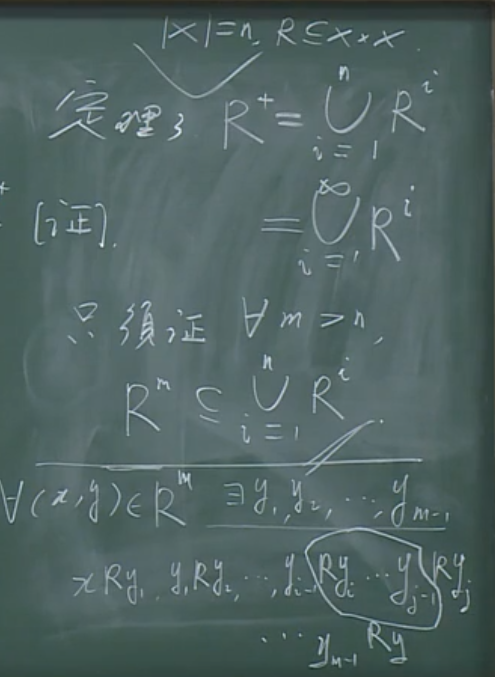
由抽屉原理,做了m次合成,但是元素只有n个。所以y中必然有相等量(集合元素是唯一的,即互异性),假设(y_i=y_j),可以得到圈起来的部分可以省略。
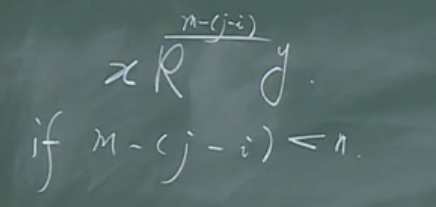
如果(m-(j-i)ge n),重复上述过程,必然得到(p=m'-(j'-i')<n),证毕。
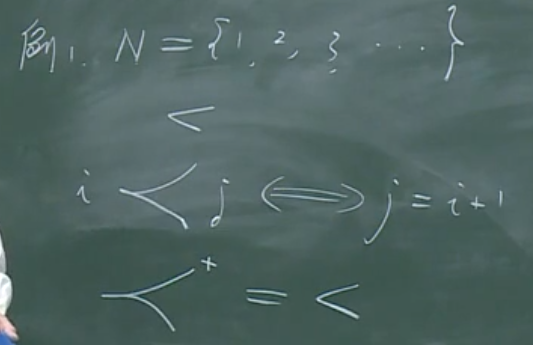
小于关系的由来,先定义关系(iprec jequiv j=i+1),而小于关系就是(prec)的传递闭包,即(prec^+=<)。
本质上说,小于关系是由加法运算定义出来的。先有运算(+),再有关系((prec)),关系上再做传递闭包(甚至是自反传递闭包)可以得到更复杂的关系,最后有代数系统的结构(例如,(N={1,2,cdots})是序结构)。
自反传递闭包
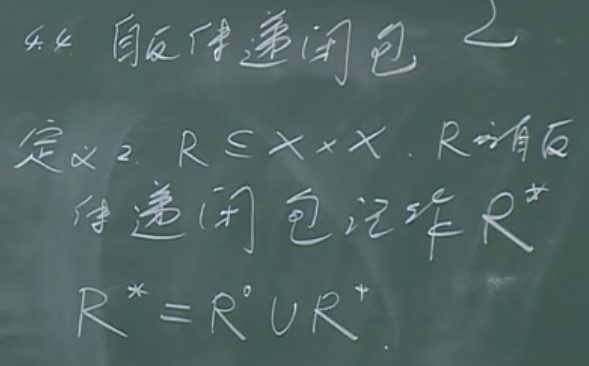
也可以表述为:包含R的所有自反传递关系的交。
【例】文法
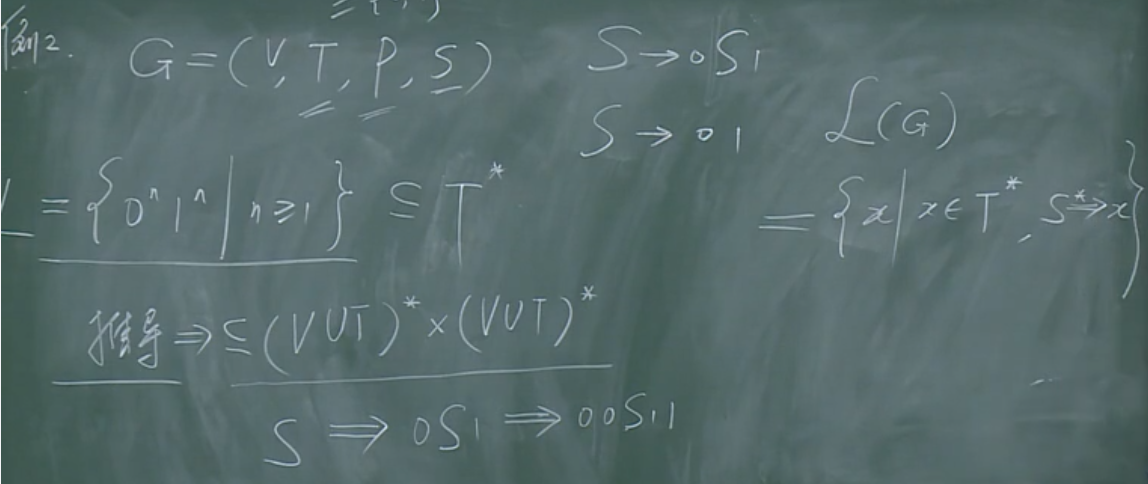
文法的简单例子,(L={0^n1^n|nge 1}subseteq T^*),也就是n个0之后紧跟n个1。
(G=(V,T,P,S)),G是文法,V是非结束字符,T是结束字符,P是规则,S是开始符。
那么,对于这样一个文法,让其动起来的方法是定义其关系:(Rsubseteq (Vcup T)^* imes (Vcup T)^*)。
先有一个开始符号S,S按照P里的规则转换:(S
ightarrow 0S1),(S
ightarrow 01)。
那么,仅有文法的情况下(没有给出(L={0^n1^n|nge 1}subseteq T^*)),怎么描述呢?
关系矩阵
关系运算的布尔矩阵
关系图
等价关系
等价关系
等价关系可以用来对事物进行分类,分类后可以用其中一个来代表。

划分:
在数学中,集合 X 的划分是把 X 分割到覆盖了 X 的全部元素的不交叠的“部分”或“块”或“单元”中。