纹波星(stripe)
【题目描述】
Kirby最近要去Ripple Star拜访Ribbon。但是他觉得空手去不太好,所以他决定带一点小礼物。
Kirby有n种颜色的缎带,每种颜色的缎带有ai条,Kirby希望用上所有的缎带来接成一长条来送给Ribbon。为了美观,长条中相邻的两段的颜色不能相同。驾驶Warp Star到达Ripple Star的路程很漫长,闲得无聊的Kirby想算一算他用这些缎带能接出多少不同的长条呢?作为Warp Star上的计算程序的你需要注意的是,Kirby可能还要在长条的一端接上一些小玩意,所以长条是有左右端之分的。
【输入数据】
第一行一个正整数n。
第二行n个正整数a1~an,表示各颜色缎带的数量。
【输出数据】
输出只有一行,一个整数表示答案。答案对1000000007取模。
【样例输入】
3
1 2 2
【样例输出】
12
【数据范围】
对于20%的数据,n=2;
对于50%的数据,n<=5;
另外20%的数据,ai均相同;
对于100%的数据,1<=n<=15,1<=ai<=5。
【样例解释】
“12323”,“13232”,“21323”,“31232”,“23123”,“23132”,“32123”,“32132”,“23213”,“32312”,“23231”,“32321”,共12种。
题意:给长度为Σai的数列染上n种颜色,每种颜色正好染ai段,相邻段不能染成同色,求方案数。
我们考虑状压,f[i][S][k]表示染了i段,每种颜色剩下的段数状态为S,第i+1段颜色为k的方案数。
显然,f[0][0][x]=1(1<=x<=15)
如何转移?我们枚举第i段染什么颜色(不能与i+1段的重复),f[i][S][i+1段的颜色]+=f[i-1][S'][你当前枚举的颜色]。(这个位置填你当前枚举的颜色)
这样看起来复杂度是n*Σai*ai^n的。但是我们会发现,有一些状态根本不合法,即i必须=Σ剩余的段数。这些状态根本就不会也不能被搜索到。
但是,如果是普通的DP,这些状态很难不被搜索到(至少代码要写很长)。但是记搜可以很好的处理这一点。
我们可以发现i是不用记录的,只要每种颜色剩下的段数都为0,就是DP的边界。
则时间复杂度为n*n*ai^n。
考虑优化。(为了便于说明,i为上面的i)
考虑更改状态的表示,f[k][S]状态S表示每种段数剩下的颜色数有多少种,k表示当前DP做到的最后一段+1(i+1)的颜色的剩余段数。
为了简单起见,我们把状态改成f[k][a1][a2][a3][a4][a5](a1为段数为1的剩下的颜色数有多少种......)
显然,它是可以像上面一样转移的。
我们枚举第i段染的颜色的剩余段数(以剩余段数为3为例)(可以与i+1段的颜色的剩余段数重复)。
(1)与i+1段重复:f[i+1段的颜色的剩余段数][a1][a2][a3][a4][a5]=f[a3-1][a1][a2+1][a3-1][a4][a5]*(a3-1)(即剩余段数为3的其中一种颜色是和i+1段的颜色一致的,扣除,剩余段数为3的其它颜色这个位置都可以填)
(2)不与i+1段重复:f[i+1段的颜色的剩余段数][a1][a2][a3][a4][a5]=f[a3-1][a1][a2+1][a3-1][a4][a5]*a3(即剩余段数为3的颜色这个位置都可以填)
同样的,f[x][0][0][0][0][0]=1。
这样,时间复杂度就降为ai*ai*n^ai。

#include<iostream> #include<cstdio> #include<cstring> using namespace std; long long mod=1000000007ll; long long dp[6][16][16][16][16][16]; int s[6];int n; long long DP(int k,int a[6]) { if(a[0]==n)return dp[k][a[1]][a[2]][a[3]][a[4]][a[5]]=1; if(dp[k][a[1]][a[2]][a[3]][a[4]][a[5]]!=-1)return dp[k][a[1]][a[2]][a[3]][a[4]][a[5]]; dp[k][a[1]][a[2]][a[3]][a[4]][a[5]]=0; for(int i=1;i<=5;i++) { if(a[i]==0||(k==i&&a[i]==1))continue; a[i]--;a[i-1]++;long long y=DP(i-1,a);a[i]++;a[i-1]--; if(k==i)dp[k][a[1]][a[2]][a[3]][a[4]][a[5]]=(dp[k][a[1]][a[2]][a[3]][a[4]][a[5]]+y*(a[i]-1))%mod; else dp[k][a[1]][a[2]][a[3]][a[4]][a[5]]=(dp[k][a[1]][a[2]][a[3]][a[4]][a[5]]+y*a[i])%mod; } return dp[k][a[1]][a[2]][a[3]][a[4]][a[5]]; } int main() { freopen("stripe.in","r",stdin);freopen("stripe.out","w",stdout); memset(dp,-1,sizeof(dp)); scanf("%d",&n); for(int i=1;i<=n;i++) { int b;scanf("%d",&b);s[b]++; } printf("%lld",DP(0,s)); return 0; }
切课本上瘾综合征(textbook)
【题目描述】
众所周知,小Z喜欢切课本,而且是上瘾的那种。
这一天,小G弄来了一本长为N,宽为M的课本请小Z来切。小G想让小Z用P-1刀把课本正好切为P个面积相等的矩形,而且每一刀必须把某一块课本切成两块。小Z自然很高兴,但小G还提出了一个要求,就是要使得这P个矩形中,长和宽比值的最大值最小。这让小Z有些犯难,他希望你能帮帮他,让他痛痛快快地切一次课本。
【输入数据】
输入一行三个正整数N,M,P,表示课本的长、宽和切出的矩形个数。
【输出数据】
输出一行一个浮点数,表示最小的长宽最大比值,当你的输出和标准答案不超过10^-6时,你的答案被视为正确答案。
【样例输入】
5 4 4
【样例输出】
1.250000000
【数据范围】
对于10%的数据,P=2;
对于30%的数据,P<=10;
对于60%的数据,P<=15;
另外10%的数据,M | N且P | (N/M);
对于100%的数据,1<=M<=N<=10000,1<=P<=20。
【样例解释】

先考虑暴力搜索。对于一块长为a,宽为b的矩形,切p刀。
我们把这个矩形分成两个小矩形,其中一个切p1刀,另一个切p2刀。(枚举p1,p2=p-p1)
考虑横着分成两个矩形和竖着分成两个矩形。
竖着切:显然两个小矩形的长之比为p1:p2。

横着切同理:宽之比为p1:p2。
但是这样会TLE。我们会发现,这里面有很多相同状态。
考虑记搜。用f[i][j][k]表示当前对于一个长为j,宽为k的矩形切i刀,长宽比的最小值。
但是j是double,k也是double,怎么存到数组里。
map!把这两个double压成一个int。即变为f[i][S](S为map<j,k>)。
这样就可以记搜了。但是map真是慢,不开O2就T飞了。

#include<iostream> #include<cstdio> #include<map> #include<cstring> using namespace std; typedef pair<double,double> P; map<P,int> mp; double f[21][1000000],tot=0; double Get(double a,double b,int p) { if(a<b)swap(a,b);int now; if(!mp[P(a,b)]){mp[P(a,b)]=++tot;now=tot;} else now=mp[P(a,b)]; if(f[p][now])return f[p][now]; if(p==1)return f[p][now]=a/b; double ans1,ans2,ans=999999999; for(int p1=1;p1+p1<=p;p1++) { int p2=p-p1; ans1=max(Get(a/p*p1,b,p1),Get(a/p*p2,b,p2)); ans2=max(Get(a,b/p*p1,p1),Get(a,b/p*p2,p2)); ans=min(ans,min(ans1,ans2)); } return f[p][now]=ans; } int main() { freopen("textbook.in","r",stdin);freopen("textbook.out","w",stdout); int n,m,p;scanf("%d%d%d",&n,&m,&p); printf("%.15lf",Get((double)n,(double)m,p));cout<<" "<<tot; return 0; }
地衣(lichen)
【题目描述】
小C培养了n组地衣,现在小C要让它们长在一起。他在n组地衣之间划出了m条生长通道,每条生长通道的适宜度分别为wi,两组不同的地衣之间一定会通过其中一条适宜度最高的生长通路长到一起,两组不同的地衣长到一起后,这两组就会合为同一组地衣。同一组地衣之间不会继续生长。小C想知道这n组地衣最终长成一组的时候可以有多少种形态。
【输入数据】
第一行两个正整数n,m,表示地衣组数和通道条数。
接下来m行,每行三个正整数,xi,yi,wi,表示连接第xi组和yi组的生长通道适宜度为wi。
【输出数据】
输出一行一个整数,表示地衣最终长成一组的时候可以有多少种形态,答案对1000000007取模。
【样例输入】
5 5
1 2 1
2 3 1
3 5 2
1 4 2
4 5 2
【样例输出】
2
【数据范围】
对于20%的数据,n,m<=10;
对于40%的数据,n,m<=100;
对于60%的数据,n,m<=10000;
另外20%的数据,同种权值的边不会超过2条。
对于100%的数据,1<=n,m<=100000,1<=xi,yi<=n,1<=wi<=10^9,同种权值的边不会超过8条。
【样例解释】
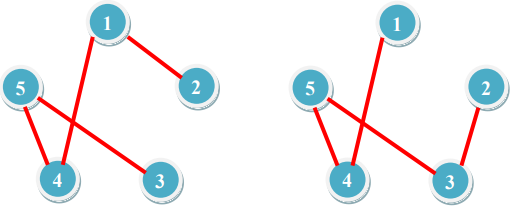
题意:求最大生成树的个数。
一些显而易见的结论:
①最大生成树中的相同权值的边无论在哪一种连接方案中,被选取的边数 和 所连通的点的集合 总是相同的。
这样我们就有了第二条结论
②能对答案产生贡献的一定是相同权值的边,且不同权值的边产生的贡献的是独立的。
这样我们就可以用乘法原理计算答案。
我们开两个并查集,第1个是当前kruskal用到的并查集。第2个用来计算答案。
③对于每一种权值,在两种选取方案中,如果 被选取的边数 相同,那么这两种方案 所连通的点的集合 相同,这两种方案一定都是构成最大生成树的合法方案。
简要说明一下。显然,我们至少要取 被选取的边数 这么多条边,否则不可能是合法方案。且我们的其它方案肯定无法选出>这么多条边,否则最大生成树可以更大。
下图黑圈为做到当前权值前,已选取的连通块
如果Kruskal选取的是黑色的这些边![]()
那么有可能还有一种方案是选取红色的这些边![]()
但是不可能能选取到这条黄色的边
因为如果选这条边,那么Kruskal就也可以选取这条边,使得生成树更大。
所以,只要 被选取的边数 相同,那么 所连通的点的集合 也相同。而只要满足这两个条件,那么由第一个结论可知,这必然也是一个合法方案。
当Kruskal做到某一种权值时,对于这种权值,我们用第一个并查集先求出它用了多少条边(记为x),此时,第二个并查集还停留在原先的第一个并查集的状态。
dfs暴力枚举选取哪些边,但是,这些选取的边不能在同一个集合里,选了一条边后,像Kruskal一样把这条边的两个顶点所在的集合给合并起来。在dfs结束完后,在把这两个顶点给拆开。如果我们成功选取了x条边,那么,这就是一种合法方案。
我们发现,第二个并查集要支持撤销,那么,我们需要按秩合并,即用rank[i]表示i这棵并查集的大小(元素个数),两棵并查集合并,把rank小的作为rank大的并查集的一棵子树(还是找到这两棵并查集的根节点,把rank小的根节点的父亲设为rank大的根节点)。这样,我们撤销时,把我们连的那条边给撤销,就把这两棵并查集给分离了。
然后,这种权值结束后,更新第二个并查集连通的集合(更新到第一个并查集连通的集合)。乘法原理算答案即可。
还有一种情况,这张图根本不连通,这样方案数为0

#include<iostream> #include<cstdio> #include<algorithm> using namespace std; struct xxx{ int u,v,cost; }g[100100]; int fa1[100101],fa2[100101],rank2[100101],n,m; bool cmp(xxx a,xxx b){return a.cost>b.cost;} int find1(int x){return fa1[x]==x?x:fa1[x]=find1(fa1[x]);} int find2(int x){return fa2[x]==x?x:find2(fa2[x]);} void cx2(int x,int y) { if(fa2[x]==y){rank2[y]-=rank2[x];fa2[x]=x;} else {rank2[x]-=rank2[y];fa2[y]=y;} } bool hb1(int x,int y) { int xx=find1(x),yy=find1(y); if(xx==yy)return false;fa1[xx]=yy; return true; } bool hb2(int x,int y) { int xx=find2(x),yy=find2(y); if(xx==yy)return false; if(rank2[xx]<rank2[yy]) {rank2[yy]+=rank2[xx];fa2[xx]=yy;} else {rank2[xx]+=rank2[yy];fa2[yy]=xx;} return true; } void dfs(int T,int N,int k,int x,int &sum) { if(T>N){if(k==x)sum++;return;} int fu=find2(g[T].u),fv=find2(g[T].v); if(hb2(g[T].u,g[T].v)){dfs(T+1,N,k+1,x,sum);cx2(fu,fv);} dfs(T+1,N,k,x,sum); } long long kruskal() { long long ans=1ll; for(int i=1;i<=100000;i++)fa1[i]=i,fa2[i]=i,rank2[i]=1; sort(g+1,g+m+1,cmp); int i=1; while(i<=m) { int I=i,J=i,gs=0,sum=0; for(;g[J].cost==g[I].cost;J++);J--; for(int j=I;j<=J;j++)if(hb1(g[j].u,g[j].v))gs++; dfs(I,J,0,gs,sum);ans=(ans*sum)%1000000007; for(int j=I;j<=J;j++)hb2(g[j].u,g[j].v); i=J+1; } return ans; } int main() { freopen("lichen.in","r",stdin);freopen("lichen.out","w",stdout); scanf("%d%d",&n,&m); for(int i=1;i<=m;i++)scanf("%d%d%d",&g[i].u,&g[i].v,&g[i].cost); long long Ans=kruskal(); for(int i=2;i<=n;i++)if(find1(i)!=find1(i-1)){puts("0");return 0;} printf("%lld",Ans); return 0; }
