1.学习总结
1.1图的思维导图
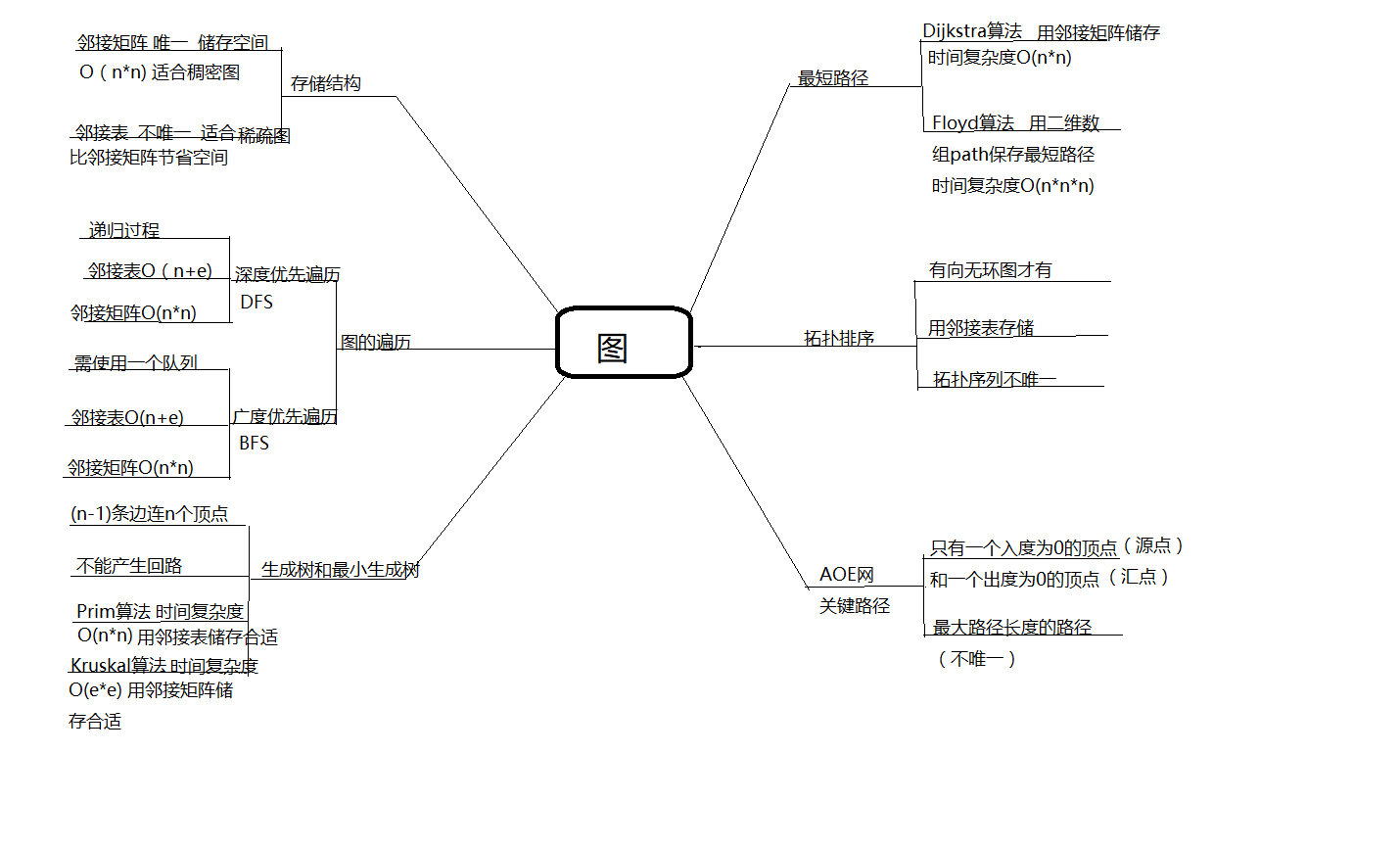
1.2图结构学习体会
深度遍历算法
先访问初始顶点v,再选择一个与v相邻且未被访问过的顶点w为初始顶点,直到所有顶点都被访问完,这实际上是一个递归的过程
广度遍历算法
先访问初始顶点v,再访问所有与v相邻且未被访问的节点,再将其一次作为初始节点依次循环直到访问完所有顶点,这就需要一个队列才能将此算法实现
Prim和Kruscal算法
prim算法是按逐个将顶点连通的方式来构造最小生成树的。
(1)初始状态,TE为空,U={v0},v0∈V;
(2)在所有u∈U,v∈V-U的边(u,v)∈E中找一条代价最小的边(u′,v′)并入TE,同时将v′并入U;
重复执行步骤(2)n-1次,直到U=V为止。
Kruscal算法
<2> 在E中选择一条具有最小权植的边时,若该边的两个顶点落在不同的连通分量上,则将此边加入到T中;否则,即这条边的两个顶点落到同一连通分量 上,则将此边舍去(此后永不选用这条边),重新选择一条权植最小的边。
<3> 如此重复下去,直到所有顶点在同一连通分量上为止。
Dijkstra算法
1)S中存放已找到最短路径的顶点,初始时,集合S中只有一个顶点,即源点V0;
2)T中存放当前还没找到最短路径的顶点;
2、在T集合中选取当前长度最短的一条最短路径(V0,……,Vk),从而将Vk加入到顶点集合S中,并修改源点V0到T中各顶点的最短路径长度;重复这一步骤,直到所有的顶点都加入到集合S中,算法结束。
拓扑排序算法
在DAG图中选择一个没有前驱的顶点 V;从图中删除顶点 V 和所有以该顶点为尾的弧。
2.PTA实验作业
1.题目一:旅游规划
2.设计思路
int main()
{
int 题目中所需的变量
for(int i=0;i<g.n;i++)
for(int j=0;j<g.n;j++)
g.edges[i][j].length=g.edges[i][j].cost=INF;//初始矩阵
for(int i=0;i<g.e;i++)
{
输入数组行列下标
以及所对应标号的路径长度以及收费
}
Dijkstra(g,S,D);//调用狄克斯特拉函数
return 0;
}
3.代码截图


4.提交列表
开始因为编译器选错所以一直编译错误,部分正确是把这道题想成了有向图来做,后来改成无向图的做法就对了
1.题目二:公路村村通
2.设计思路:
void Prim(int v,int n,int e)
{
int lowcost[MAXV];
int min,count=0;
int closest[MAXV];
int k;
for(int i=0;i<n;i++)
{
最低费用存入相应的顶点和边
}
for(int i=1;i<n;i++)
{
min=INF;
for(int j=0;j<n;j++)
if(最低费用不等于0并且小于无穷)
{
将lowcost赋值给min
k=j;
}
总费用等于每次得出的min的和
lowcost[k]=0;
for(int j=0;j<n;j++)
if(每个顶点和边的值不等于0且小于最小费用)
将edges[k][j]赋给lowcost[j]
}
for(int i=0;i<n;i++)
{
if(最低费用不等于0)
{
输出-1
}
}
输出总费用
}
3.代码截图

4.提交列表
忘记定义一个变量来记每条路需最小费用的总和,后来定义了一个count得以解决
输出-1时,少了一个return,加上就好了。但是一直有一个段错误不知道怎么解决。
1.题目三:排座位
2.设计思路
int main()
{
定义宾客1,宾客2,关系
输入数据
if(是朋友)
{
两人可以坐一块
}
else
map[a][b] = map[b][a] = 1;
}
for(int i=0;i<t;i++)
{
int flag1=0,flag2=0;
if(互为朋友)
flag1 = 1;
if(互为死对头)
flag2 = 1;
if(两位宾客之间是朋友且没有敌对关系)
printf("No problem\n");
else if(他们之间有敌对然而也有共同的朋友)
printf("OK but...\n");
else if(他们之间只有敌对关系)
printf("No way\n");
else
printf("OK\n");
}
return 0;
}
3.代码截图

4.提交列表

此题还算好做,开始选错编译器,改过来就好了
3.截图本周题目集的PTA最后排名

4. 阅读代码
#include
using namespace std;
#define MAX 501
#define X 0
#define Y 1
#define VALUE 2
int map[MAX][MAX];
int prevex[MAX];//记录与建立最小生成树可连接的顶点,属于Tree的标记-1
int lowcost[MAX];//记录nearvex[i]的权值
void swap(int &a,int &b)
{
a=a+b;
b=a-b;
a=a-b;
}
int Prim(int v,int e)//顶点数,边数
{
int i, j, sum = 0;
int min = 100;
int a,b;
for( i=1; i<=e; i++)
{
cin >>a >>b;
//if(b < a)swap(a,b);
cin >>map[a][b];
map[b][a] = map[a][b];
}
prevex[0] = 1; //初始顶点为1
prevex[1] = -1;
for( i=1; i
{
//k = search();
for( j=1; j<=v; j++)
{
if(prevex[0] == j)continue;
if(!map[prevex[0]][j])continue;
if(lowcost[j] > 0 && map[prevex[0]][j] > lowcost[j])continue;
if(prevex[j] != -1) //如果顶点j不在MST里
{
if(lowcost[j])
if(lowcost[j] < map[prevex[0]][j])continue;
lowcost[j] = map[prevex[0]][j];
prevex[j] = prevex[0];
}
}
//
min = 100;
int jj = 0;
for( j=1; j<=v; j++)
{
if(!lowcost[j] || prevex[j] == -1)continue;
if(lowcost[j] < min)
{
jj = j;
min = lowcost[j];
}
}
sum += min;
prevex[jj] = -1;
//下一个搜索点
prevex[0] = jj;
}
return sum;
}
int main()
{
int n,v,e;
int i,s=100,sum;
cin>>n;
while(n--)
{
cin >>v >>e;
//memset(memset,0,sizeof(memset));
memset(lowcost,0,sizeof(lowcost));
memset(prevex,0,sizeof(prevex));
sum = Prim(v,e);//构造MST
for(i=1; i<=v; i++)
{
cin>>e;
if(e < s)swap(e,s);
}
cout<< s+sum <<endl;
}
return 0;
}