第486题:
给定一个表示分数的非负整数数组。 玩家 1 从数组任意一端拿取一个分数,随后玩家 2 继续从剩余数组任意一端拿取分数,然后玩家 1 拿,…… 。每次一个玩家只能拿取一个分数,分数被拿取之后不再可取。直到没有剩余分数可取时游戏结束。最终获得分数总和最多的玩家获胜。来源:力扣(LeetCode)
给定一个表示分数的数组,预测玩家1是否会成为赢家。你可以假设每个玩家的玩法都会使他的分数最大化。
1、两个玩家交替选择分数,且两者只能在数组的两边选择分数,也就可以看作是一个递归的过程,当玩家1选择了x,玩家2可以选择除去x后的两边界的两值之一y;
怎么比较玩家1和玩家2能赢呢,可以用当前玩家选择的分数减去对面玩家上次选取赢得自己的分数(这个分数由递归选出),因为有两个选择,我们选择其中那个大的,因为每次选择会使他的分数最大化;
最后判断得到的分数,得出结果。

2、因为递归有许多重复的计算,可以使用动态规划来较少计算;
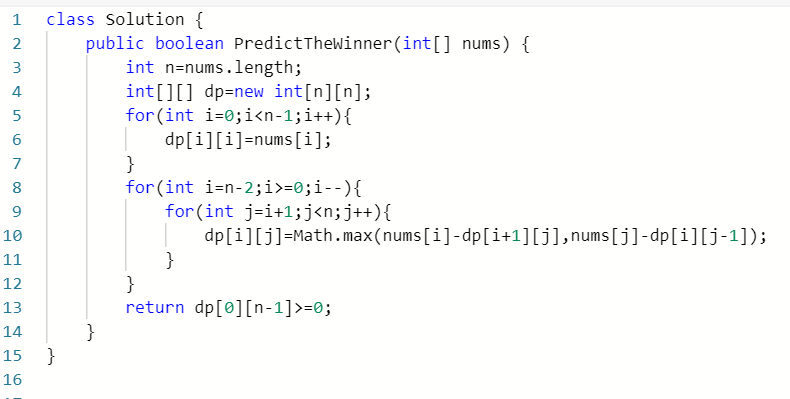
利用二维数组dp[i][j]来存储数组元素,其中横纵长度都为数组长度,i表示数组左边的坐标,j表示右边的坐标,所以只有当 i > j 的时候存在;
当 i = j 时,dp[i][j]=nums[i],当 i < j 的时候,当前玩家可以选择nums[i]或者nums[j],选择这个数后可以使这个玩家的分数最大化;
那么可以得到方程:dp[i][j]=max(nums[i]-dp[i+1][j],nums[j]-dp[i][j-1]),最后来判断dp[0][length-1]内元素即可。