定义
树是一种抽象数据类型(ADT)或是实现这种抽象数据类型的数据结构,用来模拟具有树状结构性质的数据集合。它是由 n(n>0) 个有限节点组成一个具有层次关系的集合。。
二叉搜索树(Binary Search Tree,简称 BST)是一种很常用的的二叉树。它的定义是:一个二叉树中,任意节点的值要大于等于左子树所有节点的值,且要小于等于右边子树的所有节点的值。
如下就是一个符合定义的 BST:
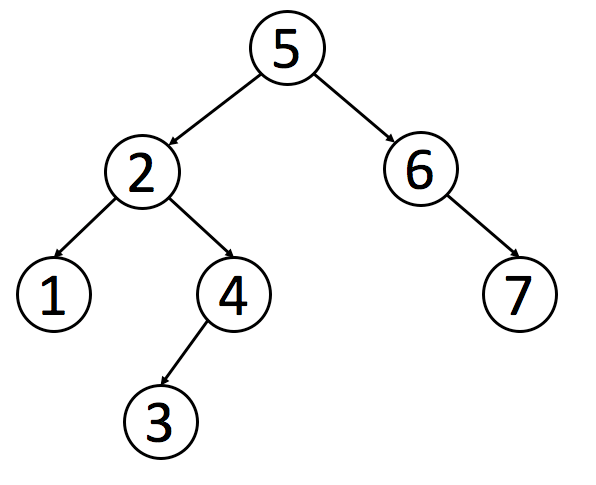
算法模板
void traverse(TreeNode root) {
// root 需要做什么?在这做。
// 其他的不用 root 操心,抛给框架
traverse(root.left);
traverse(root.right);
}
在二叉树框架之上,扩展出一套 BST 遍历框架:
void BST(TreeNode root, int target) {
if (root.val == target)
// 找到目标,做点什么
if (root.val < target)
BST(root.right, target);
if (root.val > target)
BST(root.left, target);
}
前序遍历(递归):
List<int> preorder(TreeNode root) {
List<int> ans = new List<int>();
if (root == null) {
return ans;
}
ans.Add(root.Val);
ans.AddRange(preorder(root.Left));
ans.AddRange(preorder(root.Right));
return ans;
}
中序遍历(递归):
List<int> inorder(TreeNode root) {
List<int> ans = new List<int>();
if (root == null) {
return ans;
}
ans.AddRange(preorder(root.Left));
ans.Add(root.Val);
ans.AddRange(preorder(root.Right));
return ans;
}
后序遍历(递归):
List<int> postorder(TreeNode root) {
List<int> ans = new List<int>();
if (root == null) {
return ans;
}
ans.AddRange(preorder(root.Left));
ans.AddRange(preorder(root.Right));
ans.Add(root.Val);
return ans;
}
前序遍历(迭代/栈):
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> res; //保存结果
stack<TreeNode*> call; //调用栈
if(root!=nullptr) call.push(root); //首先介入root节点
while(!call.empty()){
TreeNode *t = call.top();
call.pop(); //访问过的节点弹出
if(t!=nullptr){
if(t->right) call.push(t->right); //右节点先压栈,最后处理
if(t->left) call.push(t->left);
call.push(t); //当前节点重新压栈(留着以后处理),因为先序遍历所以最后压栈
call.push(nullptr); //在当前节点之前加入一个空节点表示已经访问过了
}else{ //空节点表示之前已经访问过了,现在需要处理除了递归之外的内容
res.push_back(call.top()->val); //call.top()是nullptr之前压栈的一个节点,也就是上面call.push(t)中的那个t
call.pop(); //处理完了,第二次弹出节点(彻底从栈中移除)
}
}
return res;
}
};
中序遍历(迭代/栈):
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> call;
if(root!=nullptr) call.push(root);
while(!call.empty()){
TreeNode *t = call.top();
call.pop();
if(t!=nullptr){
if(t->right) call.push(t->right);
call.push(t); //在左节点之前重新插入该节点,以便在左节点之后处理(访问值)
call.push(nullptr); //nullptr跟随t插入,标识已经访问过,还没有被处理
if(t->left) call.push(t->left);
}else{
res.push_back(call.top()->val);
call.pop();
}
}
return res;
}
};
后序遍历(迭代/栈):
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> call;
if(root!=nullptr) call.push(root);
while(!call.empty()){
TreeNode *t = call.top();
call.pop();
if(t!=nullptr){
call.push(t); //在右节点之前重新插入该节点,以便在最后处理(访问值)
call.push(nullptr); //nullptr跟随t插入,标识已经访问过,还没有被处理
if(t->right) call.push(t->right);
if(t->left) call.push(t->left);
}else{
res.push_back(call.top()->val);
call.pop();
}
}
return res;
}
};
要点
- 二叉树算法设计的总路线:把当前节点要做的事做好,其他的交给递归框架,不用当前节点操心。
- 如果当前节点会对下面的子节点有整体影响,可以通过辅助函数增长参数列表,借助参数传递信息。
- 删除二叉搜索树的节点有三种情况:
- A 恰好是末端节点,两个子节点都为空,那么它可以当场去世了
- A 只有一个非空子节点,那么它要让这个孩子接替自己的位置。
- A 有两个子节点,麻烦了,为了不破坏 BST 的性质,A 必须找到左子树中最大的那个节点,或者右子树中最小的那个节点来接替自己。