一,线性变换
我们用简单的(2 x 2)矩阵说明,对一线性变换M:
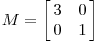
M是对角矩阵,点(x,y)通过线性变换后转化为:
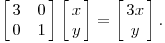
上述变换过程几何上可呈现为:
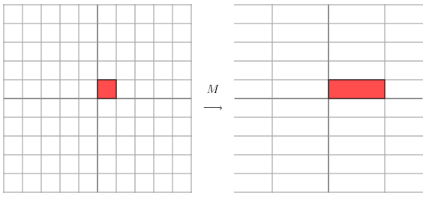
可以看出平面水平方向拉伸为原来的三倍,竖直方向未变。
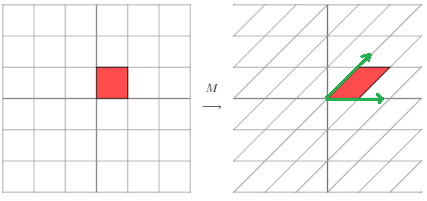
对于另一线性变换M:
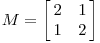
M是对称矩阵,点(x,y)通过线性变换后转化为:
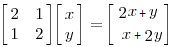

上面这个转换直观上并不容易能看出来,我们可以旋转45度:
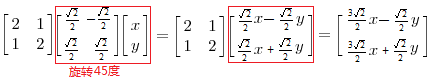

可以看出当旋转坐标后,对应坐标沿某一方向拉伸了三倍。
事实上,对于任意的一个对称矩阵M(非奇异的),线性变换都能像上面一样,先旋转坐标,然后沿某个方向拉伸或收缩坐标。
对一对称矩阵M, 我们求其特征向量和特征值:Mvi = λivi ,从几何学的角度看,vi乘以M, 就相当于对vi作λi 倍的伸缩。(对称矩阵不同特征值的特征向量正交)
上面的例子比较简单,从某一个方向伸缩坐标,下面我们看一下非对称矩阵
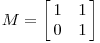
点(x,y)通过线性变换后转化为:
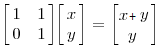
变换后,我们很容易找到一组特征向量来表示向量空间,但此组不相互正交,然后我们仍通过旋转坐标

所以对于一正交基,我们可以通过一般的矩阵(线性变换),转换为另一个正交基。
二,奇异值分解The singular value decomposition
在二维空间中,我们选两个正交的单位向量,v1 和 v2, 如下图,向量Mv1 and Mv2也是正交向量


我们用单位向量u1 和 u2 表示Mv1 和Mv2的方向;其长度用σ1 和 σ2表示,(σ1 和 σ2即为M的奇异值),我们得到:
Mv1 = σ1u1
Mv2 = σ2u2
由于v1 和 v2是单位正交向量,则对于任意向量x可表示为
x = (v1 · x) v1 + (v2 · x) v2 , 其中v· x = vTx,则:
Mx = (v1 · x) Mv1 + (v2 · x) Mv2
Mx = (v1 · x) σ1u1 + (v2 · x) σ2u2
进一步得:
Mx = u1σ1 v1Tx + u2σ2 v2Tx
M = u1σ1 v1T + u2σ2 v2T
用 U 表示列向量u1 和 u2 组成的矩阵,V 表示列向量v1 和 v2组成的矩阵,Σ 表示 σ1 and σ2组成的对角矩阵,
可得:M = UΣVT
This shows how to decompose the matrix M into the product of three matrices: V describes an orthonormal basis in the domain, and U describes an orthonormal basis in the co-domain, and Σ describes how much the vectors in V are stretched to give the vectors in U.(2012-12-31 22:24)
奇异值分解的神奇之处在于可以找到任意矩阵的奇异值分解,How do we do it?
继续用上面的例子说明,我们在domain中标示单位向量的单位圆,经过线性变换Mx后的co-domain中对应的标示图为椭圆,
椭圆的major and minor axes对应于椭圆中最长和最短的两个向量,分别由Mv1 和Mv2定义。
In other words, the function |Mx| on the unit circle has a maximum at v1 and a minimum at v2. This reduces the problem to a rather standard calculus problem in which we wish to optimize a function over the unit circle. It turns out that the critical points of this function occur at the eigenvectors of the matrix MTM.由MTM为对称矩阵,不同特征值对应的特征向量正交,可得到一组正交向量组vi 进而得到对应的奇异值σi = |Mvi| 及向量 ui (Mvi方向上的单位向量)
In practice, this is not the procedure used to find the singular value decomposition of a matrix since it is not particularly efficient or well-behaved numerically.
本文主要来自:http://www.ams.org/samplings/feature-column/fcarc-svd