嗯?这题竟然是个绿题。
这个题真的不(很)难,我们只是不会计算2点之间的距离,他还给出了公式,这个就有点……
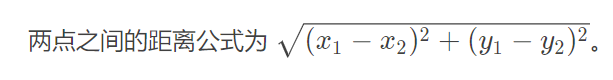
我们直接套公式去求出需要的值,然后普通的状压dp就可以了。
是的状压dp。
这个题的数据加强了,早已经不是搜索可以驾驭的了。
搜索的效率实在是有点低,我来算一个不准的效率,搜索的效率应该是O(n!)。应该是吧。
状压dp只需要短短的O(2^n*n*n就可以了)。状态共有2^n*n个,每次查找下一步需要O(n)的效率,所以状压dp的效率是O(2^n*n*n)。
状压dp用一个二进制数表示哪个奶酪曾经吃过,我们先看看这些二进制数的基本操作:不知道与,或,异或运算的可以百度一下。
第一种操作,查询第i个奶酪有没有吃过。
x表示现在奶酪的情况(2进制数)
我们要判断第i个奶酪有没有被吃
if((x&(1<<i-1))==0)
这样写就可以啦。其中&的意思是按位与运算,就是说在2进制下,2位同时为1,结果才为1,也就是说,如果第i个奶酪被吃掉了,x那一位就是1,按位与运算后的结果也是1,如果按位与运算后的结果是0,第i个奶酪就没有被吃掉。
第二种操作,吃掉第i个奶酪后,x会变成什么样子?
x=x|(1<<i-1)
这样写,|是按位或运算,就是在二进制里,2位有一个为1,结果为1,1<<i-1的第i位是1,和x进行按位或运算就让x的第i位也变成1了。
做这个题只需要这两个操作,剩下的操作有兴趣的同学可以去百度一下。
接下来就是代码了:
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<cstdio>
using namespace std;
double a[20],b[20],shu=999999.0;//初始化
double dp[40000][20];
double sz[20][20];//sz[i][j]是表示第i个奶酪到第j个奶酪有多远。
long long n;
int main()
{
scanf("%lld",&n);
for(int i=0;i<(1<<n);i++)
{
for(int j=1;j<=n;j++)
{
dp[i][j]=999999.0;//还是初始化
}
}
for(int i=1;i<=n;i++)
{
cin>>a[i]>>b[i];
}
a[0]=0;//依然是初始化
b[0]=0;//因为老鼠一开始在0,0的位置。
for(int i=0;i<=n;i++)
{
for(int j=0;j<=n;j++)
{
sz[i][j]=sqrt((a[i]-a[j])*(a[i]-a[j])+(b[i]-b[j])*(b[i]-b[j]));//公式摆着呢,题目给了。
}
}
for(int i=1;i<=n;i++)//1<<i-1是把1左移i-1位,在二进制就是第i位是1。dp[i][j]中的i表示现在的情况(二进制数),j表示现在在哪个奶酪哪里。dp[i][j]的值就是达成这个局势最少走多远。
{
dp[1<<i-1][i]=sz[0][i];
}
for(int i=1;i<=(1<<n)-1;i++)//所有情况,也就是n个1,也就是(1<<n)-1。
{
for(int j=1;j<=n;j++)//在第j个奶酪处。
{
if(dp[i][j]!=999999)//这种情况不可能,比如i=1,j=2;
{
for(int k=1;k<=n;k++)//他的起始点出现过,搜索还能走到哪个奶酪处。
{
if((i&(1<<k-1))==0)//这个奶酪处没来过。
{
dp[i|(1<<k-1)][k]=min(dp[i|(1<<k-1)][k],dp[i][j]+sz[j][k]);//来这个奶酪处。判断一下这样走是不是最近的。
}//有2种可能,第一,之前来过,而且走的距离比这次小,第二种,这次走的距离加上目前位置到第k个奶酪的距离是最短的。反正我们直接找最短的就好。
}
}
}
}
for(int i=1;i<=(1<<n)-1;i++)
{
for(int j=1;j<=n;j++)
{
if(i==(1<<n)-1)
{
shu=min(shu,dp[i][j]);//这里为了方便查找错误写的,可以更优化一点,但没必要。
}
}
}
printf("%.2f",shu);//输出。
return 0;
}
好了,这个题目就这么愉快的讲完了。