
来看题板,这个题大体意思就是,在一个图上,选ABC三个点,然后连接起来,而且在min(AC,BC)+AB的情况下,路径最长是多少?
经过一波缜密的斯烤,我们可以得出一个显而易见的结论“AB一定是树的直径!”(啊一点也不显而易见……当时为合理性纠结了好久……)
啊因为没有任何解释,大家不免会对合理性产生怀疑,然后接下来,我们就用反证法证明一下吧(顺着想真的想不出来,突然想起数学老师说过,如果想证明一个方法是错的,就举一个和他不符的例子)。先假设一个情况,设AB是树的直径,但最长是CE+DE,先假设DE和AB之间有交点,想象图:
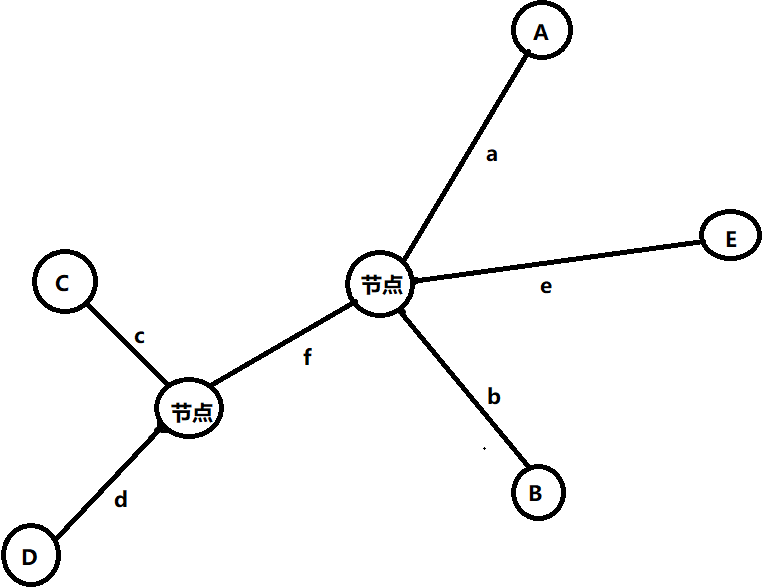
树的直径是一棵树里最长的路径,根据树的直径的定义,我们可以推算出一些公式:
1:a+b>d+f+e
2:b+a>=b+e
3:b+a>=b+d+f
4:a+b>=a+e
5:a+b>=a+d+f
整理一下公式,我们可以得到3个已知事项:
[1]:a+b>d+f+e
[2]:a>=e&&a>=d+f
[3]:b>=e&&b>=d+f
然后,我们假设cd1是三点分别在A,B,C时的最长路径
假设cd2是三点分别在D,E,C时的最长路径。
由上可得:
cd1=a+b+min(c+f+a,c+f+b)=a+b+c+f+min(a,b);
cd2=d+e+f+min(c+d,c+f+e)=c+d+e+f+min(d,f+e);
cd1-cd2=a+b+c+f+min(a,b)-c-d-e-f-min(d,f+e)=(a+b-d-e-f)+f+(c-c)+min(a,b)-min(d,f+e)=(a+b-d-e-f)+(c-c)+min(a,b)-min(d-f,e);
出现分歧了!
现在有两种可能性
1:当d-f<=e时
cd1-cd2就等于(a+b-d-e-f)+min(a,b)-(d-f);
根据上面的[2],我们可以得到a>=d+f>=d-f
根据上面的[3],我们可以得到b>=d+f>=d-f
根据上面的[1],我们可以得到a+b>d-e-f
cd1-cd2最终会变成:一个大于0的数+0+一个大于等于0的数
所以,在d-f<=e的情况下假设不成立。
2:当d-f>e时
cd1-cd2就等于(a+b-d-e-f)+min(a,b)-e;
根据上面的[2],我们可以得到a>=e
根据上面的[3],我们可以得到b>=e
根据上面的[1],我们可以得到a+b>d-e-f
cd1-cd2最终会变成:一个大于0的数+0+一个大于等于0的数
所以,在d-f>e的情况下假设也不成立。
综上所述,假设不成立!
然鹅还有一种情况……
第二种情况,和之前设的一样,只是这次AB和DE不相交
想象图2:
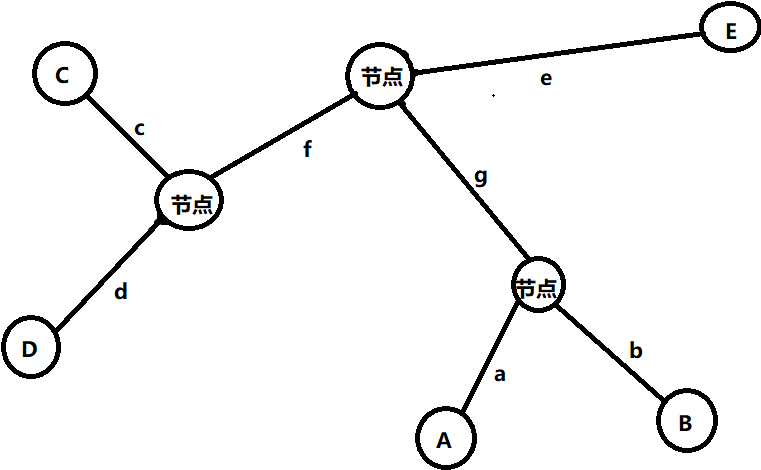
其实和上一个没什么区别(小声bb
由树的直径的性质,我们可以得到一些公式:
1:a+b>d+f+e
2:b+a>=b+e+g
3:b+a>=b+d+f+g
4:a+b>=a+e+g
5:a+b>=a+d+f+g
经过转化:
[1]:a+b>d+f+e
[2]:a>=e+g&&a>=d+f+g
[3]:b>=e+g&&b>=d+f+g
然后,我们假设cd1是三点分别在A,B,C时的最长路径
假设cd2是三点分别在D,E,C时的最长路径。
由上可得:
cd1=a+b+min(c+f+a+g,c+f+b+g)=a+b+c+f+g+min(a,b);
cd2=d+e+f+min(c+d,c+f+e)=c+d+e+f+min(d,f+e);
cd1-cd2=(a+b-d-e-f)+(c-c)+min(a,b)-min(d-f-g,e-g);(具体变换过程请参考第一种假设)
又是分歧!
1:在d-f-g<=e-g的时候
cd1-cd2就等于(a+b-d-e-f)+(c-c)+min(a,b)-(d-f-g);
根据上面的[2],我们可以得到a>=d+f+g>=d-f-g
根据上面的[3],我们可以得到b>=d+f+g>=d-f-g
根据上面的[1],我们可以得到a+b>d-e-f
cd1-cd2最终会变成:一个大于0的数+0+一个大于等于0的数
所以,在d-f-g<=e-g的情况下假设还不成立。
2:在e-g<d-f-g的时候
cd1-cd2就等于(a+b-d-e-f)+(c-c)+min(a,b)-(e-g);
根据上面的[2],我们可以得到a>=e+g>=e-g
根据上面的[3],我们可以得到b>=e+g>=e-g
根据上面的[1],我们可以得到a+b>d-e-f
cd1-cd2最终还是会变成:一个大于0的数+0+一个大于等于0的数
所以,在e-g<d-f-g的情况下假设依然不成立。
综上所属,AB一定是树的直径。
树的直径都会求吧……,不会的话我下一篇博客再写,这一篇实在有点太长了(对我来说
求出树的直径之后,只需要遍历一遍,枚举C点就好了。
好了上代码:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
using namespace std;
long long n,m,a,b,c;
long long head[200005],ans;
long long zc[200005],zd,bh;
long long bhA,bhB,bhAcd[200005],bhBcd[200005];
long long zshu;
struct hehe
{
long long w,cd,syg;
}lsqxx[500005];
void add(long long t,long long w,long long cd)//链式前向星,相信大家都很熟悉
{
ans++;
lsqxx[ans].w=w;
lsqxx[ans].cd=cd;
lsqxx[ans].syg=head[t];
head[t]=ans;
}
void djstl(long long wz,long long bb)
{
for(long long i=head[wz];i!=0;i=lsqxx[i].syg)//迪杰斯特拉求最长路,非常好用
{
if(lsqxx[i].w==bb)
{
continue;
}
if(zc[lsqxx[i].w]<zc[wz]+lsqxx[i].cd)//松弛操作
{
zc[lsqxx[i].w]=zc[wz]+lsqxx[i].cd;
if(zc[lsqxx[i].w]>=zd)//更新最大距离
{
zd=zc[lsqxx[i].w];
bh=lsqxx[i].w;//更新最远距离编号
}
djstl(lsqxx[i].w,wz);//继续查找
}
}
}
int main()
{
scanf("%lld%lld",&n,&m);
for(long long i=0;i<m;i++)
{
scanf("%lld%lld%lld",&a,&b,&c);
add(a,b,c);//双向存图
add(b,a,c);
}
djstl(1,0);//随便选一个点开始遍历
bhA=bh;//bh就是离他最远的一个点,这个点一定是直径的一个端点。存下来
zd=-999999;//初始化
memset(zc,0,sizeof(zc));
djstl(bhA,0);//继续找另一个端点
for(long long i=1;i<=n;i++)
{
bhAcd[i]=zc[i];//记录一下每个点到自己的最远距离
}
bhB=bh;//同上
zd=-999999;
memset(zc,0,sizeof(zc));
djstl(bhB,0);
for(long long i=1;i<=n;i++)
{
bhBcd[i]=zc[i];
}
for(long long i=1;i<=n;i++)//枚举C点
{
zshu=max(zshu,min(bhBcd[i],bhAcd[i]));
}
printf("%lld
",zshu+bhAcd[bhB]);//输出
return 0;
}
啊这可能是我写过的最长的一篇博客了……
结果最后都没讲求树的直径的原理……,啊算了下次再讲吧……