LeetCode 笔记系列12 Trapping Rain Water [复杂的代码是错误的代码]

题目：Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.

　　For example, 
　　Given [0,1,0,2,1,0,1,3,2,1,2,1], return 6.

例如给出上图中的黑色部分（数组表示），让你求出蓝色部分。

这也是个神题。。。当然对小白我来说。

想了半天，是不是遍历数组呢，然后依次计算当前bar构成的container大小。问题在于，这个方法要考虑的边界条件太多了。写了一个很复杂的算法，还用到了stack来记录碎片的蓝色部分，结果最后还是miss很多情况。

后来想了一个复杂度比较高的但是代码看来了比较简单的算法。觉得简直要被BS屎了。但是还是记录下来以村托牛人的牛。

想的方法我取名叫俄罗斯方块法，为啥，你马上就晓得鸟。

把上面的图图，instead of看成一个个柱子，我看成一排排的方块。

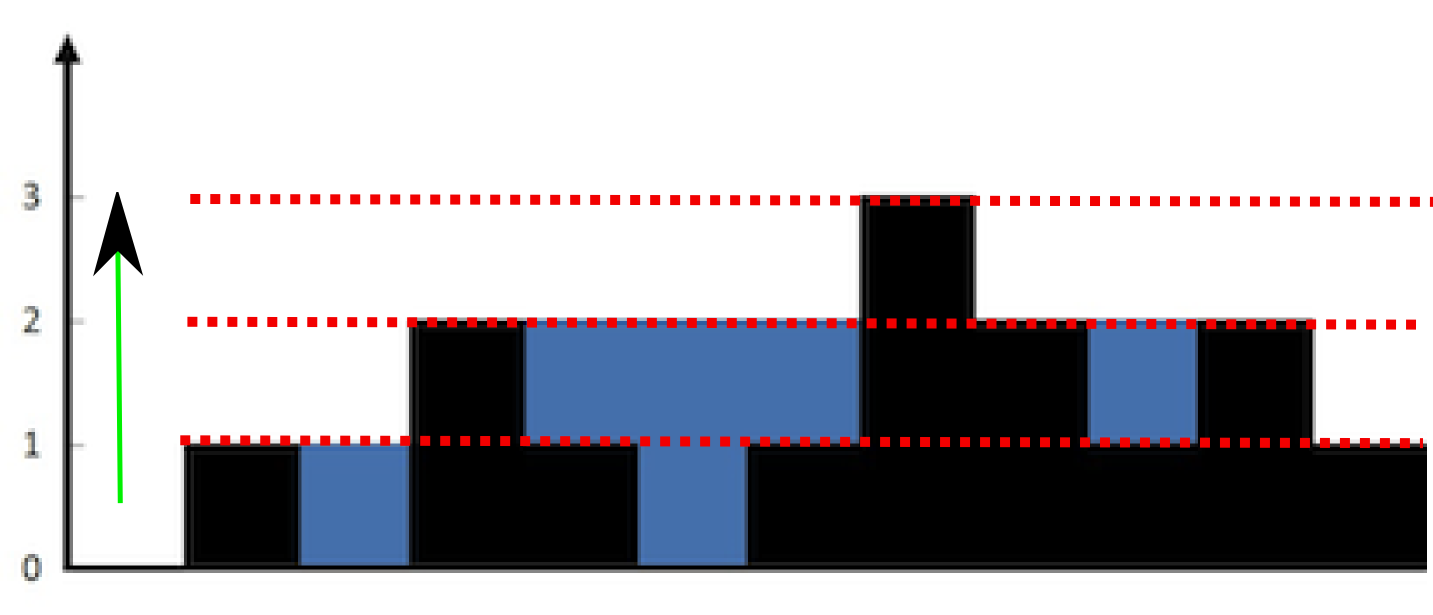
然后，对每一行，我数数有多少蓝色的方块，累加起来，不就是总共的蓝色部分了么。

这个复杂度有点高，取决与最大的元素的值*O(n)。

解法一：

public static int trap(int[] A){
        int i = 0;
        int j = A.length - 1;
        int sumArea = 0;
        while(i + 1 < j){
            //首先找到两边都不是0的位置
            while(A[i] <= 0 && i < j)i++;
            while(A[j] <= 0 && i < j)j--;
            //然后数数当前行有多少蓝色方块，也是就0的个数啦。
            //同时记录最小值
            int min = Integer.MAX_VALUE;
            for(int k = i; k < j;k++){
                if(A[k] == 0) sumArea += 1;
                if(A[k] < min) min = A[k];
            }
            //为记录下一行做准备，消除俄罗斯方块。。。。
            int step = Math.max(min, 1);
            for(int k = i; k <= j; k++){
                if(A[k] > 0)A[k]-= step;
            }
        }
        return sumArea;
    }

然后大集合就可耻地潮湿了。

leetcode的牛人是怎么做的呢？人家不仅有O(n)的解法，而且constant space。膜拜。

首先，找到最高的一个柱子，例如例子中的3。

然后遍历左半边。从i=0开始靠近mid，遍历过程中维护一个curHeight，表示这当前遇到的最大的height值；如果当前的bar的height小于最大值，那么当前的bar能贡献的water就是height - curMaxHeight。否则的话，更新curMaxHeight。

为了更好理解这个算法，我们来track下这个过程：

     

         

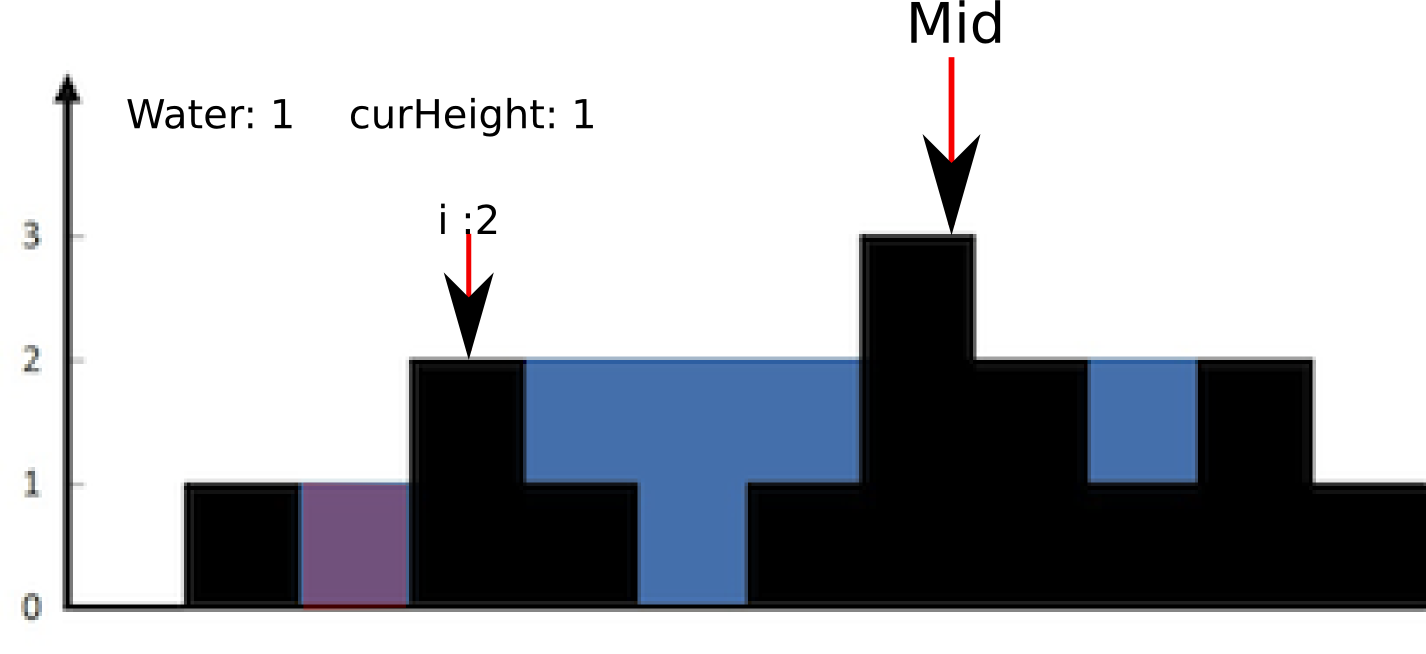
最后遍历右半边。过程是一模一样的，只不过i从最右边靠近Mid。

解法二

代码如下：

public static int trap2(int[] A){
        if(A.length <= 1) return 0;
        int curMaxHeight = 0;
        int water = 0;
        int mid = 0;
        for(int i = 0; i < A.length;i++){
            if(A[i] > A[mid]) mid = i;
        }
        
        for(int i = 0; i < mid; i++){
            if(A[i] < curMaxHeight){
                water += curMaxHeight - A[i];
            }else curMaxHeight = A[i];
        }
        
        curMaxHeight = 0;
        for(int i = A.length - 1; i > mid; i--){
            if(A[i] < curMaxHeight){
                water += curMaxHeight -A[i];
            }else curMaxHeight = A[i];
        }
        return water;
    }

其实，本质上来说，第一步保障了左右两边的水总是能“放进去”，因为大板子在中间档着嘛。

Faint，我写到这里，想到这个代码其实也是蛮简单的，为啥我就没想到呢！唉。。。

总结下：

复杂的代码是错误的代码。没有例外。