kmeans聚类 迭代时间远比层次聚类的要少,处理大数据,kmeans优势极为突出.。
对博客数据进行聚类,实验测试了: 层次聚类的列聚类(单词聚类)几乎要上1小时,而kmeans对列聚类只需要迭代4次!! 快速极多。
如图:包含两个聚类的kmean聚类过程:
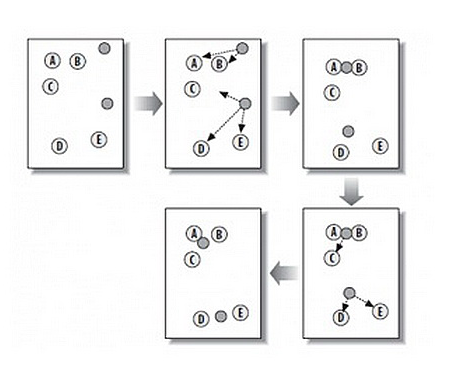
总思路:
将所有要聚类的博客,全部用word表示成一个向量,即每篇博客都是由单词组成的,然后形成了一个单词-博客 的矩阵,矩阵里的权重值就是单词在当前博客出现的总次数。
这样kmeans就是要将这些词频矩阵进行聚类。其实kmeans这里用到的距离相似度是用pearson。
聚类之前,先读取数据文件blogdata.txt.文本如下:

源文件第一列是博客名。第一行从第二列起,是这些博客的单词列表的所有单词。所以这里便有个wordlist。
这里的博客内容全部用单词表示,从第二行开始,每一行都是表示一篇博客。
def readfile(filename): #取得文件的所有内容,用数组存文件的每行数据 lines = [line for line in file(filename)] #获取矩阵的第一行数据,用数组列表columnames存储 所有列名 columnnames = [] columnnames = lines[0].strip().split('\t')[1:] #从数组下标为1的开始取,不要 下标为0的,因为下标为0,是“Blog”,删去,返回的是数组列表 rownames = [] data = [] splitwords = [] datatemp = [] for line in lines[1:]: #从下标为1的line数组里取各行,即从矩阵第二行开始去 splitwords = line.strip().split('\t') #每行的第一列是行名 ,rownames存的是所有行名 rownames.append(splitwords[0]) #剩下部分是该行对应的数据
# data.append(splitwords[1:]) #这里数据虽然是数字,但添加的是string类型,但是应该改成添加float类型 datatemp = [float(x) for x in splitwords[1:]] #即,datatemp存的是所有x的数组:[x]。 等式右边的一开始[]号不能省略啊 data.append(datatemp) # 最终data里的每个元素都是一个datatemp数组,也就是data每个元素就存着 矩阵一行,在本例,data每个元素就是存着一个博客的数据 return rownames,columnnames,rowsdata #rownames是博客名,方便以后将结果树状打印
这里的rownames将是wordnames:

rowsdata就是:
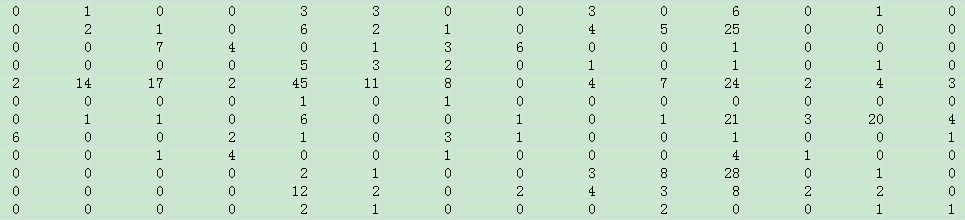
所以kmeans就是对上面这一串数字rowdata进行聚类的。
kmeans聚类步骤:
def kmeanscluster(rowsdata,distance = pearson , finalclusternumberK = 4):
1.随机创建k个中心点(对应博客聚类,则是创k个中心类似博客,但是这k个中心类似博客基本不会命中原来的博客,这k个中心点是新创建的
# 中心值博客的所有列的值(即单词的值)就是最小最大博客的平均值。 例如: 所有行里,对所有列 求出每列的最小大值,然后将两者平均,则中心博客 的所有列就是这些平均值 如:原数据为: 每行表示一个博客,列表示单词。数字表示单词在博客出现的次数。 0 0 2 1 ... 2 3 4 10 ... 4 6 0 0 ... 则对每列进行最小最大值,求出最大最小值博客: 最小值: 0 0 0 0 最大值:4 6 4 10
则中心博客的各列是 最小值博客 和最大值博客的 平均:
2 3 2 5
代码中,rangeslistofAllWords存储则会是:[ (0,4) ,(0,6) ,(0,4),(0,10)...... ] 所以[2,3 , 2, 5....] 就设为中心点
''' 但在下面代码实现中,求中心博客,并不是简单求平均值,而是引用了随机数!!即如radom()*(max-min) + min 若radom()是0.2,则 最终中心博客是; (0.4 0.6 0.4 1 ) + (0 0 0 0) 为: 0.4 0.6 0.4 1 '''
代码如下:
#确定每个点的最小、大值,即确定一个单词 出现次数的最大最小值。即创2行单词数列 的二维数组,定义如下: rangeslistofAllWords=[] for i in range(len(rowsdata[0])): #对所有列进行遍历,每一列的最大最小值找出来,也就是每一个单词的最大最小出现次数找出来 minvalue = min(line[i] for line in rowsdata) maxvalue = max(line[i] for line in rowsdata) Elementofcolumn =(minvalue,maxvalue) rangeslistofAllWords.append(Elementofcolumn) #rangslistofallwords 每个元素里是一个元组
#随机创建k个中心点(对应博客聚类,则是创k个中心类似博客)。 meancluster =[ [(rangeslistofAllWords[j][1] - rangeslistofAllWords[j][0]) * random.random() + rangeslistofAllWords[j][0] for j in range(len(rowsdata[0]))] for i in range(0,finalclusternumberK)] # 创建i行 j列二维数组,i*j
2. 遍历数据所有行(即遍历所有博客),为每行找到匹配的中心点。 计算每行与每个中心点的距离(这里用的pearson距离),
对每行,匹配中心点,找出与该行距离最小的中心点,从而归入到该中心点的簇去,即放进lowestDistanceMatches[]去。记住放进去的是ID,而不是这些行本身。这样会简洁很多
#设置匹配列表 (如果用字典表示,怎样实现呢???? lowestDistanceMatches =[[]for i in range (finalclusternumberK)] #初始化:二维数组,列表套列表 = ,并定义它列表的长度 #遍历数据的所有行,为每行找到匹配的中心点 (即距离该行最小的中心点) for j in range(len(rowsdata)): #遍历所有行 row = rowsdata[j] #方便记住row该行对应的id :j IndexofBestMatchmeancluster = 0 lowestdistance = distance(row,meancluster[0]) #初始化最小距离 for i in range(finalclusternumberK): #遍历所有的中心点 if distance(row,meancluster[i])< lowestdistance: lowestdistance = distance(row,meancluster[i]) IndexofBestMatchmeancluster = i # 只传下标ID, 跟选择排序一样。 lowestDistanceMatches[IndexofBestMatchmeancluster].append(j) # j是该行的下标,IndexofBestMatchmeancluster 为该行匹配的中心点的下标
3.把中心点变成其所有成员的平均位置处
#中心点重新分布,中心点为所在簇的平均值 for i in range(finalclusternumberK): #遍历所有的中心点 newmeanrowforallWords = [0.0]*len(rowsdata[0])#很重要!! 初始化了数组列表,并且定义 数组列表的长度 ,为什么不[for i range(len(rowsdata))]呢?? #遍历同一个簇下的所有行,从而求得 平均值的行 if len(lowestDistanceMatches[i] )>0: #有一些中心点是聚不到元素 for rowid in lowestDistanceMatches[i]: #lowestDistanceMatches[i] 存储着那些 聚敛在一起的博客行 。相当与二维数组[i][rowid] # print 'one ' for colid in range(len(rowsdata[0])): # 遍历中心点的所有列 newmeanrowforallWords[colid]+= rowsdata[rowid][colid] for j in range(len(newmeanrowforallWords)): #求平均 newmeanrowforallWords[j]/=len(lowestDistanceMatches[i]) # print newmeanrowforallWords meancluster[i]=newmeanrowforallWords
4. 迭代第2,3步,直到 lowestDistanceMatches[]里的元素不再变化。(要比较是否变化,就要多设一个以前匹配列表lastmatches来比较)
lastmatches = None for times in range(100): print '迭代 第%d 次:' % times
#在这里插入第2,3 步的 代码。第2,3步代码都与上一句print对齐,同属for times的内容。 最好是将下面终止条件一段代码,放在第2,3步代码 之间,可以早点break迭代
#终止条件: lowestDistanceMatches 匹配结果没变过,则说明聚类完成,结束 if lowestDistanceMatches == lastmatches: break lastmatches = lowestDistanceMatches
最终的目的就是求出lowestDistancematches[]
return lowestDistanceMatches
到此,kmean函数定义完成。
定义pearson距离 函数:
def pearson(v1,v2): # Simple sums sum1=sum(v1) sum2=sum(v2) # Sums of the squares sum1Sq=sum([pow(v,2) for v in v1]) sum2Sq=sum([pow(v,2) for v in v2]) # Sum of the products pSum=sum([v1[i]*v2[i] for i in range(len(v1))]) # Calculate r (Pearson score) num=pSum-(sum1*sum2/len(v1)) den=sqrt((sum1Sq-pow(sum1,2)/len(v1))*(sum2Sq-pow(sum2,2)/len(v1))) if den==0: return 0 return 1.0-num/den
对列聚类,定义转置矩阵 rotatematrix 即可。
最后,运行kmeans函数:
blognames ,wordnames, rowsdata = HierarchicalCluster.readfile("blogdata.txt") choice = int (raw_input(' 请输入:1表示行聚类:博客聚类; 输入2表示列聚类,单词kmeans聚类: ')) if choice == 1 : #为什么加了一个if ,运行就有问题??? print '行聚类:博客聚类 开始:' clusters = kmeanscluster(rowsdata, finalclusternumberK=4) #遍历结果,输出结果 for i in range(len(clusters)): print [ blognames[j] for j in clusters[i]] #一句输出等于下面三句! # for j in clusters[i]: # print '%s ,'% blognames[j], # print '\n' else: print '列聚类(单词kmeans聚类)如下:' colsdata = rotatematrix(rowsdata) clusters = kmeanscluster(colsdata, finalclusternumberK=10) #遍历结果,输出结果 for i in range(len(clusters)): print [ wordnames[j] for j in clusters[i]] #一句输出等于下面三句!
运行结果:

缺点:
结果并不能如层次聚类那样图形化展示出来,还没找到这样第三方库,
树状图展示结果,效果会更好
附层次聚类代码:
def hcluster(rowsdata , distance = pearson): '''层次聚类:所有原始数据项当做一组聚类,最终所有组至底向上地聚类成一个聚类。 这里对 矩阵行 (行表示博客) 进行聚类,每一行数据当成一组。即对博客进行聚类,相似的博客聚在一起 循环体遍历计算: 每一组可能的配对 并计算它们的相关度closest,以此找到最佳配对。 相关度 用pearson距离来衡量 最佳匹配的两个聚类合并成一个聚类, 新生成的聚类所包含数据 等于 两个旧聚类的数据 求均值 的结果 一直循环直到只剩下一个聚类cluster[0]为止 变量定义: distances是一个字典,存储所有距离的计算值 id =i 表示第i个博客, lowestDistacePair =(i,j)表示一个元组,当前最小距离的一对,这一对簇即将合并成一个簇。 rowsdata[i]和vec存的内容都是:[0.0, 1.0, 0.0, 3.0, ''' currentclustid = -1 distancesDic = {} #distances是一个字典,存储所有距离的计算值 。如果是行聚类,存储距离的字典不会很大,因为是博客作为key.而如果是列聚类,字典会很大,因为单词word作为key.所以列聚类就不存储 这些距离了。直接比较 。 #最开始的聚类是数据集的行 '''所有聚类都放在一个数组cluster里,数组rowsdata会传到bicluster类的vec参数去。 clust是一个列表数组,该数组每个元素就是存着rowsdata一个元素,而rowsdata存的是矩阵一行的元素, 总之,clust数组存的是博客数组,一个元素存的是一个博客。clust数组一个元素就是矩阵一行 ''' clust = [bicluster(rowsdata[i],id = i) for i in range(len(rowsdata))] '''id =i 这一步很重要 ,第几个博客,则id为几。 等于第i行数据 clust存的是矩阵的每行。rowsdata每个元素赋给vec。 rowsdata[i]和vec存的内容都是:[0.0, 1.0, 0.0, 3.0,''' while len(clust)>1: #当聚类还剩最后一个,则跳出循环 lowestDistacePair = (0,1) closestness = distance(clust[0].vec , clust[1].vec) #先对矩阵第一行和第二行聚类,即对第一个博客、第二个博客聚类. #遍历每一个配对,寻找最小距离的一对,即找 lowestDistancePair for i in range(len(clust)): #一个clust[i]就代表一个博客 for j in range(i+1,len(clust)): #range(i,)添加 i很重要,这样就不用重复计算以计算好的距离,因为计算<i,j>距离和<j,i>距离是一样的,所以添加一个范围(i,)就省下极多时间 '''上面的字典distancesDic 那五句代码,可以不用,只用下面一句代码代替即可,只用下面 一句代码意思是,不需要存储距离''' d = distance(clust[i].vec ,clust[j].vec) if d<closestness : closestness = d lowestDistacePair = (i,j) #计算两个聚类的平均值 (在找到了最小距离的一对lowerstDistancePair后),作为新合并簇的博客值 vec mergevec = [] #mergevec是数组 mergevec = [ (clust[lowestDistacePair[0]].vec[i] + clust[lowestDistacePair[1]].vec[i]) /2.0 for i in range(len(clust[0].vec)) ] #vec内容是:[0.0, 1.0, 0.0, 3.0,.....所以vec也是一个数组 #建立新的聚类簇,更新该簇信息 newcluster = bicluster( mergevec,left = clust[lowestDistacePair[0]], right = clust[lowestDistacePair[1]], distance = closestness, id = currentclustid ) #新合并的簇的id都是负数,currentclustid都是负数 #不在原始集合中的聚类(即新合并的聚类),其id为负数。 currentclustid -=1 #删去在clust的已经被合并的最小聚类。每次都删去最小的一对,以找下一对。。 #del数组是先要del[1],再del[0].顺序不能反。 #不然出错IndexError: list assignment index out of range:引用超过list最大索引。删除一定要先删除下标最大的,再删除下标最小的??是吗? del clust[lowestDistacePair[1]] del clust[lowestDistacePair[0]] clust.append(newcluster) #最终是将clust数组里所有元素都删掉,直到clust元素还剩下一个,即clust[0]. return clust[0]