学习笔记_深度学习的数学基础

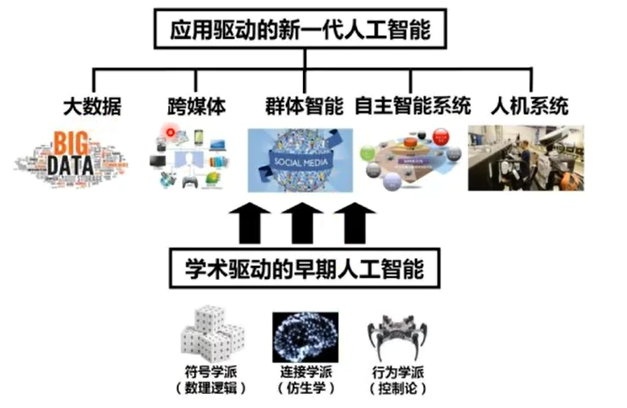
一、数学基础

Al数理基础：线性代数、概率统计、最优化、（信息论、微积分）

　　1.神经网络在“学”什么

 

　　2.矩阵线性变换

 

从线性变换的角度，矩阵相乘对原始向量同时施加方向变化和尺度变化

对于有些特殊的向量，矩阵的作用只有尺度的变化而没有方向变化

->这类特殊的向量就是特征向量，尺度变化系数就是特诊值

　　3.线性代数：秩

矩阵秩的定义

线性方程组的角度：度量矩阵行列之间的相关性

->如果矩阵的各行或列是线性无关的，矩阵就是满秩的，也就是秩等于行数

 

数据点分布的角度：表示数据需要的最小的基的数量

->数据分布模式越容易被捕捉，即需要的基越少，秩就越小

->数据冗余度越大，需要的基就越少，秩越小

->若矩阵表达的是结构化信息，如图像、用户-物品表等，各行之间存在一定相关性，一般是低秩的

　　4.机器学习：数据降维

较大奇异值包含了矩阵的主要信息

只保留前r个较大奇异值及其对应的特征向量（一般r取d/10就可以保留足够信息），可实现数据从n x d降维到（n x r + r x r + r x d）

　　5.低秩近似

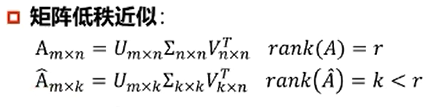
低秩近似的意义：
保留决定数据分布的最主要的模式/方向（丢弃的可能是噪声或其它不关键信息）

应用：

图像去噪

1. 数据矩阵X一般同时包含结构信息和噪声
2. 矩阵分解为两个矩阵相加，一个是低秩的（结构信息造成行或列间线性相关），另一个是稀疏的（噪声是稀疏的）

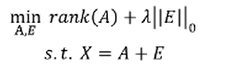
1. 机器学习中的数学基础

概率是基础

支持向量机涉及很多数学基础

梯度下降是神经网络共同的基础

 

二、机器学习三要素：模型、策略、算法

模型：对要学习问题映射的假设（问题建模，确定假设空间）

策略：从假设空间中学习/选择最优模型的准则（确定目标函数）

算法：根据目标函数求解最优模型的具体计算方法（求解模型参数）

 

1. 概率/函数形式的统一

 

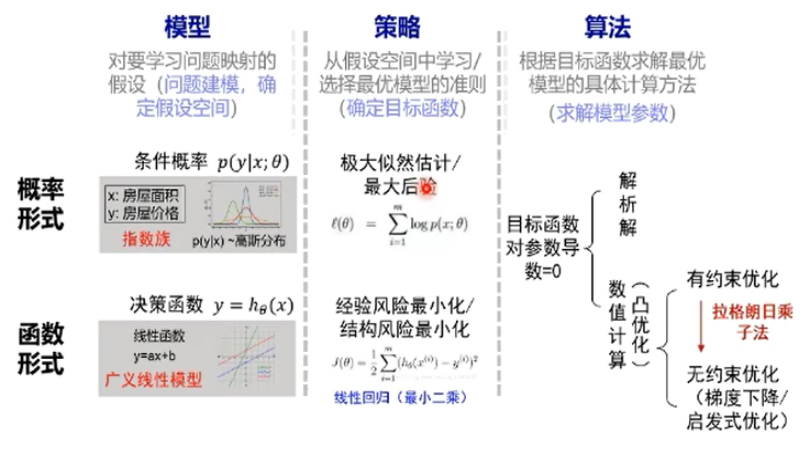
指数族：对常见分布的简化模式

广义线性模型和指数族有一对一的关系

例子：

 

部分问题：

1. 逐层训练时，在训练下一层，上一层的参数冻结吗？

要冻结

　　2.逐层预训练初始化参数有什么依据不？为什么这样就不会出现或者很难出现局部极小值啊？

利用数学方法使其收敛，最后希望落到比较好的局部极小值

　　3.统计机器学习方法与符号主义和连接主义是怎样的关系？是否是连接主义已可以取代统计的方法？

不是 决策树更多是符号主义

都要学

　　4.知识作为先验结合深度学习，这里的知识怎么一般化？

关键是知识的表示，可以利用图神经网络进行知识的表示。

　　5.知识图谱和深度学习在计算机视觉的应用案例有哪些？

区分物体

1. 策略设计：训练误差->泛化误差

“最合适”的模型：机器学习从有限的观测数据中学习出规律，并将总结的规律推广应用到未观测样本上 ->追求泛化性能

 

 

 

 

->衡量训练误差与泛化误差的差异：
计算学习理论（处于研究状态）

PAC给出了实际训练学习器的目标：
从合理数量的训练数据中通过合理计算量学习到可靠的知识

1. 合理数量训练数据：数据集大小
2. 合理计算量：学习训练的时间
3. 可靠的知识：概率的置信度，近似的误差上界

 

1. 策略设计：无免费午餐定理

当考虑在所有问题的平均性能时，任意两个模型都是相同的

 

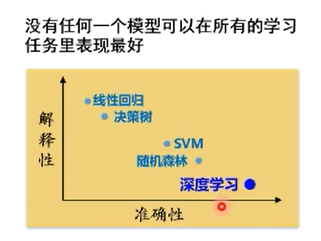
->脱离具体问题，谈‘什么学习算法更好’毫无意义

 

1. 策略设计：奥卡姆剃刀原理

“如无必要，勿增实体”即“简单有效原理”

思考：深度学习是否违背奥卡姆剃刀原理？（参数个数>训练样本数）

答案是开放

我认为并不违背，深度学习比很多传统更好。深度学习复杂度评估正在讨论。

如果多个模型能够同等程度地符合一个问题的观测结果，应该选择其中使用假设最少的->最简单的模型

 

 

 

 

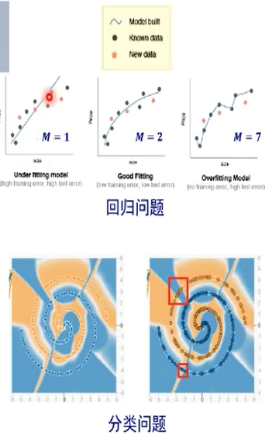
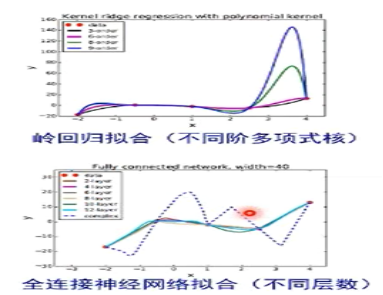
上述现象还在解释中。神经网络有减小过拟合产生的机制。

欠拟合：提高模型复杂度

1. 决策树：拓展分支
2. 神经网络：增加训练轮数

过拟合：降低模型复杂度

1. 优化目标加正则项
2. 决策树：剪枝
3. 神经网络：early stop、dropout

数据增广（训练集越大，越不容易过拟合）

计算机视觉：图像旋转、缩放、剪切

自然语言处理：同义词替换

语音识别：添加随机噪声

　　6.损失函数

 

 

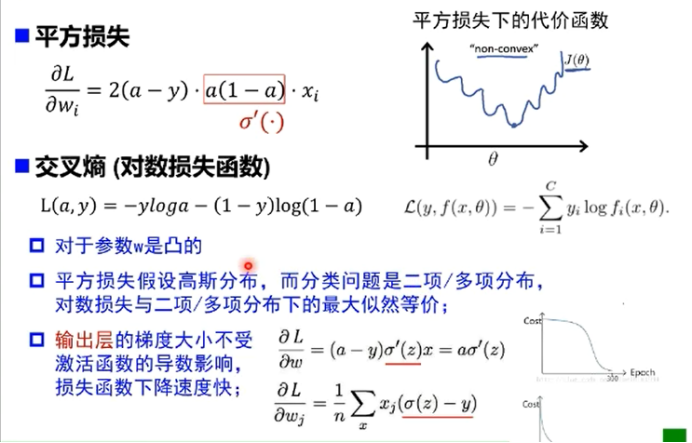
只是在输出层没有问题，在前面依然有问题

三、频率学派 vs 贝叶斯学派

概率论代表了一种看待世界的方式：

对随机事件发生的可能性进行规范化数学描述

对可能性的不同解读促生了概率论的两个两个学派：频率学派/贝叶斯学派

频率学派：

关注可独立重复的随机试验中单个事件发生的频率

可能性：事件发生频率的极限值->重复试验次数趋近于无穷大时，事件发生的频率会收敛到真实的概率

->假设概率是客观存在且固定的

->模型参数是唯一的，需要从有限的观测数据中估计参数值

 

贝叶斯学派：

关注随机事件的“可信程度”，如天气预报明天下雨的概率（无法重复）

->可能性 = 假设 + 数据 ：数据的作用是对初始假设作出修正，使观察者对概率的主观认识（先验）更接近客观实际（观测）

->模型参数本身是随机变量，需要估计参数的整个概率分布

 

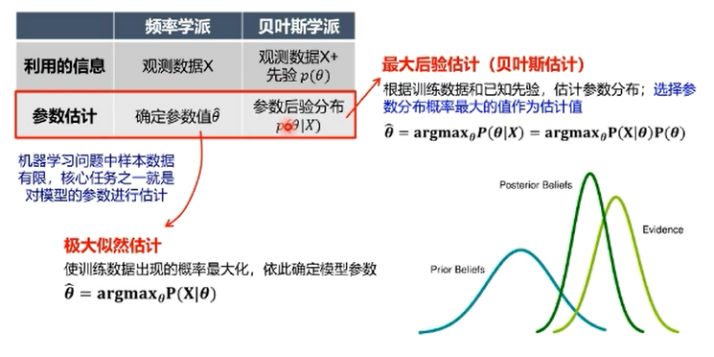
频率学派vs机器学习方法

 

补充：Beyond深度学习

因果推断

统计机器学习：寻找相关性

X -------------------------> Y

相关性不可靠：Yule-Simpson悖论

相关关系可能由于新变量的增加而改变  利用相关性得到结果不一定是准确的

因果性 = 相关性 + 忽略因素

利用因果特征进行判断

联结主义 vs 贝叶斯：相关性 vs 因果性

因果网络：基于贝叶斯网络增加因果限制-父节点必须是子节点的原因

 

群体智能