LeetCode第 190 场周赛

 直接模拟就好了

class Solution {
public:
    int isPrefixOfWord(string sentence, string searchWord) {
        int ans = 1;
        for(int j = 0; j < searchWord.size(); ++j) {
                    
            if(sentence[j] != searchWord[j]) {
                break;
            }
            cout << j << endl;
            if(j == searchWord.size() - 1) {
                return ans;
            }
        }    
        for(int i = 0; i < sentence.size(); i++) {
            if(sentence[i] == ' ') {
                ans++;
                for(int j = 0; j < searchWord.size(); ++j) {
                    
                    if(sentence[i + j + 1] != searchWord[j]) {
                        break;
                    }
                    cout << j << endl;
                    if(j == searchWord.size() - 1) {
                        return ans;
                    }
                }    
            }

        }
        return -1;
    }
};

 

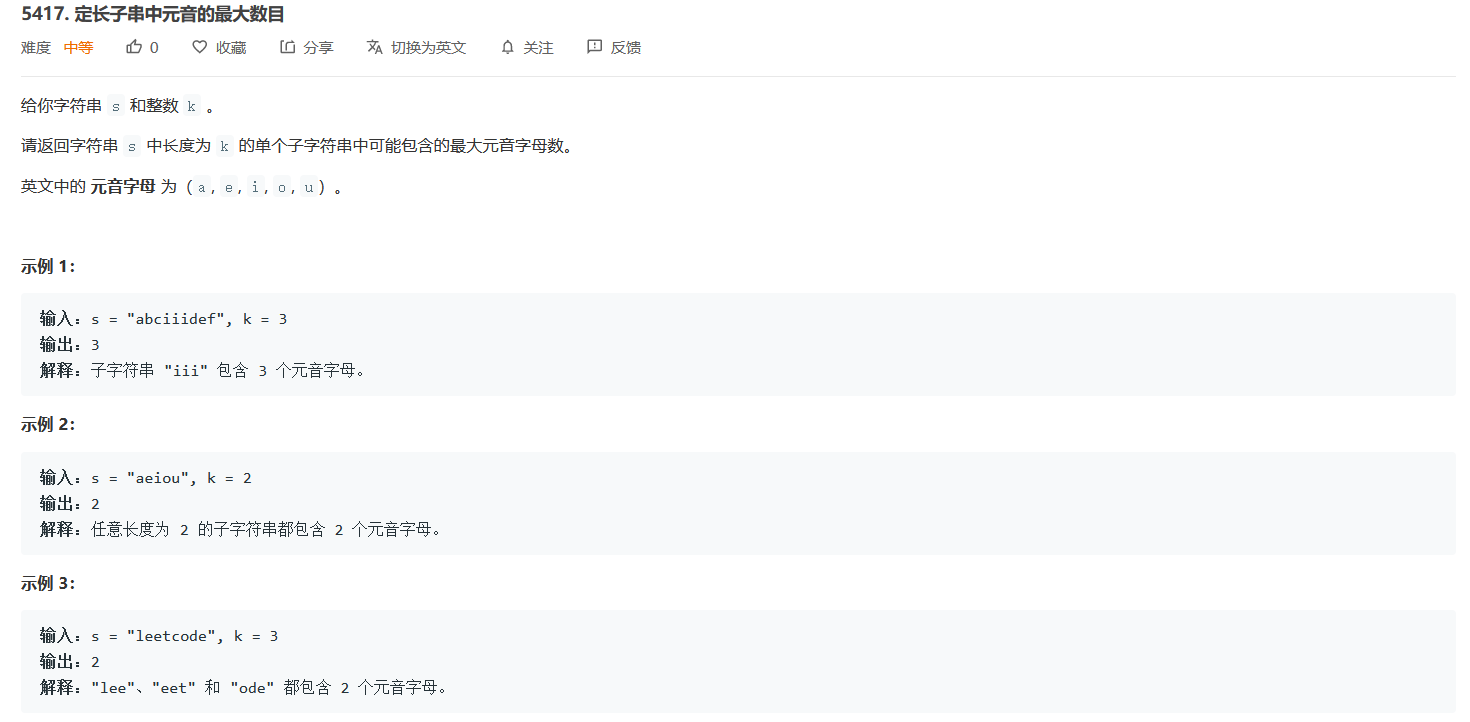
 利用前缀和求解（SB题 数据规模不只有1e5 题目要求出现问题==一直wa）

class Solution {
public:
    
    int maxVowels(string s, int k) {
        for(int i = 0; i < 100005; ++i) {
            a[i] = 0;
        }
        for(int i = 0; i < s.size(); ++i) {
            if(s[i] == 'a' || s[i] == 'e' || s[i] == 'i' || s[i] == 'o' || s[i] == 'u') {
                a[i + 1]++;
            }
            a[i + 1] += a[i];
        }
        int ans = 0;
        
        for(int i = 0; i <= s.size(); i ++) {
            ans = max(ans, a[i + k] - a[i]);
        }
        return ans;
    }
private:
    int a[1000050];
};

 

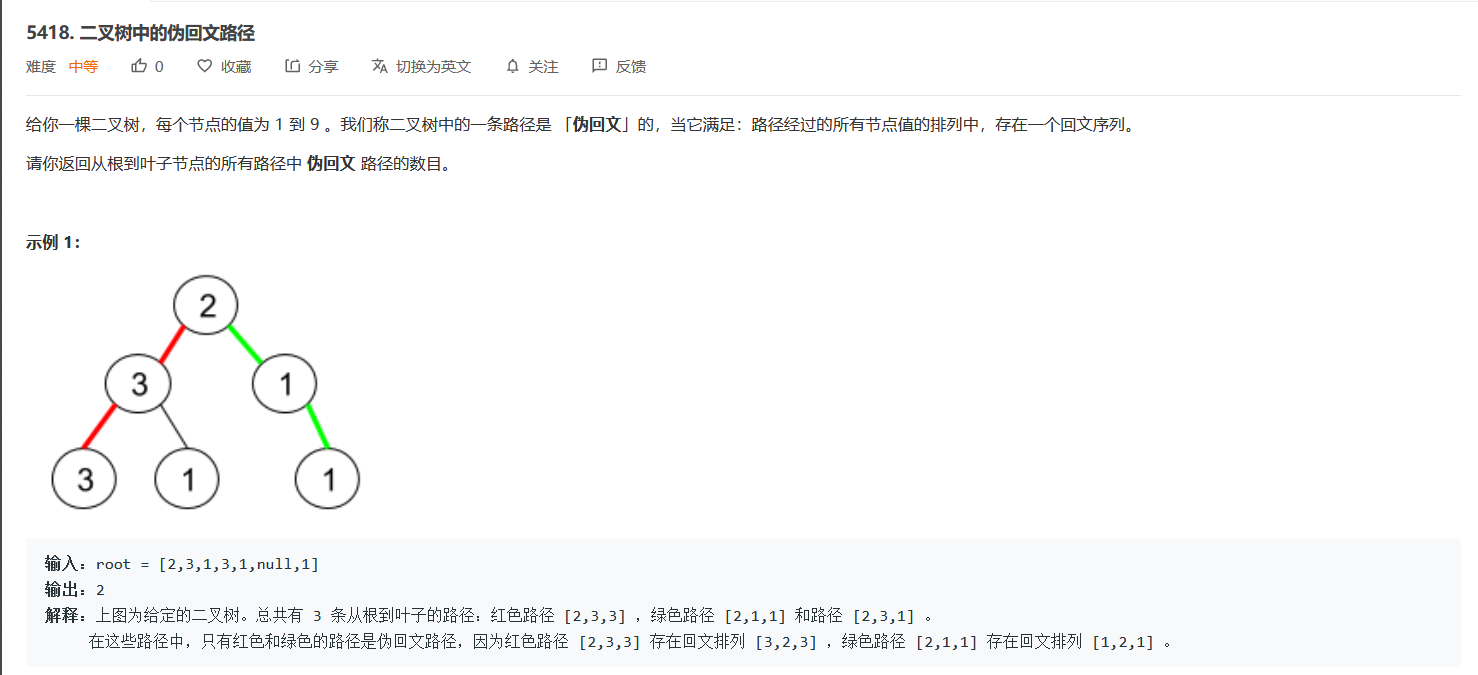
 DFS遍历二叉树，用数组进行记录，最后如果数字为奇数个的数目不超过1一个则是一种方案ans++。利用DFS进行回溯算法进行遍历，每次遍历到叶子节点进行判定。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
	int ans = 0;
    int pseudoPalindromicPaths (TreeNode* root) {
        for(int i = 0; i < 10; ++i) {
        	sb[i] = 0;
        }
        DFSS(root);
        return ans;
    }
    bool j(){
        int __ = 0;
        for(int i = 1; i < 10; i++) {
            if(sb[i] & 1 == 1) {
                __++;
            }
            if(__ > 1) {
            	return 0;
            }        	
        }
        return 1;
    }
    void DFSS(TreeNode* root){
        sb[root -> val]++;
        if(root -> left || root -> right){
            if(root -> left)
                DFSS(root -> left);
            if(root -> right)
                DFSS(root -> right);
        }
        else if(j())
            ans++;
        sb[root->val]--;
    }

private:
    int sb[10];
};

 

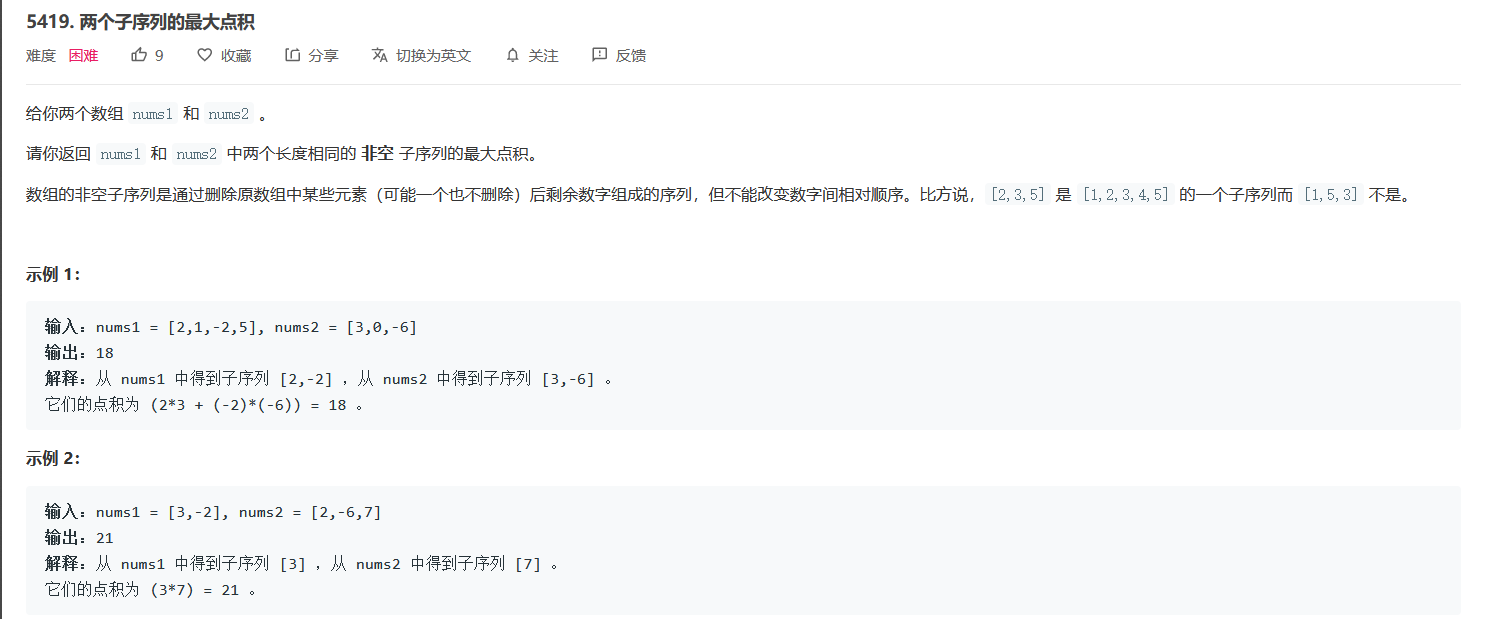
 一道很好的二维dp问题。关键在于找出状态转移方程：dp[i][j]代表nums1前i个和nums2前j的最优解。状态转移为一下五类的最大值   1.第i-1和第j-1个数相乘   2.第i-1和第j-1个数相乘+dp[i-1][j-1] 3.dp[i-1][j] 4.dp[i][j-1] 5.dp[i-1][j-1]。注意初始化为最小负数 最终结果为负数的情况会出错。

class Solution {
public:
	int dp[510][510];
    int maxDotProduct(vector<int>& nums1, vector<int>& nums2) {
        memset(dp, -0x3f3f3f3f, sizeof dp);
        // dp[1][1] = nums1[0] * nums2[0];
    	for(int i = 1; i <= nums1.size(); ++i) {
    		for(int j = 1; j <= nums2.size(); ++j) {
    			dp[i][j] = nums1[i - 1] * nums2[j - 1];
    			dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + dp[i][j]);
    			dp[i][j] = max(dp[i][j], dp[i - 1][j]);
    			dp[i][j] = max(dp[i][j], dp[i][j - 1]);
    			dp[i][j] = max(dp[i][j], dp[i - 1][j - 1]);
    		}
    	}
    	return dp[nums1.size()][nums2.size()];
    }
};