算法笔记_树形DP

一些前言：DP是个神奇的东西，有时候一些题看到要用DP，但是却因为没有思路而不会。属实挺遗憾的。今天学习学习树形DP，希望济南站能用到。

来道例题：HDU1520

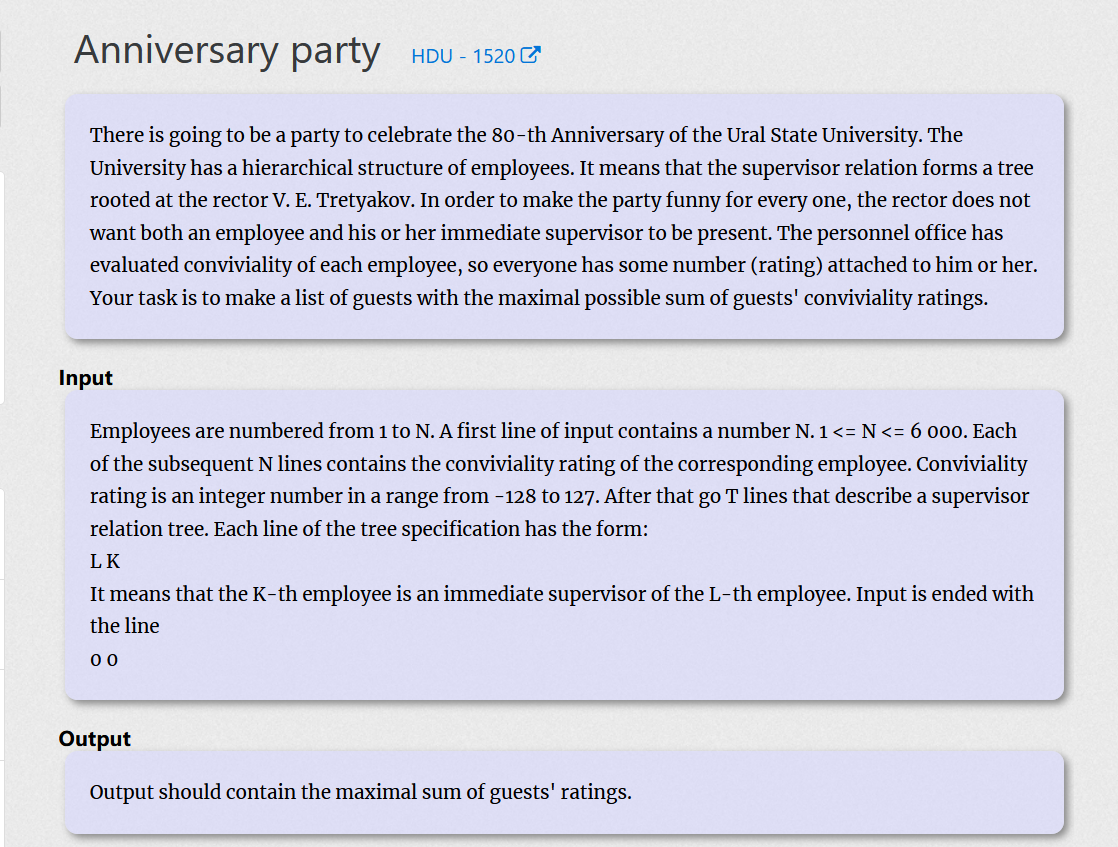
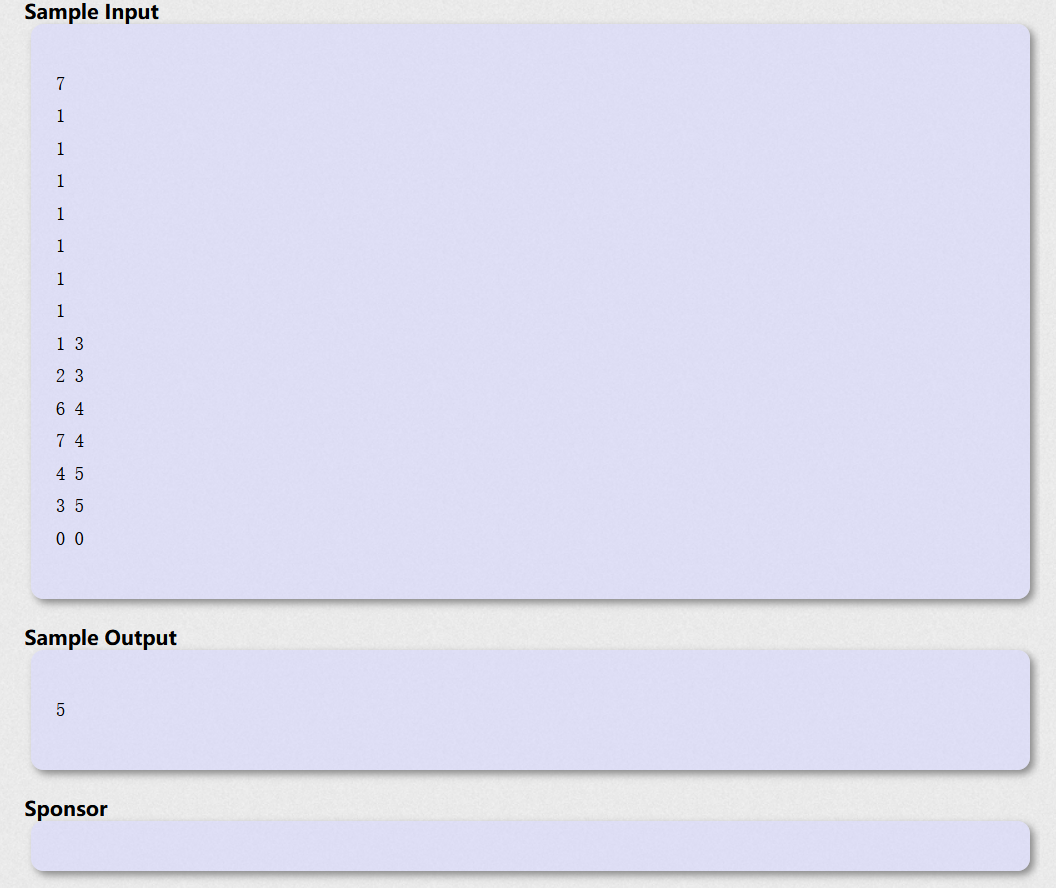
题意：如图中样例所示，我们可以构建出这样的树。

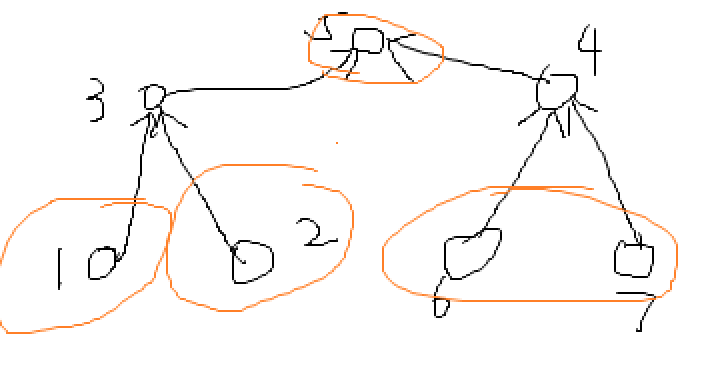
对于样例，显然我们选择画圈的部分可以使得整个收益最大。

本题的解题关键之处有两点：1.利用邻接表进行树的存储 2.确定状态转移方程：f[n][1] += f[上一个结点][0]和f[n][0] += max(f[上一个结点][1], f[上一个结点][0]);

一些细节：多输入，注意清空。代码如下：

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 60005;
struct  node
{
	int next, to;
}q[MAXN];

int head[MAXN], f[MAXN][3], book[MAXN], v[MAXN];

void dfs(int n) {
	v[n] = 1;
	for(int j = head[n] ; j != -1; j = q[j].next) {
		if(v[q[j].to] == 1) {
			continue;
		}
		dfs(q[j].to);
		f[n][1] += f[q[j].to][0];
		f[n][0] += max(f[q[j].to][1], f[q[j].to][0]);
	}
	return;
}
int main () {
	int n;
	while(cin >> n) {
		memset(head, -1, sizeof head);
		memset(f, 0, sizeof f);
		memset(book, 0, sizeof book);
		memset(q, 0, sizeof q);
		memset(v, 0, sizeof v);
		int l ,k;
		for(int i = 1; i <= n; ++i) {
			cin >> f[i][1];
		}
		int ii = 0;	
		while(cin >> l >> k && (l + k)) {
			ii++;
			q[ii].to = l;
			q[ii].next = head[k];
			head[k] = ii;
			book[l] = 1;
		}
		int u;
		for(int i = 1; i <= n; ++i) {
			if(book[i] == 0) {
				u = i;
				dfs(i);
				break;
			}
		}
		cout << max(f[u][1], f[u][0]) << endl;		
	}
}

如果你以为树上DP九折水瓶，那可就大错特错了，下面来道难的

HDU2196

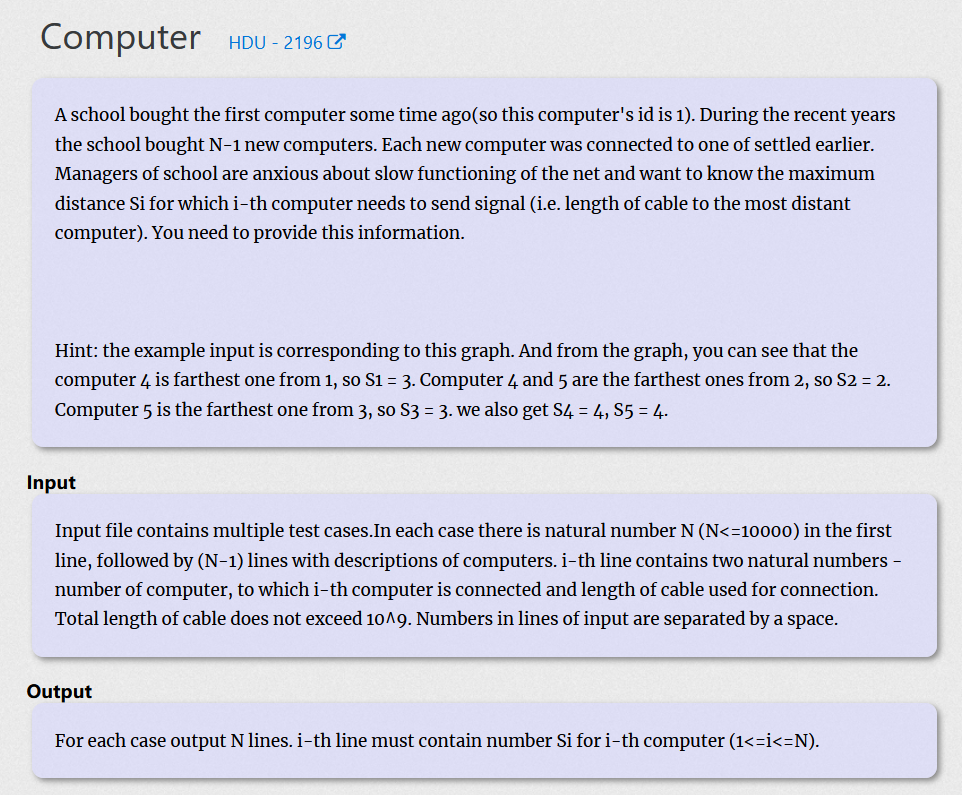
该题要求求解出树上最长距离（即求出树的直径）