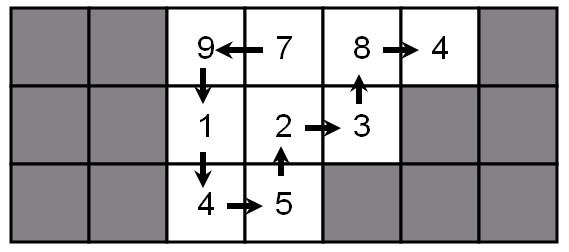
如图,给一个图,每个格子只能走一次,起点终点任意,求按路径顺序将格子里的数字拼在一起,最大的数字。
很容易想到用暴力求解的方法,但最多会有 30 个格子,O(2^30) 肯定超时了。
考虑剪枝,设当前已经找到一个 ans,若当前路径的最大长度小于 ans 的长度,则不可能比 ans 大,剪掉, 若等于,则考虑当前路径已经形成的数字(假设 n 位),若小于 ans 的前 n 位,则剪掉。
代码:
#include <iostream> #include <cstring> #include <queue> #include <vector> #include <algorithm> using namespace std; const int MAX = 20;int dx[4] = {-1, 0, 1, 0}; int dy[4] = { 0, 1, 0,-1}; char G[MAX][MAX]; int vis[MAX][MAX]; int vis2[MAX][MAX]; string ans; int r, c; void dfs(int i, int j, string sum); //暴力求解 int getLen(int i, int j); //求在 i,j点开始走,最长的路径是多少 string maxSum(string s1, string s2); //比较两个数字 int main(){ freopen("input.txt", "r", stdin); while(cin >> r >> c){ if(r == 0 && c == 0) break; for(int i=1; i<=r; i++){ for(int j=1; j<=c; j++){ cin >> G[i][j]; } } ans = ""; for(int i=1; i<=r; i++){ for(int j=1; j<=c; j++){ if(G[i][j] != '#'){ memset(vis, 0, sizeof(vis)); dfs(i, j, ""); } } } cout << ans << endl; } return 0; } void dfs(int i, int j, string sum){ if(vis[i][j] == 1) return ; sum = sum + G[i][j]; memcpy(vis2, vis, sizeof(vis)); int len = getLen(i, j) - 1; if(len + sum.length() < ans.length()){ //长度不够 return ; } if(len + sum.length() == ans.length()){ //长度相同,但不可能比答案更大 if(sum < ans.substr(0, sum.length())) return ; } if(len == 0){ //更新一个答案 ans = maxSum(ans, sum); return ; } vis[i][j] = 1; for(int k=0; k<4; k++){ int x = i + dx[k], y = j + dy[k]; if(x < 1 || x > r || y < 1 || y > c || G[x][y] == '#' || vis[x][y] == 1){ continue; }else{ dfs(x, y, sum); } } vis[i][j] = 0; } int getLen(int i, int j){ if(vis2[i][j] == 1) return 0; vis2[i][j] = 1; int sum = 1; for(int k=0; k<4; k++){ int x = i + dx[k]; int y = j + dy[k]; if(x < 1 || x > r || y < 1 || y > c || vis2[x][y] || G[x][y] == '#') continue; sum += getLen(x, y); } return sum; } string maxSum(string s1, string s2){ if(s1.length() == s2.length()) return max(s1, s2); else{ if(s1.length() > s2.length()) return s1; return s2; } }