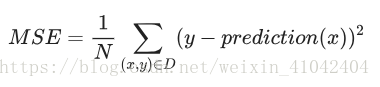目录
一、机器学习简介 (Introduction to Machine Learning)
三、深入了解机器学习 (Descending into ML)
经验风险最小化(ERM, empirical risk minimization)
结构风险最小化 (SRM, structural risk minimization)
随机梯度下降法 (SGD, stochastic gradient descent)
小批量随机梯度下降法 (SGD, mini-batch stochastic gradient descent)
一、机器学习简介 (Introduction to Machine Learning)
- 样本是指数据的特定实例:x
- 有标签样本具有 {特征, 标签}:(x, y)
- 用于训练模型
- 无标签样本具有 {特征, ?}:(x, ?)
- 用于对新数据做出预测
- 模型可将样本映射到预测标签:y'
- 由模型的内部参数定义,这些内部参数值是通过学习得到的
二、问题构建 (Framing)
基本框架:
监督式机器学习
非监督式机器学习
在监督式机器学习中, 我们将学习如何创建模型来结合输入信息, 对以前从未见过的数据做出有用的预测。
当我们训练该模型时,会为其提供标签。以垃圾邮件过滤模型为例,标签可以是 “垃圾邮件或非垃圾邮件”等内容,它是我们试图预测的目标。
特征是我们表示数据的方式。特征可以从电子邮件中提取,例如, 电子邮件中的字词、“收件人和发件人地址”、各种路由或标题信息, 以及任何可以从电子邮件中提取并提供给机器学习系统的信息。
样本是一份数据。例如,一封电子邮件。它可以是有标签的样本, 其中包含电子邮件中呈现的特征信息, 以及标签值“垃圾邮件或非垃圾邮件”。这些信息可能来自用户。或者,它也可以是无标签样本, 例如,一封我们拥有关于它的特征信息、 但不知道它是否为垃圾邮件的电子邮件。我们要做的很可能是对其进行分类, 将其放入用户的收件箱或“垃圾邮件”文件夹。
最后,我们会获得一个模型, 该模型是执行预测的工具。我们将通过从数据中学习规律这一过程来尝试创建模型。
什么是(监督式)机器学习?简单来说,它的定义如下:
- 机器学习系统通过学习如何组合输入信息来对从未见过的数据做出有用的预测。
标签(label)
标签是我们要预测的事物,即简单线性回归中的
y变量。标签可以是小麦未来的价格、图片中显示的动物品种、音频剪辑的含义或任何事物。
特征 (feature)
特征是输入变量,即简单线性回归中的
x变量。简单的机器学习项目可能会使用单个特征,而比较复杂的机器学习项目可能会使用数百万个特征,按如下方式指定:{x1,x2,...xN}在垃圾邮件检测器示例中,特征可能包括:
- 电子邮件文本中的字词
- 发件人的地址
- 发送电子邮件的时段
- 电子邮件中包含“一种奇怪的把戏”这样的短语。
样本(example)
样本是数据集的一行,指数据的特定实例:x。(我们采用粗体 x 表示它是一个矢量。)我们将样本分为以下两类:
- 有标签样本 (labeled example)
- 无标签样本(unlabeled example)
有标签样本同时包含特征和标签。即:
labeled examples: {features, label}: (x, y)我们使用有标签样本来训练模型。在我们的垃圾邮件检测器示例中,有标签样本是用户明确标记为“垃圾邮件”或“非垃圾邮件”的各个电子邮件。
例如,下表显示了从包含加利福尼亚州房价信息的数据集中抽取的 5 个有标签样本:
housingMedianAge
(特征)totalRooms
(特征)totalBedrooms
(特征)medianHouseValue
(标签)15 5612 1283 66900 19 7650 1901 80100 17 720 174 85700 14 1501 337 73400 20 1454 326 65500
无标签样本包含特征,但不包含标签。即:
unlabeled examples: {features, ?}: (x, ?)在使用有标签样本训练了我们的模型之后,我们会使用该模型来预测无标签样本的标签。在垃圾邮件检测器示例中,无标签样本是用户尚未添加标签的新电子邮件。
模型 (model)
机器学习系统从训练数据学到的内容的表示形式。多含义术语,可以理解为下列两种相关含义之一:
- 一种 TensorFlow 图,用于表示预测计算结构。
- 该 TensorFlow 图的特定权重和偏差,通过训练决定。
模型定义了特征与标签之间的关系。例如,垃圾邮件检测模型可能会将某些特征与“垃圾邮件”紧密联系起来。我们来重点介绍一下模型生命周期的两个阶段:
-
训练 (training)表示创建或学习模型。确定最佳模型的过程。也就是说,您向模型展示有标签样本,让模型逐渐学习特征与标签之间的关系。
-
推断 (inference)表示将训练后的模型应用于无标签样本。也就是说,您使用训练后的模型来做出有用的预测 (
y')。例如,在推断期间,您可以针对新的无标签样本预测medianHouseValue。在统计学中,推断是指在某些观测数据条件下拟合分布参数的过程。(请参阅维基百科中有关统计学推断的文章。)
回归与分类
回归模型 (regression model)可预测连续值。例如,回归模型做出的预测可回答如下问题:
加利福尼亚州一栋房产的价值是多少?
用户点击此广告的概率是多少?
分类模型(classification model)可预测离散值。例如,分类模型做出的预测可回答如下问题:
某个指定电子邮件是垃圾邮件还是非垃圾邮件?
这是一张狗、猫还是仓鼠图片?
三、深入了解机器学习 (Descending into ML)
1.线性回归(linear regression)
一种回归模型,通过将输入特征进行线性组合,以连续值作为输出。
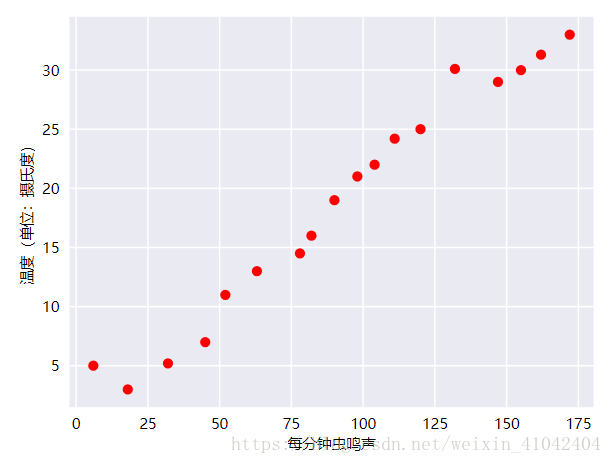
人们早就知晓,相比凉爽的天气,蟋蟀在较为炎热的天气里鸣叫更为频繁。数十年来,专业和业余昆虫学者已将每分钟的鸣叫声和温度方面的数据编入目录。Ruth 阿姨将她喜爱的蟋蟀数据库作为生日礼物送给您,并邀请您自己利用该数据库训练一个模型,从而预测鸣叫声与温度的关系。
首先建议您将数据绘制成图表,了解下数据的分布情况:
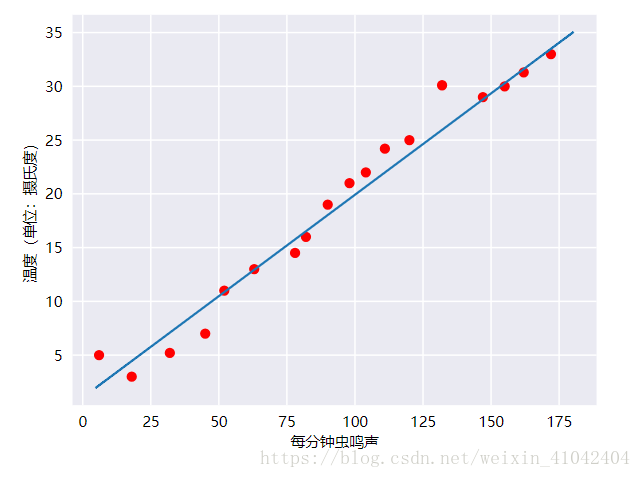
毫无疑问,此曲线图表明温度随着鸣叫声次数的增加而上升。鸣叫声与温度之间的关系是线性关系吗?是的,您可以绘制一条直线来近似地表示这种关系,如下所示:
事实上,虽然该直线并未精确无误地经过每个点,但针对我们拥有的数据,清楚地显示了鸣叫声与温度之间的关系。只需运用一点代数知识,您就可以将这种关系写下来,如下所示:
y=mx+b
其中:
- y 指的是温度(以摄氏度表示),即我们试图预测的值。
- m 指的是直线的斜率。
- x 指的是每分钟的鸣叫声次数,即输入特征的值。
- b 指的是 y 轴截距。
按照机器学习的惯例,您需要写一个存在细微差别的模型方程式:
y′=b+w1x1
其中:
- y′ 指的是预测标签(理想输出值)。
- b 指的是偏差 (bias)(y 轴截距)。而在一些机器学习文档中,它称为 w0。
- w1 指的是特征 1 的权重(weight)。权重与上文中用 m 表示的“斜率”的概念相同。线性模型中特征的系数,或深度网络中的边。训练线性模型的目标是确定每个特征的理想权重。如果权重为 0,则相应的特征对模型来说没有任何贡献。
- x1 指的是特征(已知输入项)。
要根据新的每分钟的鸣叫声值 x1 推断(预测)温度 y′,只需将 x1 值代入此模型即可。
下标(例如 w1 和 x1)预示着可以用多个特征来表示更复杂的模型。例如,具有三个特征的模型可以采用以下方程式:
y′=b+w1x1+w2x2+w3x3
2.训练与损失
简单来说,训练模型表示通过有标签样本来学习(确定)所有权重和偏差的理想值。
在监督式学习中,机器学习算法通过以下方式构建模型:检查多个样本并尝试找出可最大限度地减少损失的模型;这一过程称为经验风险最小化(ERM, empirical risk minimization)。
经验风险最小化(ERM, empirical risk minimization)
用于选择可以将基于训练集的损失降至最低的模型函数。与结构风险最小化相对。
结构风险最小化 (SRM, structural risk minimization)
一种算法,用于平衡以下两个目标:
- 期望构建最具预测性的模型(例如损失最低)。
- 期望使模型尽可能简单(例如强大的正则化)。
例如,旨在将基于训练集的损失和正则化降至最低的模型函数就是一种结构风险最小化算法。
损失是对糟糕预测的惩罚。也就是说,损失是一个数值,表示对于单个样本而言模型预测的准确程度。如果模型的预测完全准确,则损失为零,否则损失会较大。训练模型的目标是从所有样本中找到一组平均损失“较小”的权重和偏差。
损失 (Loss)
一种衡量指标,用于衡量模型的预测偏离其标签的程度。或者更悲观地说是衡量模型有多差。要确定此值,模型必须定义损失函数。例如,线性回归模型通常将均方误差用于损失函数,而逻辑回归模型则使用对数损失函数。
例如,图 3 左侧显示的是损失较大的模型,右侧显示的是损失较小的模型。关于此图,请注意以下几点:
- 红色箭头表示损失。
- 蓝线表示预测。
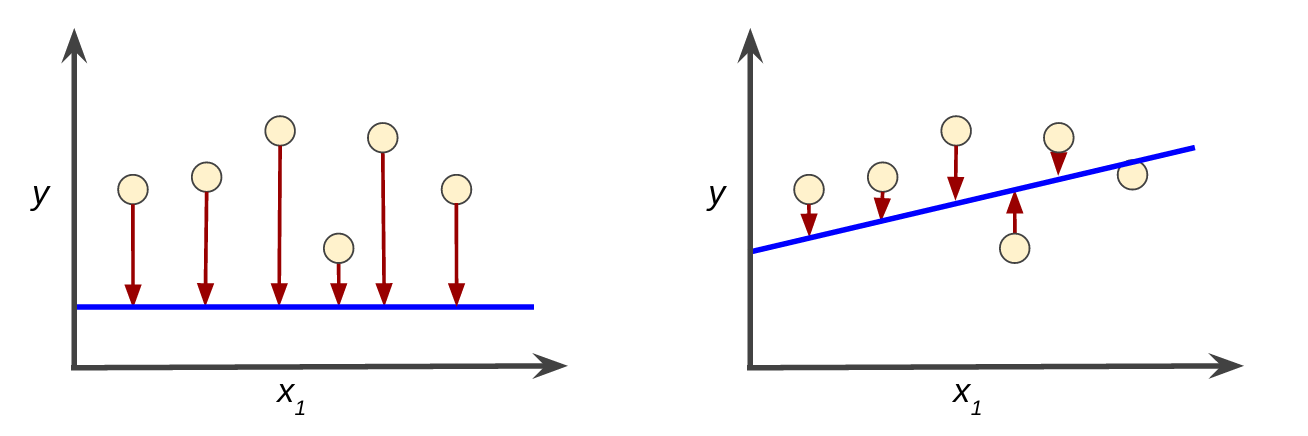
图 3. 左侧模型的损失较大;右侧模型的损失较小。
请注意,左侧曲线图中的红色箭头比右侧曲线图中的对应红色箭头长得多。显然,相较于左侧曲线图中的蓝线,右侧曲线图中的蓝线代表的是预测效果更好的模型。
您可能想知道自己能否创建一个数学函数(损失函数),以有意义的方式汇总各个损失。
L1 损失函数 (L₁ loss)
一种损失函数,基于模型预测的值与标签的实际值之差的绝对值。与 L2 损失函数相比,L1 损失函数对离群值的敏感性弱一些。
平方损失(squared loss)( L2 损失)
该函数可计算模型为有标签样本预测的值和标签的实际值之差的平方。由于取平方值,因此该损失函数会放大不佳预测的影响。与 L1 损失函数相比,平方损失函数对离群值的反应更强烈。
接下来我们要看的线性回归模型使用的是一种称为平方损失的损失函数。单个样本的平方损失如下:
= the square of the difference between the label and the prediction
= (observation - prediction(x))2
= (y - y')2
均方误差(MSE, Mean Squared Error)
每个样本的平均平方损失。要计算 MSE,请求出各个样本的所有平方损失之和,然后除以样本数量。
TensorFlow Playground 显示的“训练损失”值和“测试损失”值都是 MSE。
- (x,y) 指的是样本,其中
- x 指的是模型进行预测时使用的特征集(例如,温度、年龄和交配成功率)。
- y 指的是样本的标签(例如,每分钟的鸣叫次数)。
- prediction(x) 指的是权重和偏差与特征集 x 结合的函数。
- D 指的是包含多个有标签样本(即 (x,y))的数据集。
- N 指的是 D 中的样本数量。
虽然 MSE 常用于机器学习,但它既不是唯一实用的损失函数,也不是适用于所有情形的最佳损失函数。
四、降低损失 (Reducing Loss)
为了训练模型,我们需要一种可降低模型损失的好方法。迭代方法是一种广泛用于降低损失的方法,而且使用起来简单有效。
1.迭代方法
迭代学习可能会让您想到“Hot and Cold”这种寻找隐藏物品(如顶针)的儿童游戏。在我们的游戏中,“隐藏的物品”就是最佳模型。刚开始,您会胡乱猜测(“w1 的值为 0。”),等待系统告诉您损失是多少。然后,您再尝试另一种猜测(“w1 的值为 0.5。”),看看损失是多少。哎呀,这次更接近目标了。实际上,如果您以正确方式玩这个游戏,通常会越来越接近目标。这个游戏真正棘手的地方在于尽可能高效地找到最佳模型。
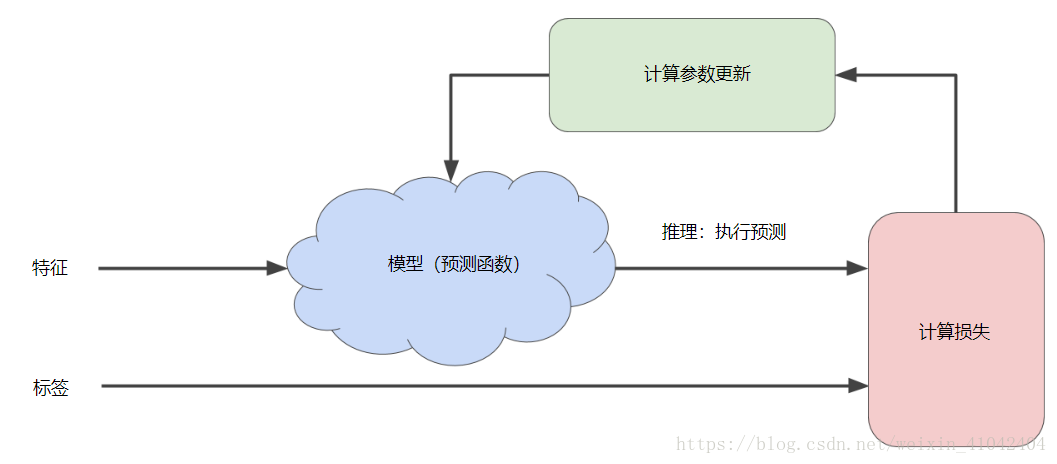
下图显示了机器学习算法用于训练模型的迭代试错过程:
图 1. 用于训练模型的迭代方法。
我们将在整个机器学习速成课程中使用相同的迭代方法详细说明各种复杂情况,尤其是处于暴风雨中的蓝云区域。迭代策略在机器学习中的应用非常普遍,这主要是因为它们可以很好地扩展到大型数据集。
“模型”部分将一个或多个特征作为输入,然后返回一个预测 (y') 作为输出。为了进行简化,不妨考虑一种采用一个特征并返回一个预测的模型:y′=b+w1x1
我们应该为 b 和 w1 设置哪些初始值?对于线性回归问题,事实证明初始值并不重要。我们可以随机选择值,不过我们还是选择采用以下这些无关紧要的值:
- b = 0
- w1 = 0
假设第一个特征值是 10。将该特征值代入预测函数会得到以下结果:
y' = 0 + 0(10)
y' = 0
图中的“计算损失”部分是模型将要使用的损失函数。假设我们使用平方损失函数。损失函数将采用两个输入值:
- y':模型对特征 x 的预测
- y:特征 x 对应的正确标签。
最后,我们来看图的“计算参数更新”部分。机器学习系统就是在此部分检查损失函数的值,并为 b 和 w1 生成新值。现在,假设这个神秘的绿色框会产生新值,然后机器学习系统将根据所有标签重新评估所有特征,为损失函数生成一个新值,而该值又产生新的参数值。这种学习过程会持续迭代,直到该算法发现损失可能最低的模型参数。通常,您可以不断迭代,直到总体损失不再变化或至少变化极其缓慢为止。这时候,我们可以说该模型已收敛。
收敛(convergence)
通俗来说,收敛通常是指在训练期间达到的一种状态,即经过一定次数的迭代之后,训练损失和验证损失在每次迭代中的变化都非常小或根本没有变化。也就是说,如果采用当前数据进行额外的训练将无法改进模型,模型即达到收敛状态。在深度学习中,损失值有时会在最终下降之前的多次迭代中保持不变或几乎保持不变,暂时形成收敛的假象。
另请参阅早停法。
另请参阅 Boyd 和 Vandenberghe 合著的 Convex Optimization(《凸优化》)。
早停法 (early stopping)
一种正则化方法,涉及在训练损失仍可以继续减少之前结束模型训练。使用早停法时,您会在基于验证数据集的损失开始增加(也就是泛化效果变差)时结束模型训练。
要点:
在训练机器学习模型时,首先对权重和偏差进行初始猜测,然后反复调整这些猜测,直到获得损失可能最低的权重和偏差为止。
2.梯度下降法
梯度下降法是迭代方法中的一种实质的“计算参数更新”的算法。
损失函数收敛点
假设我们有时间和计算资源来计算 w1 的所有可能值的损失。
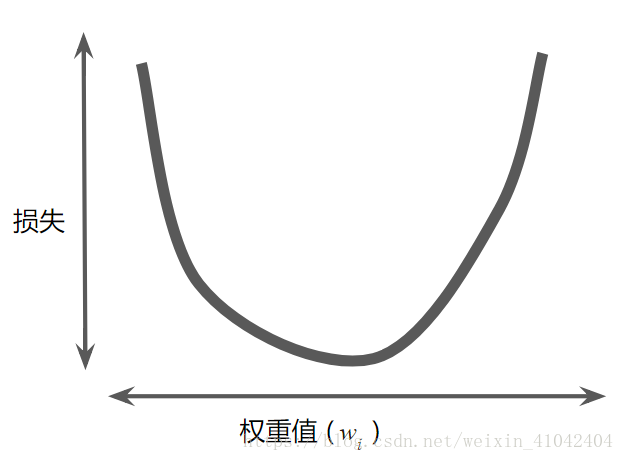
对于我们一直在研究的回归问题,所产生的损失与 w1 的图形始终是凸形。换言之,图形始终是碗状图,如下所示:
图 2. 回归问题产生的损失与权重图为凸形。
凸形问题只有一个最低点;即只存在一个斜率正好为 0 的位置。这个最小值就是损失函数收敛之处。
通过计算整个数据集中 w1 每个可能值的损失函数来找到收敛点这种方法效率太低。我们来研究一种更好的机制,这种机制在机器学习领域非常热门,称为梯度下降法。
梯度下降法 (gradient descent)
一种通过计算梯度并且减小梯度将损失降至最低的技术。它以训练数据为条件,来计算损失相对于模型参数的梯度,以迭代方式调整参数,逐渐找到权重和偏差的最佳组合,从而将损失降至最低。
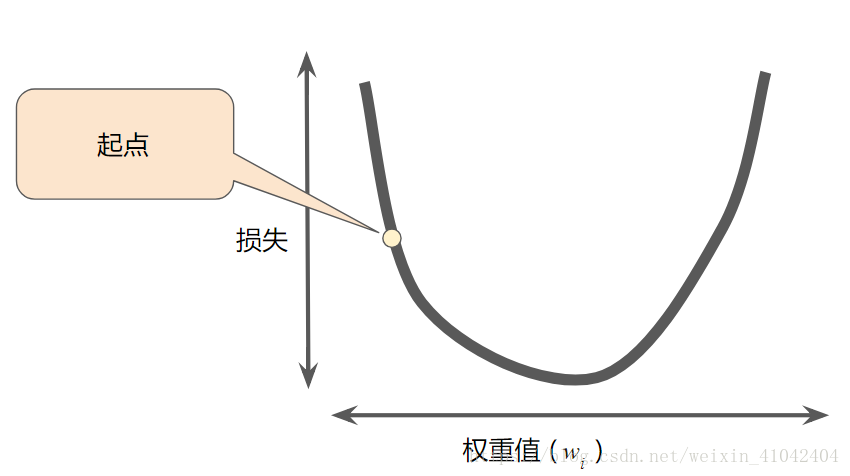
1.梯度下降法的第一个阶段是为 w1 选择一个起始值(起点)。起点并不重要;因此很多算法就直接将 w1 设为 0 或随机选择一个值。下图显示的是我们选择了一个稍大于 0 的起点:
图 3. 梯度下降法的起点。
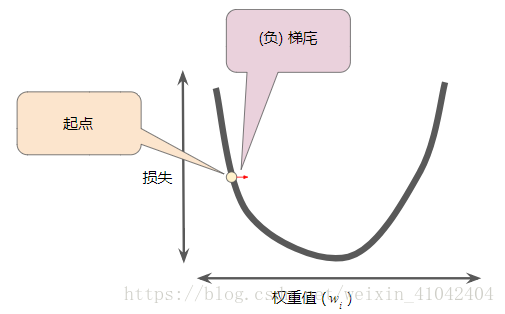
2.梯度下降法算法会计算损失曲线在起点处的梯度。梯度是偏导数的矢量;它可以让您了解哪个方向距离目标“更近”或“更远”。损失相对于单个权重的梯度(如图 3 所示)就等于导数。
偏导数
多变量函数指的是具有多个参数的函数,例如:
f 相对于 x 的偏导数表示如下:
是 f (x) 的导数。
要计算f 相对于 x 的偏导数:您必须使 y 保持固定不变(因此 f 现在是只有一个变量 x 的函数),然后取 f 相对于 x 的常规导数。
例如,当 y 固定为 1 时,前面的函数变为:
这只是一个变量 x 的函数,其导数为:
一般来说,假设 y 保持不变,f 对 x 的偏导数的计算公式如下:
同样,如果我们使 x 保持不变,f 对 y 的偏导数为:
直观而言,偏导数可以让您了解到,当您略微改动一个变量时,函数会发生多大的变化。在前面的示例中:
因此,如果您将起点设为 (0,1),使 y 保持固定不变并将 x 移动一点,f 的变化量将是 x 变化量的 7.4 倍左右。
在机器学习中,偏导数主要与函数的梯度一起使用。
梯度(gradient)
偏导数相对于所有自变量的向量。表示如下:
。
例如,如果:
。则:
在机器学习中,梯度是模型函数偏导数的向量。梯度指向最速上升的方向。
梯度是一个矢量,因此具有以下两个特征:方向。大小。请注意以下几点:
∇f
指向函数增长速度最快的方向。 −∇f
指向函数下降速度最快的方向。 该矢量中的维度个数等于 f 公式中的变量个数;换言之,该矢量位于该函数的域空间内。
例如,在三维空间中查看下面的函数 f(x,y) 时:
。z = f(x,y) 就像一个山谷,最低点为 (2,0,4):
f(x,y) 的梯度是一个二维矢量,可让您了解向哪个 (x,y) 方向移动时高度下降得最快。也就是说,梯度矢量指向山谷。
在机器学习中,梯度用于梯度下降法。我们的损失函数通常具有很多变量,而我们尝试通过跟随函数梯度的负方向来尽量降低损失函数。
3.梯度始终指向损失函数中增长最为迅猛的方向。梯度下降法算法会沿着负梯度的方向走一步,以便尽快降低损失。
图 4. 梯度下降法依赖于负梯度。
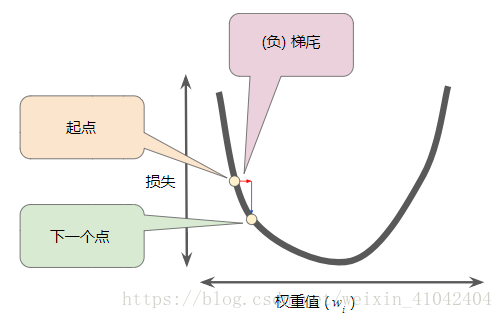
4.为了确定损失函数曲线上的下一个点,梯度下降法算法会将梯度大小的一部分与起点相加,如下图所示:
图 5. 一个梯度步长将我们移动到损失曲线上的下一个点。
然后,梯度下降法会重复此过程,逐渐接近最低点。
步 (step)
对一个批次的向前和向后评估。
步长 (step size)
是学习速率的同义词。
梯度步长 (gradient step size)
梯度乘以学习速率。
3.学习速率
正如之前所述,梯度矢量具有方向和大小。梯度下降法算法用梯度乘以一个称为学习速率(有时也称为步长)的标量,以确定下一个点的位置。
例如,如果梯度大小为 2.5,学习速率为 0.01,则梯度下降法算法会选择距离前一个点 0.025 的位置作为下一个点。
学习速率 (learning rate)
在训练模型时用于梯度下降的一个变量。
在每次迭代期间,梯度下降法都会将学习速率与梯度相乘,得出的乘积称为梯度步长。
超参数 (hyperparameter)
编程人员在模型训练的连续过程中,调节的“旋钮”。比如,调整学习速率。学习速率是一个重要的超参数。
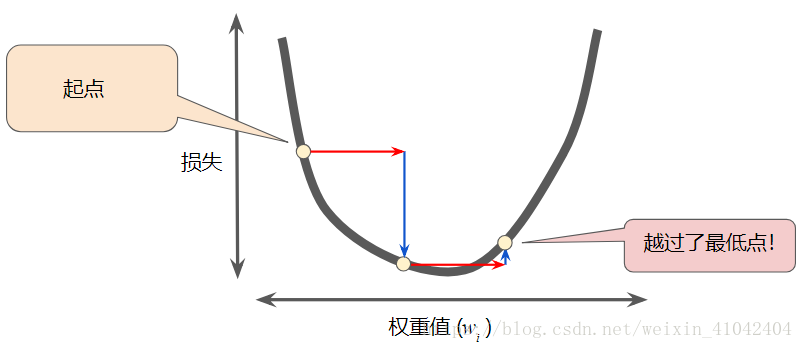
例如,学习速率就是一种超参数。与参数相对。如果您选择的学习速率过小,就会花费太长的学习时间:
图 6. 学习速率过小。
相反,如果您指定的学习速率过大,下一个点将永远在 U 形曲线的底部随意弹跳,就好像量子力学实验出现了严重错误一样:
图 7. 学习速率过大。
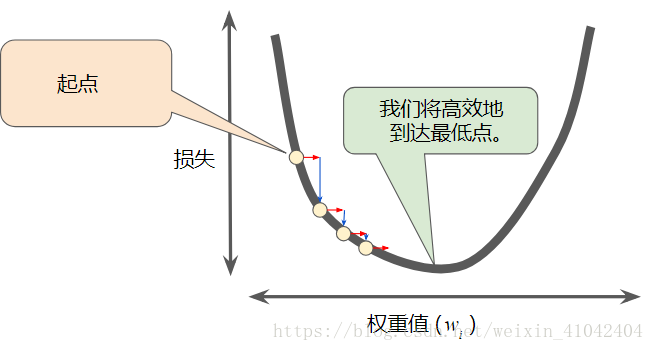
每个回归问题都存在一个金发姑娘学习速率。“金发姑娘”值与损失函数的平坦程度相关。如果您知道损失函数的梯度较小,则可以放心地试着采用更大的学习速率,以补偿较小的梯度并获得更大的步长。
图 8. 学习速率恰恰好。
4.优化学习速率
尝试不同的学习速率,看看不同的学习速率对到达损失曲线最低点所需的步数有何影响。
练习 1:在滑块上设置 0.1 的学习速率。不断按下“STEP”(步)按钮,直到梯度下降法算法到达损失曲线的最低点。一共走了多少步?
答案:梯度下降法到达曲线的最低点需要 81 步。
练习 2:您可以使用更高的学习速率更快地到达最低点吗?将学习速率设为 1,然后不断按“STEP”(步)按钮,直到梯度下降法到达最低点。这次走了多少步?
答案:梯度下降法到达曲线的最低点需要 6 步。
练习 3:如果采用更大的学习速率会怎么样?重置该图,将学习速率设为 4,然后尝试到达损失曲线的最低点。这次发生了什么情况?
答案:梯度下降法从未到达最低点。结果是,步长逐渐增加。每一步都在曲线上来回跳跃,沿着曲线向上爬,而不是降到底部。
可选挑战:您能否为该曲线找到金发姑娘般刚刚好的学习速率,让梯度下降法以最少的步数到达最低点?最少需要多少步才能到达最低点?
答案:该数据的“金发姑娘般刚刚好”的学习速率为 1.6,1 步就能到达最低点。
注意:在实践中,成功的模型训练并不意味着要找到“完美”(或接近完美)的学习速率。我们的目标是找到一个足够高的学习速率,该速率要能够使梯度下降过程高效收敛,但又不会高到使该过程永远无法收敛。
5.随机梯度下降法
批量 (batch)
在梯度下降法中,批量指的是用于在单次迭代中计算梯度的样本总数。
批量规模 (batch size)
一个批量中的样本数。例如,SGD 的批次规模为 1,而小批次的规模通常介于 10 到 1000 之间。
批次规模在训练和推断期间通常是固定的;不过,TensorFlow 允许使用动态批次规模。
到目前为止,我们一直假定批量是指整个数据集。就 Google 的规模而言,数据集通常包含数十亿甚至数千亿个样本。此外,Google 数据集通常包含海量特征。因此,一个批量可能相当巨大。如果是超大批量,则单次迭代就可能要花费很长时间进行计算。包含随机抽样样本的大型数据集可能包含冗余数据。实际上,批量大小越大,出现冗余的可能性就越高。一些冗余可能有助于消除杂乱的梯度,但超大批量所具备的预测价值往往并不比大型批量高。如果我们可以通过更少的计算量得出正确的平均梯度,会怎么样?通过从我们的数据集中随机选择样本,我们可以通过小得多的数据集估算(尽管过程非常杂乱)出较大的平均值。
随机梯度下降法 (SGD, stochastic gradient descent)
批次规模为 1 的一种梯度下降法。如果进行足够的迭代,SGD 也可以发挥作用,但过程会非常杂乱。“随机”这一术语表示构成各个批量的一个样本都是随机选择的。也就是说,SGD 依赖于从数据集中随机均匀选择的单个样本来计算每步的梯度估算值。
小批次 (mini-batch)
从训练或推断过程的一次迭代中一起运行的整批样本内随机选择的一小部分。小批次的规模通常介于 10 到 1000 之间。与基于完整的训练数据计算损失相比,基于小批次数据计算损失要高效得多。
小批量随机梯度下降法 (SGD, mini-batch stochastic gradient descent)
一种采用小批次样本的梯度下降法。也就是说,小批次 SGD 会根据一小部分训练数据来估算梯度。Vanilla SGD 使用的小批次的规模为 1。是介于全批量迭代与 SGD 之间的折衷方案。小批量 SGD 可以减少 SGD 中的杂乱样本数量,但仍然比全批量更高效。