POJ 2488：A Knight's Journey 深搜入门之走马观花

A Knight's Journey

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 35342		Accepted: 12051

Description

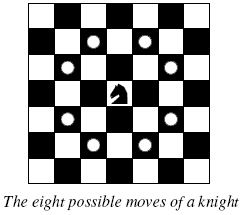
Background 
The knight is getting bored of seeing the same black and white squares again and again and has decided to make a journey 
around the world. Whenever a knight moves, it is two squares in one direction and one square perpendicular to this. The world of a knight is the chessboard he is living on. Our knight lives on a chessboard that has a smaller area than a regular 8 * 8 board, but it is still rectangular. Can you help this adventurous knight to make travel plans? 

Problem 
Find a path such that the knight visits every square once. The knight can start and end on any square of the board.

Input

The input begins with a positive integer n in the first line. The following lines contain n test cases. Each test case consists of a single line with two positive integers p and q, such that 1 <= p * q <= 26. This represents a p * q chessboard, where p describes how many different square numbers 1, . . . , p exist, q describes how many different square letters exist. These are the first q letters of the Latin alphabet: A, . . .

Output

The output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Then print a single line containing the lexicographically first path that visits all squares of the chessboard with knight moves followed by an empty line. The path should be given on a single line by concatenating the names of the visited squares. Each square name consists of a capital letter followed by a number. 
If no such path exist, you should output impossible on a single line.

Sample Input

3
1 1
2 3
4 3

Sample Output

Scenario #1:
A1

Scenario #2:
impossible

Scenario #3:
A1B3C1A2B4C2A3B1C3A4B2C4

给一个棋盘，给你一匹马，马只能走“日”字格，问马能否不重复地走完所有格并且输出其走的位置的字典顺序。

头一次做深搜，中间出了不少问题，包括color在深搜之后居然没给它还原回去，这样的错误也行。。。

然后字典顺序是一个，如何记录结果path路径。

深搜给我的第一个感受就是能不用全局变量就不用全局变量，总在这里容易出错，另外，记录走的步数要设立一个参数step，之后再每层加1，这样的做法才是正途。。。

稀里糊涂地说了这么多，都是自己当时犯下的错，各种辛酸只有自己明白了。。。

代码：

#include <iostream>
#include <algorithm>
#include <cmath>
#include <vector>
#include <string>
#include <cstring>
#pragma warning(disable:4996)
using namespace std;

struct struct_a{
	int x;
	int y;
}path[900];

int Test,i,p,q,m,n,flag,num;
int move_x[10]={-1,1,-2,2,-2,2,-1,1};//改成字典顺序
int move_y[10]={-2,-2,-1,-1,1,1,2,2};

int color[30][30];

int dfs(int a,int b,int step)
{
	if(flag==1)
		return 1;
	int k,temp_x,temp_y;
	if(step==q*p)
	{
		flag=1;
		return 1;
	}
	for(k=0;k<8;k++)
	{
		temp_x = a + move_x[k];
		temp_y = b + move_y[k];

		if(temp_x>=1 && temp_x<=p && temp_y>=1 && temp_y<=q && color[temp_x][temp_y]==0)
		{
			color[temp_x][temp_y] = color[a][b]+1;
			path[step].x=temp_x;//别用其他变量标记，递归这样不容易出现问题
			path[step].y=temp_y;
			dfs(temp_x,temp_y,step+1);
			if(flag)
				return 1;
		}
	}
	color[a][b]=0;//如果最终选择不是这里，要记得清空
	return 0;
}

int main()
{
	cin>>Test;

	for(i=1;i<=Test;i++)
	{
		cin>>p>>q;
		cout<<"Scenario #"<<i<<":"<<endl;

		flag=0;
		memset(color,0,sizeof(color));
		color[1][1]=1;
		path[0].x=1;
		path[0].y=1;

		dfs(1,1,1);

		if(flag==1)
		{
			int v;
			for(v=0;v<p*q;v++)
			{
				char temp_c=path[v].y-1+'A';
				cout<<temp_c<<path[v].x;
			}
			cout<<endl;
		}
		else
			cout<<"impossible"<<endl;
		cout<<endl;
	}

	return 0;
}

版权声明：本文为博主原创文章，未经博主允许不得转载。