题目链接:Happy Necklace HDU - 6030
华师男想为他的女朋友买一条项链。项链是由多个红色和蓝色珠子组成的单串。
身为华师男他体贴地想要更加打动他的女朋友,他知道,只要这段珠子中任意取出长度为质数的一段,都满足红珠数不少于蓝珠数,她就会喜欢这条项链。
现在,他想买一串纯正的有n个珠子的项链。他想知道满足条件的可以使他的女朋友更加开心的不同项链的数量。
注意:项链是一长串的 ,无需考虑首尾相连的珠子。.
Input
输入的第一行包含整数T(1<= T<=10000),表示测试用例数。
对于每个测试用例,存在一条包含整数n(2 <= n<=10^18)的一行,表示项链上的珠数。
Output
对于每个测试用例,输出一行答案,答案可能很大,请输出mod 10^9+7 之后的答案。
Sample Input
2 2 3
Sample Output
3 4
思路:给出一条项链,要求在这条项链中任取素数长度的一段中红色珠子数量大于等于蓝色珠子数量,求满足条件的项链的数量。
1.对于素数长度的子串我们只需要考虑满足最小的两个素数2,3就可以了,大于3的长度都可以分解为由2,3组成的串。
2.模拟:
令 1 表示红色珠子, 0 表示蓝色珠子。设 n 为珠子数量。
当 n=2 时有:
1) 11
此时后面可以接 1或0 都可以满足条件(任取长度为2或3的小段红珠数量不小于蓝珠数量).
2) 10
此时后面只能跟 1.
3) 01
此时后面只能跟 1.
由此可以得出当前两位珠子颜色都为 1 时 后面才可以跟0。 即存在 1 1 0。
而在任何条件下后面都可以跟 1。 即 1 0 1、0 1 1、1 1 1 都满足条件。
那么对于任意长度大于为n(n>3)的项链 可以通过观察长度为 n-1、n-2、n-3的项链 来推出第n位的珠子颜色有几种方案。
1)首先在 n-1 长度项链的基础上任何情况下接 1 都可以满足条件,因此接 1 的情况数量就是 n-1 长度的总方案数量。
2)对于接 0 的情况需要满足前两位(即n-1、n-2)都是 1 。而 n-1 是 1 的方案数量 是n-2长度的总方案数量,n-2 是 1 的方案数量是n-3长度的总方案数量。
因此接 0 的情况数量就是 n-3 长度的总方案数量。
3)n长度的总方案数量 = 接1的情况数量 + 接0的情况数量 = n-1长度的方案数量+n-3长度的方案数量.
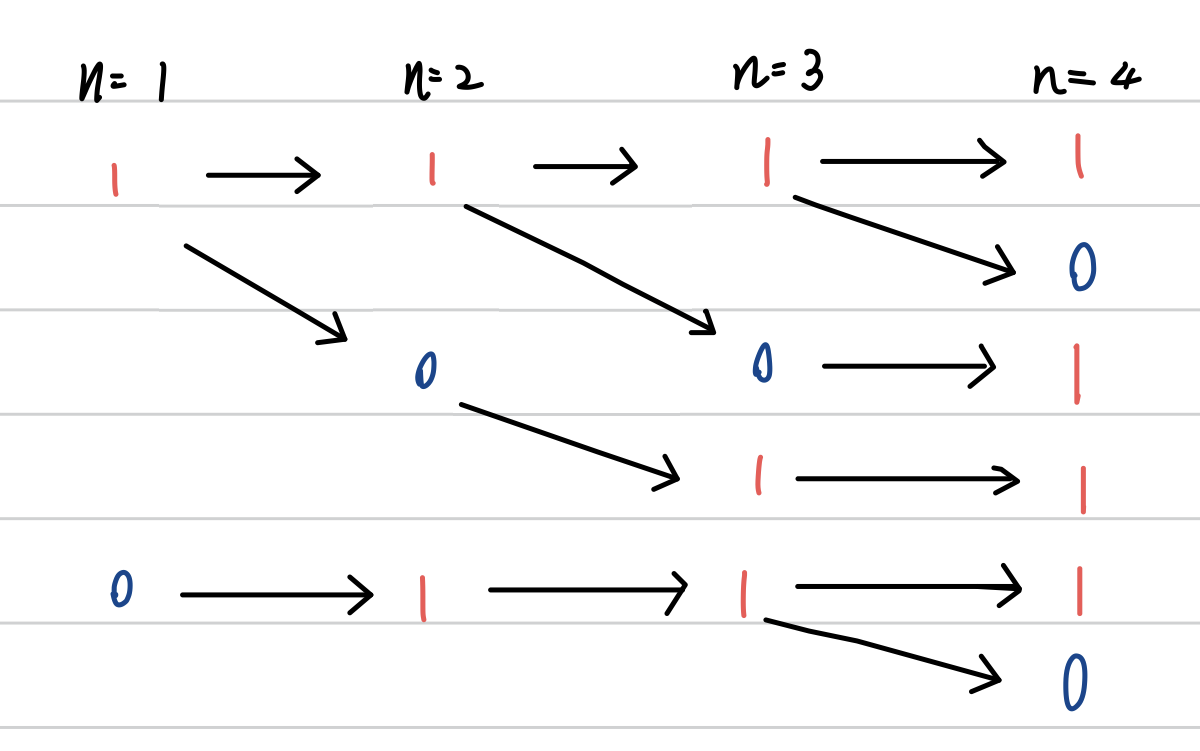
令 F(n) 表示长度为n的项链的方案数量。
3.推得公式 F(n)=F(n-1)+F(n-3)
类似斐波那契数列
构造矩阵满足
F(n)=F(n-1)+F(n-3)
F(n-1)=F(n-1)
F(n-2)=F(n-2)
AC代码:
1 #include <set> 2 #include <map> 3 #include <list> 4 #include <stack> 5 #include <queue> 6 #include <deque> 7 #include <cmath> 8 #include <string> 9 #include <vector> 10 #include <cstdio> 11 #include <cstring> 12 #include <cstdlib> 13 #include <sstream> 14 #include <iostream> 15 #include <algorithm> 16 #include <unordered_map> 17 #define INF 0x3f3f3f3f 18 #define ll long long 19 #define ull unsigned long long 20 #define fcio ios::sync_with_stdio(false); cin.tie(0); cout.tie(0) 21 using namespace std; 22 const int maxn=3; 23 const int mod=1e9+7; 24 25 struct Matrix 26 { 27 ll m[maxn][maxn]; 28 Matrix() {memset(m,0,sizeof m);} 29 }; 30 31 Matrix Multi(Matrix a,Matrix b) 32 { 33 Matrix res; 34 for(int i=0;i<maxn;i++) 35 { 36 for(int j=0;j<maxn;j++) 37 { 38 for(int k=0;k<maxn;k++) 39 { 40 res.m[i][j]=(res.m[i][j]%mod+a.m[i][k]%mod*b.m[k][j]%mod)%mod; 41 } 42 } 43 } 44 return res; 45 } 46 47 Matrix fastm(Matrix a,ll n) 48 { 49 if(n==1) return a; 50 Matrix temp=fastm(a,n/2); 51 if(n%2) return Multi(Multi(temp,temp),a); 52 else return Multi(temp,temp); 53 } 54 55 int main() 56 { 57 int t; 58 ll n; 59 fcio; 60 cin>>t; 61 while(t--) 62 { 63 cin>>n; 64 if(n<=3) 65 { 66 if(n==1) cout<<1<<endl; 67 else 68 cout<<n+1<<endl; 69 } 70 else 71 { 72 Matrix res; 73 res.m[0][0]=1; 74 res.m[0][1]=0; 75 res.m[0][2]=1; 76 res.m[1][0]=1; 77 res.m[1][1]=0; 78 res.m[1][2]=0; 79 res.m[2][0]=0; 80 res.m[2][1]=1; 81 res.m[2][2]=0; 82 res=fastm(res,n-3); 83 cout<<(4*res.m[0][0]%mod+3*res.m[0][1]%mod+2*res.m[0][2]%mod)%mod<<endl; 84 } 85 } 86 }
