(一)递归程序设计方法的要点
1) 对于含有递归特征的问题,最好设计递归形式的算法。但也不要单纯追求形式。应在算法设计的分析过程中“就事论事”。例如,在利用分割求解设计算法时,子问题和原问题的性质相同;或者,问题的当前一步解决之后,余下的问题和原问题性质相同,则自然导致递归求解。
2) 实现递归函数,目前必须利用“栈”。一个递归函数必定能改写为利用栈实现的非递归函数,反之,一个利用栈实现的非递归函数可以改写为递归函数。需要注意的是递归函数递归层次的深度决定所需存储量的大小。
3) 分析递归算法的工具是递归树,从递归树上可以得到递归函数的各种相关信息。例如:递归树的深度即为递归函数的递归深度;递归树上的结点数目恰为函数中的主要操作重复进行的次数;若递归树蜕化为单支树或者递归树中含有很多相同的结点,则表该递归函数不适用。
4) 递归函数中的尾递归都是可以容易消除的。
5) 递归函数一定要有一个递归出口。即整个递归函数应该是收敛的。规模应该越来越小。
(示例分析一)斐波那契数列
有如下的数列:1、1、2、3、5、8、13、21、34、…(n>=1)
得到如下的递推关系式:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n>=2,n∈N*)
F(2)=F(1)+F(0)=1+0=1
F(3)=F(2)+F(1)=1+1=2
F(4)=F(3)+F(2)=2+1=3
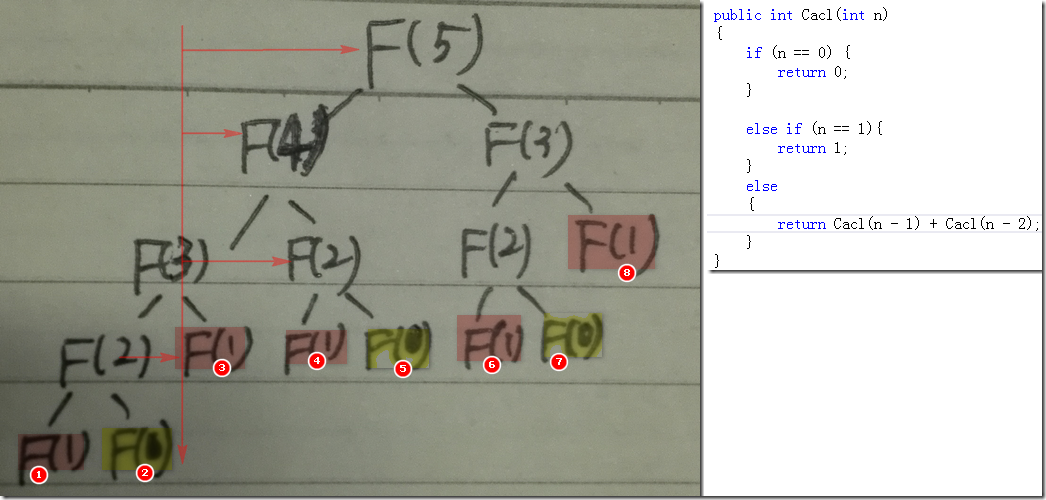
F(5)的递归树如下