给你一个包含20亿个int类型整数的文件,计算机的内存只有2GB,怎么给它们排序?一个int数占4个字节,20个亿需要80亿字节,大概占用8GB的内存,而计算机只有2GB的内存,数据都装不下!可以把8GB分割成4个2GB的数据来排,然后在把他们拼凑回去。如下图:
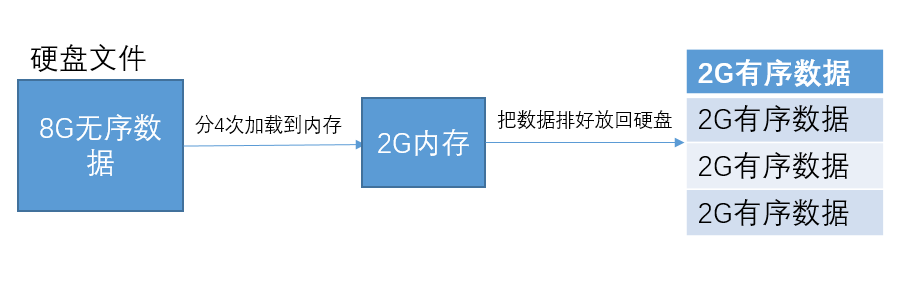
排序的时候我们可以选择快速排序或归并排序等算法。为了方便,我们把排序好的2G有序数据称之为有序子串吧。接着我们可以把两个小的有序子串合并成一个大的有序子串。

注意:读取的时候是每次读取一个int数,通过比较之后在输出。
按照这个方法来回合并,总共经过三次合并之后就可以得到8G的有序子串。
下面是一个具体事例:一共有12个无序数据,但是内存只能装下3个int数据

接下来把12个数据分成4份,然后排序成有序子串
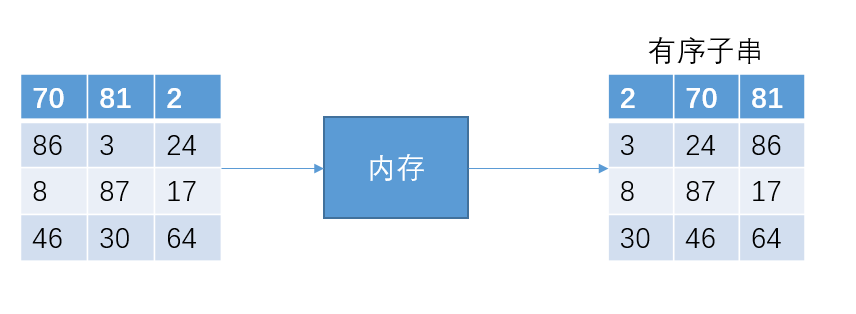
然后把子串进行两两合并
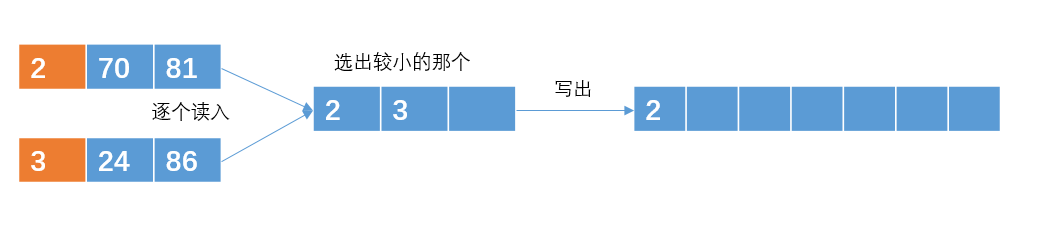
输出哪个元素,就在那个元素所在的有序子串再次读入一个元素
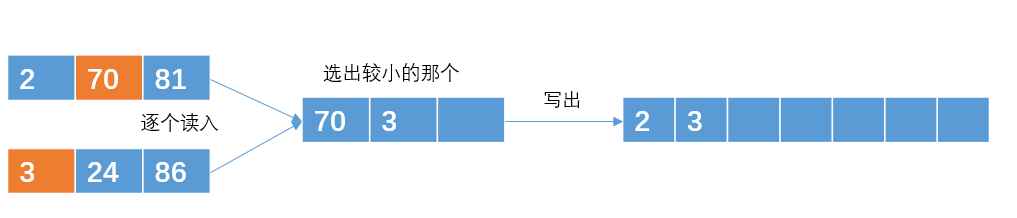
继续
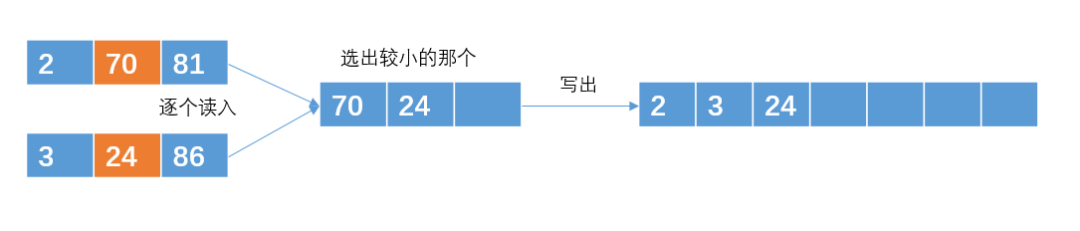
重复直到合并成一个包含6个int的有序子串

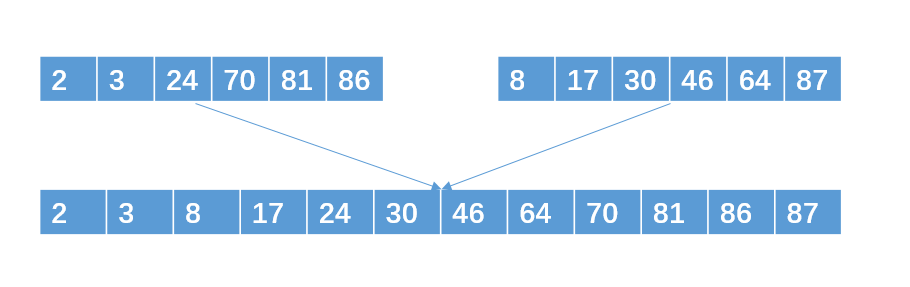
再把两个包含6个int的有序子串合并成一个包含12个int数据的最终有序子串
优化策略
因为硬盘的读写速度比内存要慢的多,按照以上这种方法,每个数据都从硬盘读了三次,写了三次,要花很多时间。
解释下:例如对于数据2,我们把无序的12个数据分成有序的4个子串需要读写各一次,把2份3个有序子串合并成6个有序子串读写各一次;把2份6个有序子串合并从12个有序子串读写各一次,一共需要读写各3次。
在进行有序子串合并的时候,不采取两两合并的方法,而是可以3个子串,或4个子串一起来合并。
多路归并
为了方便讲解,我们假设内存一共可以装4个int型数据。
刚才我们是采取两两合并的方式,现在我们可以采取4个有序子串一起合并的方式,这样的话,每个数据从硬盘读写的次数各需要2次就可以了。如图:
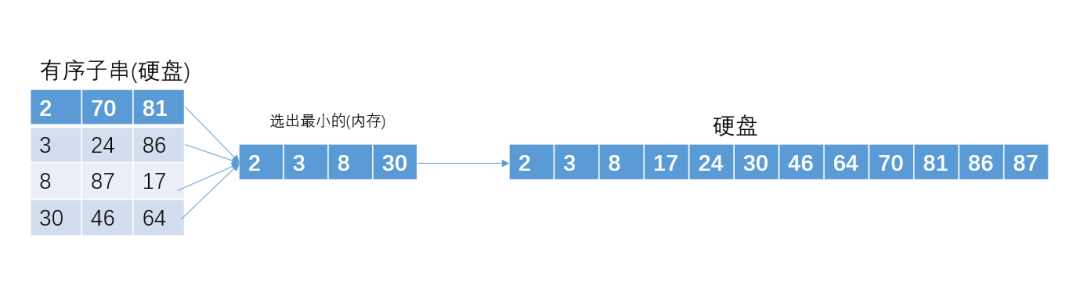
4个有序子串的合并,叫4路归并。如果是n个有序子串的合并,就把它称为n路归并。n并非越大越好。因为n越大的确可以减少磁盘IO次数,但是相应的合并期间在内存中选取最小值的时间也会相应增加
置换选择
n不是越大越好,那么我们可以想办法减少有序子串的总个数。这样,也能减少数据从硬盘读写的次数。
以前面的12个无序数据为例:

例如我们可以从12个数据读取3个存到内存中,然后从内存中选出最小的那个数放进子串p1里;之后再从剩余的9个数据读取一个放到内存中,然后再从内存中选出一个数放进子串p1里,这个数必须满足比 p1中的其他数大,且在内存中尽量小。这样一直重复,直到内存中的数都比p1中的数小,这时p1子串存放结束,继续来p2子串的存放,例如(这时假设内存只能存放3个int型数据):
读入3个到内存中,且选出一个最小的到子串p1:

从内存中再次读取一个元素86:


从内存中再次读取一个元素24:

从内存中再次读取一个元素8:

这个时候已经没有符合要求的数了,且内存已满,进而用p2子串来存放,以此类推。
通过这种方法,p1子串存放了4个数据,而原来的那种方法p1子串只能存放3个数据。
利用堆排序优化查找速度
从12个数据中读取3个数据,构建成一个最小堆,然后从堆顶选择一个数写入到p1中。
之后再从剩余的9个数中读取一个数,如果这个数比刚才那个写入到p1中的数大,则把这个数插入到最小堆中,重新调整最小堆结构,然后在堆顶选一个数写入到p1中。
否则,把这个数暂放在一边,暂时不处理。之后一样需要调整堆结构,从堆顶选择一个数写入到p1中。
这里说明一下,那被放在一边的数是不能再放入p1中的了,因为它一定比p1中的数都要小,所以它会放在下一个子串中
看这些文字会让人头大,我画图解释下吧。
从12数据读取3个数据

构建最小堆,且选出目标数
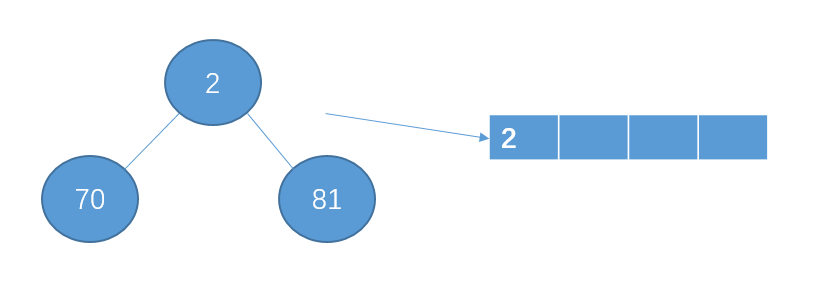
读入下一个数86
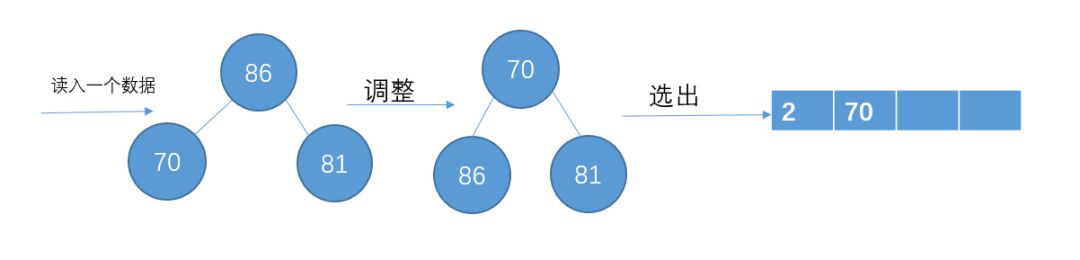
读入下一个数3,比70小,暂放一边,不加入堆结构中
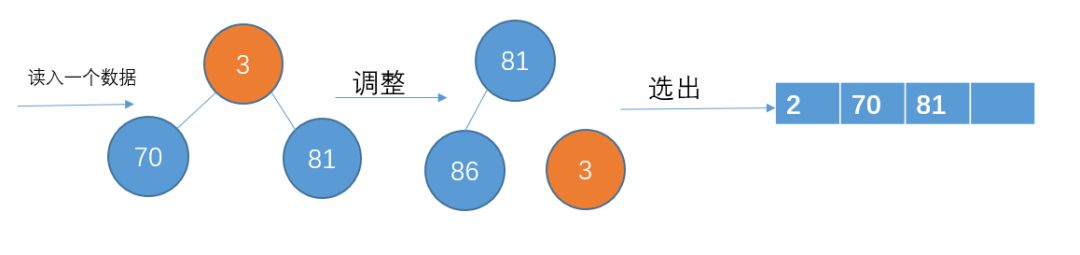
读入下一个数据24,比81小,不加入堆结构
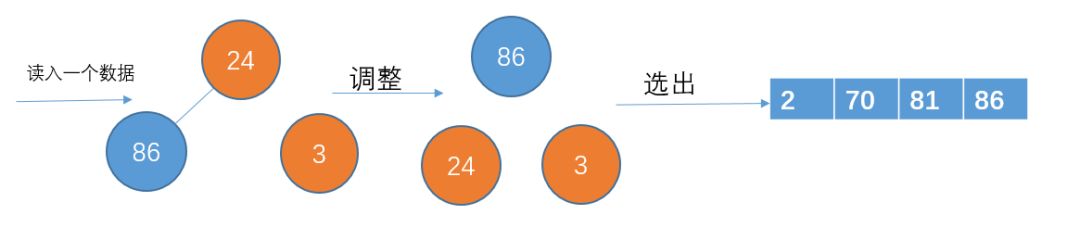
读入下一个数据8,比86小,不加入堆结构。此时p1已经完成了,把那些刚才暂放一边的数重新构成一个堆,继续p2的存放。
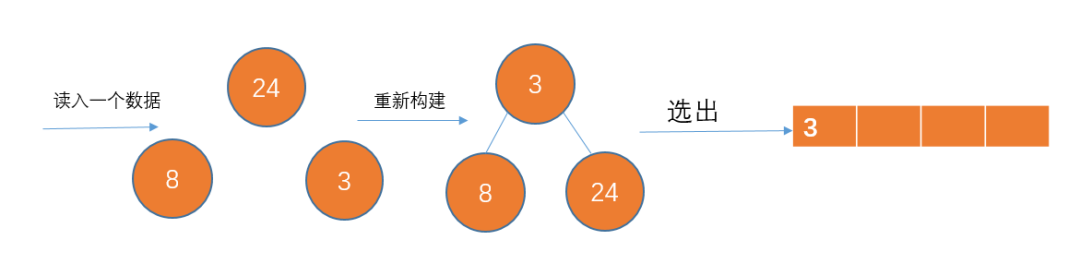
以此类推…
最后生成的p2如下:
这样子的话,最后只生成了2个有序子串,我们把这种方法称之为置换选择。按照这种方法,最好的情况下,所有数据只生成一个有序子串;最坏的情况下,和原来没采取置换选择算法一样,还是4个子串,那平均性能如何呢?
结论:如果内存可以容纳n个元素的话,那么平均每个子串的长度为2n,也就是说,使用置换选择算法我们可以减少一半的子串数。
这种方法适合要排序的数据太多,以至于内存一次性装载不下。只能通过把数据分几次的方式来排序,把这种方法称为外部排序。