物理选修3-1 电场,电场强度和电场线

• 电场

电荷的周围存在电场,场是物质的一种存在形式

• 电场强度

1. 检验电荷

用来检验电场是否存在及其强弱分布情况的电荷,特点是体积小,电荷量小,不会对研究造成任何影响

1. 场源电荷

被检验的电场是由电荷Q所激发的,则电荷Q称为场源电荷

1. 电场强度

比值定义:$E=frac{F}{q}$,单位$V$/$m$($N$/$C$)

方向:为该点正电荷受到的电场力方向

点电荷的电场强度:$E=frac{F}{q}=frac{frac{kQq}{r^2}}{q}=frac{kQ}{r^2}$

电场强度的叠加:根据电场强度的矢量性,电场强度可以根据平行四边形法则进行叠加

均匀带电体(或球壳)外某点电场强度的计算:可以用公式$frac{kQ}{r^2}$,r是球心到该点的距离,Q为整个球体的带电量(这个比较神奇,深层次原理我也不知道..)

• 电场力

由电场强度的定义式可以导出电场力的公式之一:$F=Eq$

• 电场线

法拉第首先引入电场线这个概念来描述电场的性质

电场线的性质:

1. 曲线上任意一点的切线方向和其场强方向一致

2. 电场强度较大的地方电场线密集,较小的地方电场线稀疏

3. 电场线并不实际存在,且分布于整个立体空间内

常见的电场线:

1. 单个正电荷为场源电荷:电场线发散状

2. 单个负电荷为场源电荷:电场线汇聚状

3. 两个等电量同种电荷为场源电荷:电场线相斥状

4. 两个等电量异种电荷为场源电荷:电场线相吸状

5. 匀强电场平行线状

   • 匀强电场

各个点的电场强度相等的电场叫做匀强电场

特点:

1. 电场强度方向处处相同且大小处处相等,所以电场线是等距平行线

2. 带电粒子在匀强电场里受到恒定的电场力作用

题型总结

求解电场强度

直接求解

对于点电荷,$E=frac{F}{q}$和$E=frac{kQ}{r^2}$都是可以使用的

对于任意电荷,只能够用定义式,即$E=frac{F}{q}$

利用场的叠加原理

这种方法的使用特征是:当带电体不能够看做点电荷的时候,核心思想就是使用微元法来解决不能够看做点电荷的问题,比如:

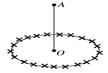
如图所示，一个均匀的带电圆环，带电荷量为＋Q，半径为R，放在绝缘水平桌面上．圆心为O点，过O点作一竖直线，在此线上取一点A，使A到O点的距离为R，在A点放一检验电荷＋q，则＋q在A点所受的电场力为?

解:

取环上长度为$triangle x$的一段,则其带电量为$triangle Q=Qtimes frac{triangle x}{2pi R}$,对A的库仑力为$F=frac{ktriangle Q q}{(sqrt {2}R)^2}=Qtimes frac{triangle x}{2pi R}times frac{k q}{(sqrt {2}R)^2}=frac{Qtriangle xkq}{4pi R^3}$

接下来考虑所有的长度为$triangle x$的一段对A的影响:根据对称性,水平方向上的分力抵消;竖直方向上:

$F_y=sum F_icosfrac{pi}{4}=frac{2pi R}{triangle x}times Fcosfrac{pi}{4}=frac{2pi R}{triangle x}times frac{Qtriangle xkq}{4pi R^3}times frac{sqrt2}{2}=frac{sqrt 2kQq}{4R^2}$

因此大小为$frac{sqrt 2kQq}{4R^2}$,方向竖直向上

利用对称法求解

这种方法的特征特别明显:电荷的分布具有对称性的时候(书上说的)

具体做法是:巧妙而合适的假设放置额外电荷,或将电荷巧妙的分割,是问题简化而求的未知的电场强度(也是书上说的哈哈)

例题:

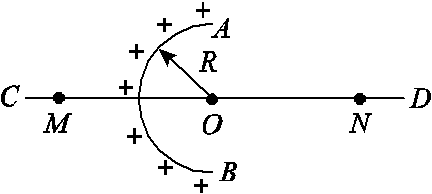
均匀带电的球壳在球外空间产生的电场等效于电荷集中于球心处产生的电场.如图所示，在半球面AB上均匀分布正电荷，总电荷量为q,球面半径为r,CD 为通过半球顶点与球心 O 的轴线，在轴线上有 M ,N 两点,OM＝ON=2r.已知 M 点的场强大 大专栏  物理选修3-1 电场,电场强度和电场线小为 E,则 N 点的场强大小为?

解:

一个完整球壳对N点的场强大小为$E=frac{2kq}{(2r)^2}=frac{kq}{2r^2}$

而半个球壳对M的场强大小为E,也就是对N点的场强大小为E,且两个球壳在电场上等价,因此半个球壳对N的场强大小为$frac{kq}{2r^2}-E$

利用电场强度和电势差的关系求解

留坑待补(可能我不会补了吧~~)

电场线

由电场线和运动轨迹判断带电粒子的运动情况

这种题型需要注意两点

• 做曲线运动的粒子所受合外力方向指向曲线凹侧

• 粒子的速度沿着轨迹的切线方向

两个等量电荷电场

分类讨论可得,两个等量电荷电场有两种情况:两个同种电荷,两个异种电荷(以下简称等量同种,等量异种)

这个东西需要掌握点的主要为:

• 场强的极值

• 中垂线(面)上场强的变化规律

等量异种

• 电场极值

电场在连线中点上场强最小,越靠近点电荷场强越强,可以证明以下(不知道这种证法算不算伪证):

设两端点电荷电荷量的绝对值为Q,连线上任意一点电荷量为q(假设是正电荷,负电荷为这种情况的对称情况,不消讨论),q和左边的电荷相距$l_1$,和右边的电荷相距$l_2$;

则q的场强为$E=frac{kqQ}{l_1^2}+frac{kqQ}{l_2^2}=kqQ(frac{1}{l_1^2}+frac{1}{l_2^2})$

根据基本不等式,$frac{1}{l_1^2}+frac{1}{l_2^2}>=2sqrt{frac{1}{l_1^2l_2^2}}=frac{2}{l_1l_2}$,当且仅当$l_1=l_2$的时候有最小值$frac{2}{l_1l_2}$

得证.

• 中垂线(面)上场强的变化规律

在中垂线(面)上场强方向不变,场强大小在O点最大,且向两边对称递减

等量同种

• 电场极值

O点无电场外,其他点都有电场

中垂线上的最大场强比较神奇:

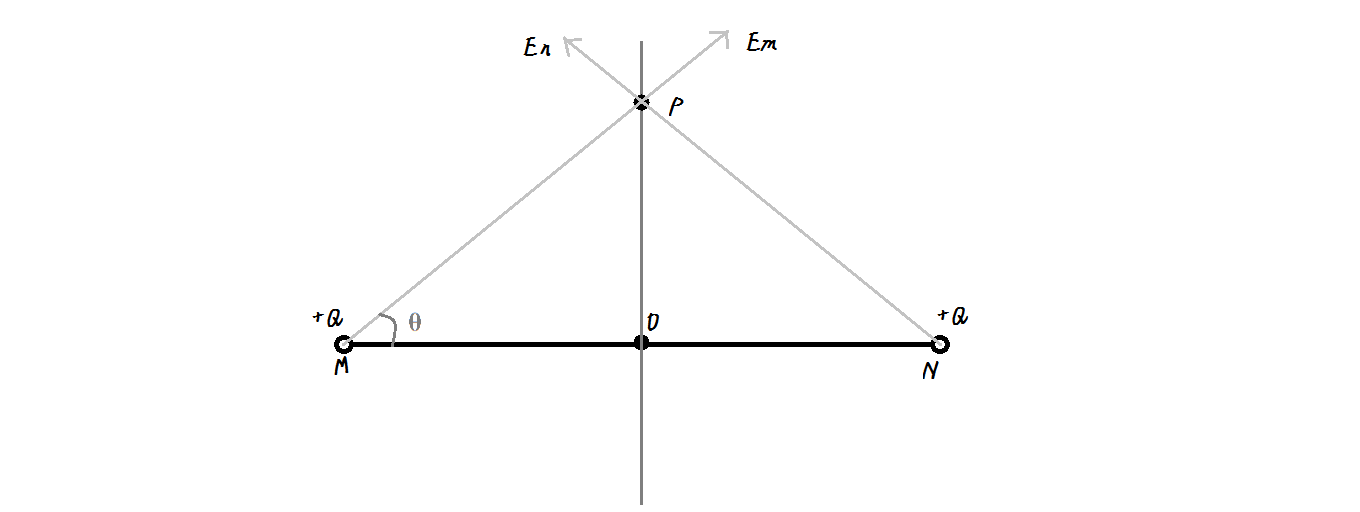
设MN=2L

于是$E_m=E_n=frac{kQ}{(frac{L}{costheta})^2}$,P点的合场强$E_p=2E_msintheta=frac{2kQcos^2theta sintheta}{L^2}$

当$2cos^2theta sintheta$最大的时候$E_p$最大

这时有一个神奇的不等式:$abc<=(frac{a+b+c}{3})^3$(暂时还没有想到怎么去证明这个不等式)

code

update 2019年10月24日10:04:35

今天在听微积分课的时候听到了这个不等式,其实它叫做平均值不等式,用自然语言描述就是算术平均值不小于其几何平均值,即

但还是没有讲到怎么证明这个不等式…..

因此$2(cos^2theta sintheta)=(1-sin^2theta)(1-sin^2theta)2sin^2theta<=(frac{2}{3})^3$

当$1-sin^2theta=2sin^2theta$,也就是$sintheta=frac{sqrt3}{3}$时$E_p$最大,等于$frac{4sqrt3 kQ}{9L^2}$

• 中垂线(面)上场强的变化规律

场强方向总沿面(线)远离O(等量正电荷)或指向O(等量负电荷),且从O点到无穷远,电场线先变密后变疏,场强先变强后变弱

叠加场

这个方法的意思就是利用等效原理将多个场的问题转化为一个场的问题.一般来讲就是把电场和重力场转化为一个等效重力场(记得我上个学期听到过这种方法,当时叫的是等效重力法)

使用的特征就是当场的力的形式不发生改变的时候,说白了就是场力方向不随位置改变而改变,对应到电场里面就是匀强电场了

例题就懒得给了