[bzoj4823][洛谷P3756][Cqoi2017]老C的方块

Description###

老 C 是个程序员。
作为一个懒惰的程序员,老 C 经常在电脑上玩方块游戏消磨时间。游戏被限定在一个由小方格排成的R行C列网格上
,如果两个小方格有公共的边,就称它们是相邻的,而且有些相邻的小方格之间的公共边比较特殊。特殊的公共边排
列得有很强的规律。首先规定,第1行的前两个小方格之间的边是特殊边。然后,特殊边在水平方向上每4个小方格为
一个周期,在竖直方向上每2个小方格为一个周期。所有的奇数列与下一列之间都有特殊边,且所在行的编号从左到
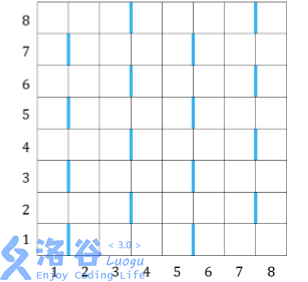
右奇偶交替。下图所示是一个R = C = 8的网格,蓝色标注的边是特殊边。首先,在第1行,第1列和第2列之间有一条
特殊边。因为竖直方向周期为2,所以所有的奇数行,第1列和第2列之间都有特殊边。因为水平方向周期为4,所以所
有奇数行的第5列和第6列之间也有特殊边,如果网格足够大,所有奇数行的第9列和第10列、第13列和第14列之间都
有特殊边。因为所有的奇数列和下一列之间都有特殊边,所以第3列和第4列、第7列和第8列之间也有特殊边,而所在
行的编号从左到右奇偶交替,所以它们的特殊边在偶数行。如果网格的规模更大,我们可以用同样的方法找出所有的
特殊边。

网格的每个小方格刚好可以放入一个小方块,在游戏的一开始,有些小方格已经放上了小方块,另外的小方格没有放
。老 C 很讨厌下图所示的图形,如果他发现有一些小方块排列成了它讨厌的形状(特殊边的位置也要如图中所示),
就很容易弃疗,即使是经过任意次旋转、翻转后排列成讨厌的形状,老 C 也同样容易弃疗。

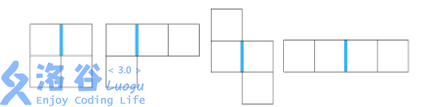
为了防止弃疗,老 C 决定趁自己还没有弃疗,赶紧移除一些格子里小方块,使得剩下的小方块不能构成它讨厌的形状
。但是游戏里每移除一个方块都是要花费一些金币的,每个方块需要花费的金币有多有少参差不齐。老 C 当然希望
尽可能少的使用游戏里的金币,但是最少要花费多少金币呢?老 C 懒得思考,就把这个问题交给你了

Input###

第一行有3个正整数C, R, n,表示C列R行的网格中,有n个小方格放了小方块。
接下来n行,每行3个正整数x, y, w,表示在第x列第y行的小方格里放了小方块,移除它需要花费w个金币。保证不会
重复,且都在网格范围内。
1 ≤ C, R, n ≤ 10^5 , 1 ≤ w ≤ 10^4

Output###

输出一行,包含一个整数,表示最少花费的金币数量。

Sample Input###

2 2 4

1 1 5

1 2 6

2 1 7

2 2 8

Sample Output###

5

---

简要题解##

染色分层+最小割

---

想法##

观察使老C弃疗的图形

发现它们都由特殊边两边的紫色格子，及一个蓝格子、一个绿格子组成。

由此我们可以给整张图染色

（为了方便我把两个紫格子分别染成紫与深蓝）

我们需要移除一些格子使图中不存在连续的 蓝-紫-深蓝-绿 或 绿-紫-深蓝-蓝
由此可以想到用最小割（有一句话说得好：灵感源于性质的相似性）
最小割即把对点的限制转换到对边的限制上。

开始建图。
S向每个绿格子连边，容量为绿格子的w
每个绿格子向相邻的紫格子与深蓝格子连边，容量为INF
紫格子与相邻深蓝格子互相连边，容量为两个格子w的min （其实这两个相邻的点是一体的，就相当于是一个大点。这两个点中间连边相当于拆大点。）
紫格子与深蓝格子向相邻的蓝格子连边，容量为INF
蓝格子向T连边，容量为蓝格子的w

---

代码##

这道题A的真是不容易……
一开始懒得写hash表光写个hash，结果那么不幸就被卡上了……
（哎，这是第二次了……之前有一次cf没写hash表被hack了…）
调了好久好久，不开森。

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<vector>

#define INF 2000000007
#define P 100999

using namespace std;

typedef long long ll;
const int N = 100007;

struct node{
    int v,f;
    node *next,*rev;
}pool[N*10],*h[N];
int cnt;

void addedge(int u,int v,int f){
    node *p=&pool[++cnt],*q=&pool[++cnt];
    p->v=v;p->next=h[u];h[u]=p; p->f=f;p->rev=q;
    q->v=u;q->next=h[v];h[v]=q; q->f=0;q->rev=p;     
}

int S,T;
int que[N],level[N];
bool bfs(){
    int head=0,tail=0,u,v;
    for(int i=S;i<=T;i++) level[i]=-1;
    level[S]=1; que[tail++]=S;
    while(head<tail){
        u=que[head++];
        for(node *p=h[u];p;p=p->next)
            if(p->f && level[v=p->v]==-1){
                level[v]=level[u]+1;
                que[tail++]=v;   
            }
        if(level[T]!=-1) return true;
    } 
    return false;
}
int find(int u,int f){
    int v,s=0,t;
    if(u==T) return f;
    for(node *p=h[u];p;p=p->next)
        if(p->f && s<f && level[v=p->v]==level[u]+1){
            t=find(v,min(p->f,f-s));
            if(t){
                s+=t;
                p->f-=t;
                p->rev->f+=t;
            }
        }
    if(!s) level[u]=-1;
    return s;
}
int dinic(){
    int flow=0;
    while(bfs()) flow+=find(S,INF);
    return flow;    
}

int C,R,n;

struct data{
    int x,y,w,id;  
}d[N];

int hash(int x,int y) { 
    if(x<=0 || y<=0 || x>R || y>C) return P;
    return ((ll)x*N+y)%P; 
}
vector<data> hh[P+1];

int check(int c,int x,int y){
    if(c==P) return 0;
    for(int i=0;i<hh[c].size();i++)
        if(hh[c][i].x==x && hh[c][i].y==y) return hh[c][i].id;
    return 0;
}

int main()
{
    scanf("%d%d%d",&C,&R,&n);
    for(int i=1;i<=n;i++){
        scanf("%d%d%d",&d[i].y,&d[i].x,&d[i].w);
        d[i].id=i;
        hh[hash(d[i].x,d[i].y)].push_back(d[i]);
    }
    
    //addedge
    int t,xx,yy;
    S=0; T=n+1;
    for(int i=1;i<=n;i++){
        xx=d[i].x%2; yy=d[i].y%4;
        if((xx==1 && yy==1) || (xx==0 && yy==3)){ //purple
            t=check(hash(d[i].x,d[i].y+1),d[i].x,d[i].y+1);
            if(t) addedge(i,t,min(d[i].w,d[t].w));
        }
        else if((xx==1 && yy==2) || (xx==0 && yy==0)){ //dark blue
            t=check(hash(d[i].x,d[i].y-1),d[i].x,d[i].y-1);
            if(t) addedge(i,t,min(d[i].w,d[t].w)); 
        }
        else if((xx==1 && yy==3) || (xx==0 && yy==2)){ //green
            addedge(S,i,d[i].w);
            t=check(hash(d[i].x+1,d[i].y),d[i].x+1,d[i].y);
            if(t) addedge(i,t,INF);
            t=check(hash(d[i].x-1,d[i].y),d[i].x-1,d[i].y);
            if(t) addedge(i,t,INF);
            if(yy==3) 
                t=check(hash(d[i].x,d[i].y-1),d[i].x,d[i].y-1);
            else t=check(hash(d[i].x,d[i].y+1),d[i].x,d[i].y+1);
            if(t) addedge(i,t,INF); 
        }
        else{ //blue
            addedge(i,T,d[i].w);
            t=check(hash(d[i].x+1,d[i].y),d[i].x+1,d[i].y);
            if(t) addedge(t,i,INF);
            t=check(hash(d[i].x-1,d[i].y),d[i].x-1,d[i].y);
            if(t) addedge(t,i,INF);
            if(yy==1) 
                t=check(hash(d[i].x,d[i].y-1),d[i].x,d[i].y-1);
            else t=check(hash(d[i].x,d[i].y+1),d[i].x,d[i].y+1);
            if(t) addedge(t,i,INF); 
        }
    }
    
    printf("%d
",dinic());
    
    return 0;
}