luogu_P2051 [AHOI2009]中国象棋

https://www.luogu.org/problem/P2051

题目描述

这次小可可想解决的难题和中国象棋有关，在一个N行M列的棋盘上，让你放若干个炮（可以是0个），使得没有一个炮可以攻击到另一个炮，请问有多少种放置方法。大家肯定很清楚，在中国象棋中炮的行走方式是：一个炮攻击到另一个炮，当且仅当它们在同一行或同一列中，且它们之间恰好 有一个棋子。你也来和小可可一起锻炼一下思维吧！

输入格式

一行包含两个整数N，M，之间由一个空格隔开。

输出格式

总共的方案数，由于该值可能很大，只需给出方案数模9999973的结果。

输入输出样例

输入 #1复制

1 3

输出 #1复制

7

说明/提示

样例说明

除了3个格子里都塞满了炮以外，其它方案都是可行的，所以一共有2*2*2-1=7种方案。

数据范围

100%的数据中N和M均不超过100

50%的数据中N和M至少有一个数不超过8

30%的数据中N和M均不超过6

---

转自：https://www.luogu.org/blog/RPdreamer/p2051，有修改

设出状态：

f[i][j][k]代表放了前i行,有j列是有一个棋子,有k列是有2个棋子的合法方案数.

（状态难想，但转移方程就比较明显）

转移：

一.第i行不放棋子

我们可以直接继承上面的状态.即f[i][j][k]=f[i-1][j][k]

二.第i行放一个棋子

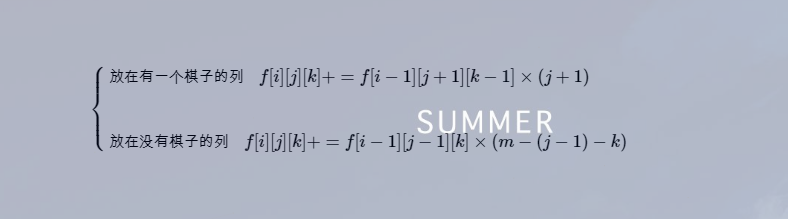
三.第i行放两个棋子

#include<iostream>
#include<cstdio>

#define ri register int
#define u long long

namespace opt {

    inline u in() {
        u x(0),f(1);
        char s(getchar());
        while(s<'0'||s>'9') {
            if(s=='-') f=-1;
            s=getchar();
        }
        while(s>='0'&&s<='9') {
            x=(x<<1)+(x<<3)+s-'0';
            s=getchar();
        }
        return x*f;
    }

}

using opt::in;

#define MO 9999973
#define NN 105

namespace mainstay {

    u N,M,f[NN][NN][NN];
    
    inline u c_(const u &x){
        return (x*(x-1)/2)%MO;
    }

    inline void solve() {
        N=(in()),M=(in());
        f[0][0][0]=1;
        u m(M);
        for(ri i(1); i<=N; ++i) {
            for(ri j(0); j<=M; ++j) {
                for(ri k(0); k<=M; ++k) {
                    if(j+k>M) continue;
                    //不放 ： 
                    f[i][j][k]=(f[i][j][k]+f[i-1][j][k])%MO;
                    //在空白列放一个： 
                    if(j-1>=0) f[i][j][k]=(f[i][j][k]+f[i-1][j-1][k]*(M-k-j+1))%MO;
                    // 在一个棋子列上放一个 
                    if(k-1>=0) f[i][j][k]=(f[i][j][k]+f[i-1][j+1][k-1]*(j+1))%MO;
                    //在空白列放两个 
                    if(j-2>=0) f[i][j][k]=(f[i][j][k]+f[i-1][j-2][k]*c_(m-j-k+2))%MO;
                    //在一个棋子列上放一个 ，并且在空白列放一个 
                    if(k-1>=0) f[i][j][k]=(f[i][j][k]+f[i-1][j][k-1]*(M-j-k+1)*(j))%MO;
                    //在一个棋子列上放两个 
                    if(k-2>=0) f[i][j][k]=(f[i][j][k]+f[i-1][j+2][k-2]*c_(j+2))%MO;
                }
            }
        }
        u ans(0);
        for(ri i(0);i<=M;++i){
            for(ri j(0);j<=M;++j){
                if(i+j<=M) ans=(ans+f[N][i][j])%MO;
            }
        }
        std::cout<<ans;
    }

}

int main() {

    //freopen("T2.in","r",stdin);
    //freopen("T2.out","w",stdout);
    std::ios::sync_with_stdio(false);
    mainstay::solve();

}