之前几个排序时间复杂度是n方,接下来这几个速度就要比较快了
ShellSort.h
1 #pragma once 2 #include "swap.h" 3 #include <vector> 4 using namespace std; 5 template <class T> 6 void ShellSort(vector<T> &v) { 7 int increment = v.size(), j; 8 do 9 { 10 increment = increment / 3 + 1; 11 for (auto i = increment; i < v.size(); i++) 12 { 13 if (v[i] < v[i - increment]) 14 { 15 T tmp = v[i]; 16 j = i; 17 for (; j - increment >= 0 && tmp < v[j - increment]; j -= increment) 18 { 19 v[j] = v[j - increment]; 20 } 21 v[j] = tmp; 22 } 23 } 24 } while (increment > 1); 25 26 }
希尔排序
它的做法是:
将间隔的元素看作一个子序列,对其进行插入排序
缩小间隔,继续对子序列排序
直到间隔为1
比如10个元素
将147 10,258,369分别插入排序
然后对13579,2468 10分别插入排序
最后整体插入排序
HeapSort.h
1 #pragma once 2 #include "swap.h" 3 #include <vector> 4 using namespace std; 5 template <class T> 6 void HeapAdjust(vector<T> &v, int s, int m) { 7 T tmp; 8 tmp = v[s]; 9 for (auto i = 2 * (s + 1) - 1; i < m; i = (i + 1) * 2 - 1) 10 { 11 if (i < m - 1 && v[i] < v[i + 1]) 12 i++; 13 if (tmp >=v[i]) 14 break; 15 v[s] = v[i]; 16 s = i; 17 } 18 v[s] = tmp; 19 } 20 21 template <class T> 22 void HeapSort(vector<T> &v) { 23 for (int i = v.size() / 2 - 1; i >= 0; i--) 24 HeapAdjust(v, i, v.size()); 25 for (int i = v.size() - 1; i > 0; i--) 26 { 27 swapLHW(v, 0, i); 28 HeapAdjust(v, 0, i); 29 } 30 }
堆排序
将数据看成一个堆
堆是具有下列性质的完全二叉树:
每个节点的值都大于等于其左右孩子的节点,且右孩子大于等于左孩子,叫做大顶堆
每个节点的值都小于等于其左右孩子的节点,且右孩子小于等于左孩子,叫做小顶堆
我们这里用大顶堆
总体思想是,
1. 先用HeapAdjust函数将数据修改为大顶堆
2. 然后把第一个(最大的一个)与最后一个互换
3. 排除最后一个,重新进行1步骤,直到只剩一个元素为止
HeapAdjust函数的流程为
假设输入的序列s到m中,除了s以为其他都复合大顶堆
则调整s与子树的位置,使s也符合大顶堆
1. 将s与其左右孩子对比,找到最大的那个
2. 比较如果s小于孩子,则继续找孩子的孩子,直到s大于某个节点的孩子
3.s与该节点换位
MergingSort.h
1 #pragma once 2 #include "swap.h" 3 #include <vector> 4 using namespace std; 5 template <class T> 6 void Merge(vector<T> &v1, vector<T> &v2, int s, int m, int t) { 7 int i = s, j = m + 1,k = s; 8 for (; i <= m && j <= t;) 9 { 10 if (v1[i] <= v1[j]) 11 v2[k++] = v1[i++]; 12 else 13 v2[k++] = v1[j++]; 14 } 15 if (i <= m) 16 for (; i <= m; i++) 17 v2[k++] = v1[i]; 18 if (j <= t) 19 for (; j <= t; j++) 20 v2[k++] = v1[j]; 21 22 } 23 24 template <class T> 25 void MSort(vector<T> &v1, vector<T> &v2, int s, int t ) { 26 int m; 27 vector<T> vTmp(v1, size); 28 if (s == t) 29 v2[s] = v1[s]; 30 else 31 { 32 m = (s + t) / 2; 33 MSort(v1, vTmp, s, m); 34 MSort(v1, vTmp, m + 1, t); 35 Merge(vTmp, v2, s, m, t); 36 } 37 } 38 39 template <class T> 40 void MergingSort(vector<T> &v) { 41 MSort(v, v, 1, v.size()); 42 } 43 44 template <class T> 45 void MergePass(vector<T> &v1, vector<T> &v2, int s, int n) { 46 int i = 0; 47 while (i <= n - 2 * s + 1) //i+2*s-1 <= n 48 { 49 Merge(v1, v2, i, i + s - 1, i + 2 * s - 1); //因为i本身算1个 50 i += 2 * s; 51 } 52 if (i < n - s + 1) //i+s-1<n 53 { 54 Merge(v1, v2, i, i + s - 1, n); 55 } 56 else 57 { 58 for (auto j = i; j <= n; j++) 59 { 60 v2[j] = v1[j]; 61 } 62 } 63 } 64 65 template <class T> 66 void MergingSort2(vector<T> &v) { 67 vector<T> Vtmp(v.size()); 68 int k = 1; 69 while (k < v.size()) 70 { 71 MergePass(v, Vtmp, k, v.size()-1); 72 k *= 2; 73 MergePass(Vtmp, v, k, v.size()-1); 74 k *= 2; 75 } 76 }
归并排序
首先是一个递归结构
Msort函数是一个递归函数
它的目的是将输入的数列(v1)的第s个到第t个进行归并排序,放入v2
流程是:
建立一个临时变量tmp
如果s和t是相同的,则将v1[s]存入v2[s]
否则将s与t的数列拆成两段(一半)递归调用Msort,将结果存入tmp
递归返回后使用merge函数将s到t这个子序列按照从小到大的顺序插入v2
所以归并排序的整体思路是
先将数列分成2个一组的子序列
将每组子序列排序
接着将2个一组的子序列合并为4个一组的子序列,并排序
一直到将整个数列合并为一组
merge函数的目的是将输入的数列中的s到m,与m+1到t两个部分合并为一个有序的部分
所以i和j依次代表遍历两个部分的变量
比较v[i]与v[j]
哪个小,推入到新序列,并将i或者j递增
直到i到达m或者j到达t
最后检查一下如果前后两段数组还有剩余,则都插入新序列后面
不过如果使用递归,空间复杂度太高
所以还提供了一个非递归的MergingSort2
只需要一个等大的临时变量tmp
设置一个子序列长度k,先为1
接着while循环,条件是k小于数组长度
然后调用MergePass函数
该函数将v中的元素按照k个为一组,将相邻的2组排序归并为一组
比如k为1,则将1,2排序归并为1组,2,3排序归并为1组……
然后k*=2
再调用MergePass
最后k*=2
一次循环结束
MergePass函数的目的是将v1中的元素按照s个为一组,每两组归并为1组,存入v2,n为数列长度
首先建立v1的下标i=0
然后是while循环,直到下标i > n - 2 * s + 1退出循环
这里需要说明一下,如果i > n - 2 * s + 1,则i+2*s-1>n,下标将越界
在条件范围内,调用merge函数,将v1中的i到i+s-1与i+s到i+2s归并然后存入v2
i += 2 * s
循环结束后,可能会剩下一些元素没有归并
那么分两种情况:
1. 如果i < n - s + 1说明i+s-1<n,也就是说剩下元素大于s个
可以再进行一次归并,只是归并的第一个部分是s个,第二个要小于s
2. 如果i >= n - s + 1说明i+s-1>=n,也就是说剩下的元素小于等于s个
不够一次归并,所以直接将剩下的元素插入v2的尾部
QuickSort.h
1 #pragma once 2 #include "swap.h" 3 #include <vector> 4 using namespace std; 5 template <class T> 6 int Partition(vector<T> &v, int low, int high) { 7 int key = v[low]; 8 while (low < high) 9 { 10 while (low < high && v[high] >= key) 11 { 12 high--; 13 } 14 swapLHW(v, low, high); 15 while (low < high && v[low] <= key) 16 { 17 low++; 18 } 19 swapLHW(v, low, high); 20 } 21 return low; 22 } 23 24 template <class T> 25 void QSort(vector<T> &v,int low, int high) { 26 int mid; 27 if (low < high) 28 { 29 mid = Partition(v, low, high); 30 QSort(v, low, mid - 1); 31 QSort(v, mid + 1, high); 32 } 33 34 } 35 36 template <class T> 37 void QuickSort(vector<T> &v) { 38 QSort(v, 0, v.size() - 1); 39 }
快速排序
也是一个递归的过程
Qsort将递归调用自身
Qsort函数的目的是将输入序列v的第low个元素放置于这个序列中low到high这个子序列中的正确的位置mid
然后递归调用low,mid和mid+1和high
所以快速排序的流程就是
将待排序的数列中第一个元素放置于他合适的位置
该元素将数列分成两部分
其左侧所有元素都小于等于它,其右侧所有元素都大于等于它
左侧部分继续将第一个元素放在正确的位置
右侧部分同样
最后将每个元素都放在了正确的位置
partition函数是将输入的序列的第low个元素放置于这个序列中low到high这个子序列中的正确的位置,并返回这个位置
具体流程是
while循环直到low不小于high
将v[low]保存在tmp中
比较v[high]的值与tmp的值,如果tmp小则将high递减,直到tmp大于v[high]
将v[high]与v[low]交换
比较v[low]的值与tmp的值,如果tmp大则将low递增,直到tmp小于v[low]
将v[high]与v[low]交换
循环后返回low
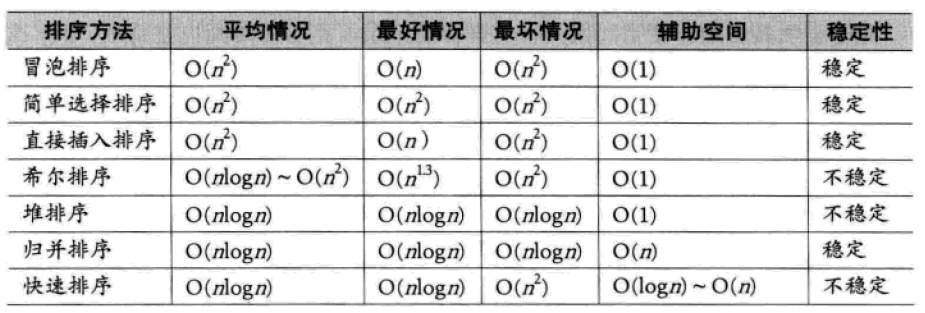
图片来源:大话数据结构,侵删