ng机器学习视频笔记(十)
——SVM进一步认识
(转载请附上本文链接——linhxx)
一、概念
svm称为支持向量,所谓的支持向量,就是在后面划分最大间距的时候,参与运算的向量,且最终新的样本进行比较,也只需要通过支持向量进行比较就可以了,不关心离边界线太远的其他向量。
下图,在一个二维环境中,其中点R,S,G点和其它靠近中间黑线的点可以看作为支持向量,它们可以决定分类器,也就是黑线的具体参数。
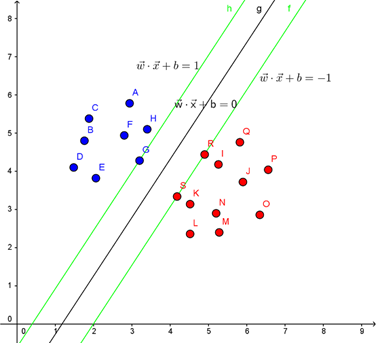
对于函数:f(x)=xwT+bf(x)=xwT+b
对于C1类的数据 xwT+b⩾1。其中至少有一个点xi,f(xi)= 1。这个点称之为最近点。
对于C2类的数据 xwT+b ⩽−1。其中至少有一个点xi,f(xi)=−1。这个点称也是最近点。
上面两个约束条件可以合并为:
yif(xi)=yi(xiwT+b)⩾1,yif(xi)=yi (xiwT+b)⩾1。yi是点xi对应的分类值(-1或者1)。因此,线性条件下,f(x)的公式为:f(x)=xwT+b;限制条件为:yif(xi)=yi (xiwT+b)⩾1,i=1,...,n
二、最大几何间隔
f(x)为函数间隔γ。γ=yf(x)/||w||,其中||w||= 。因此,问题可以转变为max 1/||w||,要求的条件是yi (xiwT+b)⩾1,i=1,...,n。可以将求max 1/||w||等价转换成球min 0.5 ||w||2。
。因此,问题可以转变为max 1/||w||,要求的条件是yi (xiwT+b)⩾1,i=1,...,n。可以将求max 1/||w||等价转换成球min 0.5 ||w||2。
现在考虑需要用拉格朗日乘子法和KKT条件来求w和b。这里要求的最优化问题是min 0.5 ||w||2,限制条件是1- yi (xiwT+b)≤0。
为了求解最大几何间隔,求出w和b,使用拉格朗日乘子法,要引入参数α,并对w和b求偏导数,令每个偏导数分别等于0。公式如下:

注意到,上图中的第二个式子,αy相乘求和为0,是L对b求偏导数,并令其为0的结果;第四个式子,关于w的式子,是L对w求偏导数,并令其为0的结果。
把上面的w的结果,带入其他的式子,得到:
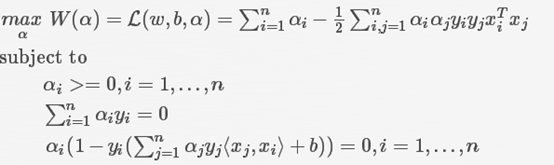
非常有趣的是,w被消掉了,可以通过α和b就可以直接使用到分类器中。并且都不需要考虑线性问题,可以用于解非线性的情况。
另外,需要注意到的是,前一幅图中的不等式,在这幅图中(最后一个公式,α乘以括号一串那个公式)变成了等式。特别注意的是,由于α是要求大于等于0,而后面那一串是要求小于等于0,因此为了满足这个等式,必须是α等于0或是后面括号内的结果等于0。
根据这个性质,会有一个非常重要的结论:SVM训练过程中,只需要拿在支持向量进行训练即可。支持向量,即括号内的等式等于0的。
可以这么考虑,当点远离这个边界,可以很明确的被分类到某处,此时明显xiwT+b远大于1,则为了满足拉格朗日的条件,必须是对应的α等于0。而看到上面拉格朗日的式子,如果α等于0,则整个式子都是0,因此可以不用考虑这个点。
当点在附近时,xiwT+b约等于1,此时,就需要对这个点再次训练其对应的α和b,因此这样的边界上的点,也就称为支持向量。
三、处理异常点
如下图的w点,就是一个异常点,会导致无法找到合适的超平面:

为了解决这个问题,引入了一个叫做松弛变量(slack variable)ξ的概念。公式变成了xiwT+b⩾1-ξi。对于拉格朗日乘子,主要是对α的限定变化了,如下:
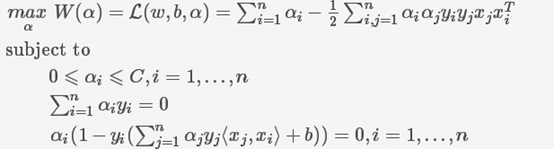
这个C越大,表示对异常的情况容忍度越大。C太小会限制α。
四、求解α——SMO法
John Platt发布了一个称为SMO的强大算法,用于训练SVM。SMO表示序列最小优化(Sequential Minimal Optimization)。这个大神在1998年写了一篇论文,讲述这个内容 ,《Sequential-Minimal-Optimization---A-Fast-Algorithm-for-Training-Support-Vector-Machines》,后面又有一个大神对其进行了改进和补充,写了《Improvements to Platt’s SMO Algorithm for SVM Classifier》,这两篇全英文的论文,后面准备找时间研究一下。
SMO的主要思想是每次取一对αi和αj,调整这两个值,迭代求解,过程如下:
1)初始化α为0;
2)在每次迭代中 (小于等于最大迭代数),
- 找到第一个不满足KKT条件的训练数据,对应的αi
- 在其它不满足KKT条件的训练数据中,找到误差最大的x,对应的index的αj
- αi和αj组成了一对,根据约束条件调整αi,αj
这里提到的KKT条件,即拉格朗日乘子中的约束条件。
这里可以调整的点,包括:
(1)yw≤1但是αi<C;(2)yw≥1但是αi>0;(3)yw≤1但是αi=0或αi=C。如下图所示:
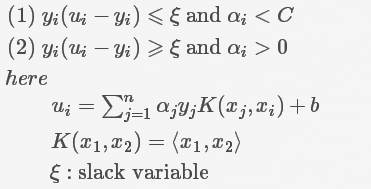
当迭代完一次后,会发现若干不满足条件且可以调整的点,这个时候SMO采取的策略是选择这10个中的两个α出来,假设为α1,α2,这里先给出结论,调整方式如下:
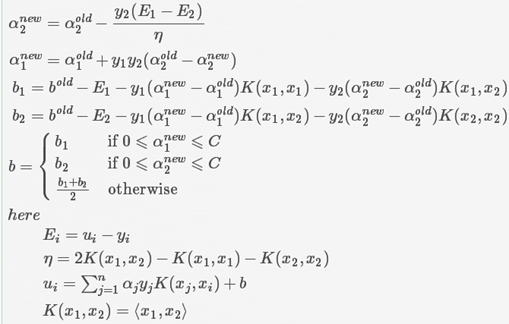
上图中的E,表示这个点的预测的误差。另外,因为所有对应的α*y的和是0,因此调整前后要求满足:
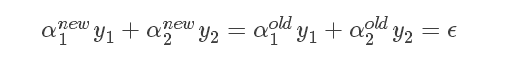
下面是推导过程。【这个问题我想了好久】
引用一段一个大神博客里的分析,来证明上面的公式。
假设我们来求α2。观察上面那个等式,y1,y2是标签,要么1要么-1。而两个α>=0。所以新的α是有范围的。假设现在y1=y2=1,那么αnew1+αnew2=αold1+αold2=ϵ
因为αnew1是在0-C之间,所以假设αnew1=0,那么αnew2可以取到最大值为ϵ,也就是αold1+αold2。而αnew2又不能大于C,所以其最大取值为min(C,αold1+αold2)。同理如果αnew1=C,那么αnew2可以取到最小值为ϵ−C,也就是αold1+αold2−C,而αnew2最小不能小于0,所以αnew2的下限值就为max(0,αold1+αold2−C)。这是相等取1。
当y1=y2=-1,同理,−αnew1−αnew2=−αold1−αold2=ϵ两边乘以-1,就是αnew1+αnew2=αold1+αold2=−ϵ,因为ϵ就是一个字母,用ϵ代替−ϵ,接下来的讨论过程一模一样,从而属于同类别的时候αnew2上下限就有了。同理去计算下不同类(1,-1)的时候的上下限。最终也能得到一个类似的结果,最终α的范围如下:
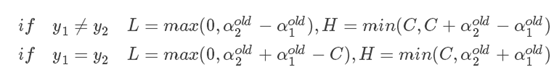
下面要求解α,把含有α1,α2都单独拿出来,其他的作为一堆,就变成下面这样:
W(α)=1/2K11α12+1/2K22α22+y1y2K12α1α2+y1α1v1+y2α2v2−α1−α2+W(α3...αn),v是一个与α1,α2,y1,y2有关的长式子,K是<x1∗x2>内积。可以看到后面一堆与α1,α2就没有关系。又因为有上面那个old、new的α的等式,可以消去α1new,而两个old又是上一次迭代结果,是已知数,故就变成了α2 new的式子。在令W对α2 new的导数为0,可以求出α2 new,进而求出α1 new。
这个计算过程太复杂,不详细描写。这里算出来的α,还需要满足上面的最大值和最小值的限制条件,超过最大值则令其为最大值,低于最小值则令其为最小值。
求出α后,可以根据w的公式,直接求出w。再带回到上面的带b的等式yi(w∗x+b)−1=0,可以求出b。但是由于一次性更新了两个α,对应的会求出两个b的值,要选择哪个b,规则是就是变换后的哪个α在0~C之间,也就是在分界线的边界上,也就是属于支持向量了,那么谁就准,就选那个α带入求出的b的值。
【推导结束】
接下来,剩下的就是循环,再次选择两个α,看是否需要更新(如果不满足KKT条件),不需要就重新选α,需要就更新α。一直到程序循环很多次(通常是用户设定的次数),都没有选择到两个不满足KKT条件的点,也就是所有的点都满足KKT了,那么就大功告成了。
改进:
当随机选取α,到后期时,由于大部分α已经被优化,剩下有问题的那些α很可能一直没有随机到,这样会浪费时间在不断的选择α中。因此,有了启发思想如下:
上一次的一些点的α在0-C之间,也就是这些点不满足条件需要调整,那么一次循环后,选中的α调整了一点,在下一次中,因为每一次的调整比较不可能完全,这些点还是更有可能不满足条件。而那些在上一次本身满足条件的点,那么在下一次后更有可能满足条件的。
所以在启发式的寻找α过程中,并不是遍历所有的点的α,而是遍历那些在0~C之间的α,而0~C反应到点上就是那些属于边界之间的点。当某次遍历在0~C之间找不到α了,那么再去整体遍历一次,这样就又会出现属于边界之间α了,然后再去遍历这些α,如此循环。
那么在遍历属于边界之间α的时候,因为是需要选两个α的,第一个可以随便选,第二个用一个启发式的思想,第1个α选择后,其对应的点与实际标签有一个误差,属于边界之间α的,所以每个点都会有一个自己的误差,这个时候选择剩下的点与第一个α点产生误差之差最大的那个点。
五、非线性分类
非线性分类,由于引入了拉格朗日,变成非常简单,只需要把上面求解α、b的公式中,对应的K函数,换成相应的非线性的核函数即可,常用的有高斯核函数,又称径向基函数(radial basis function)。
——written by linhxx
更多最新文章,欢迎关注微信公众号“决胜机器学习”,或扫描右边二维码。