排序算法——归并排序

归并排序的属性

 时间复杂度 O(n log n)空间复杂度 O（n)稳定性 稳定发明者 约翰·冯·诺伊曼 （就是那个计算机冯·诺伊曼体系的人）

归并排序是建立在归并操作上的一种有效的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

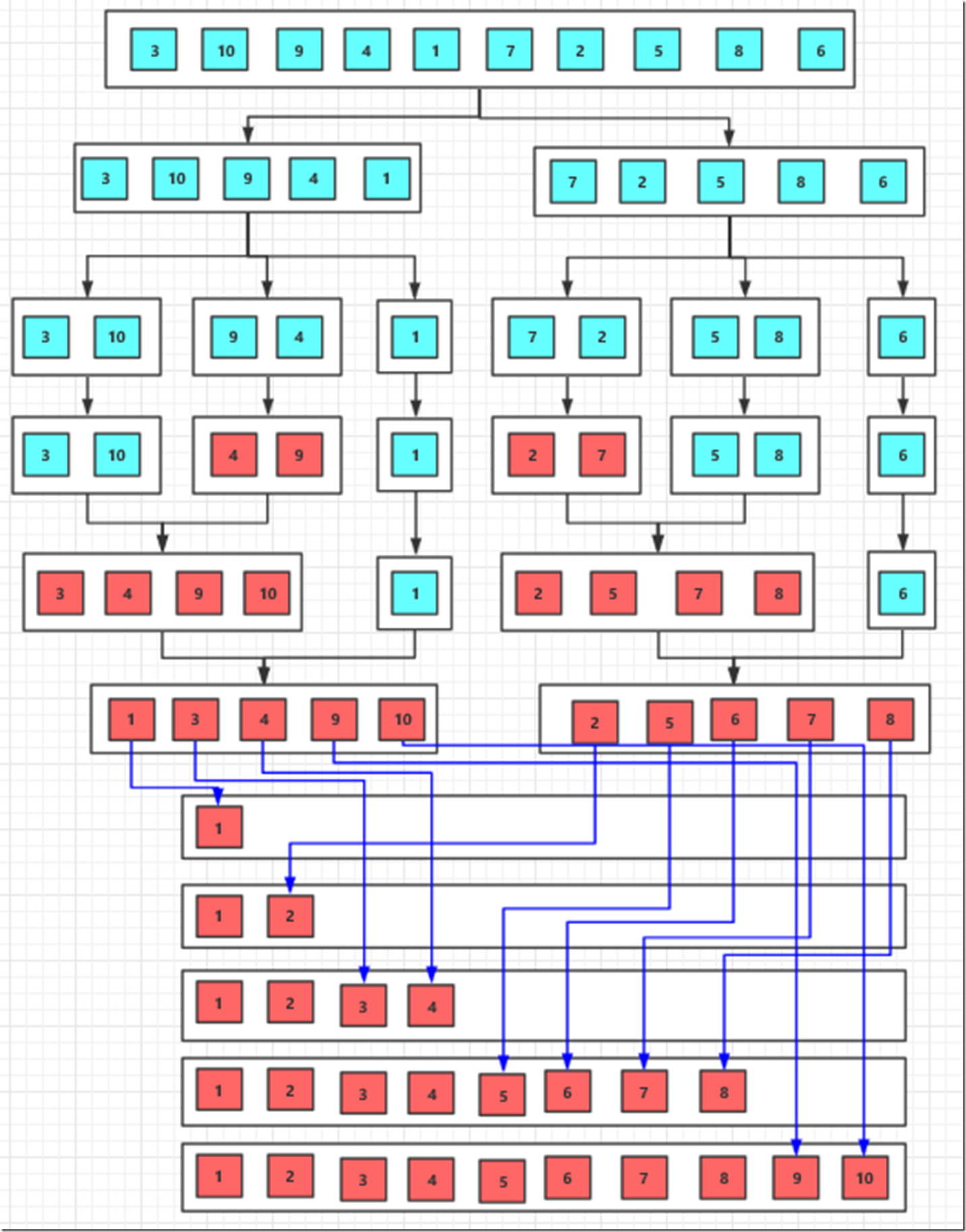
归并排序的图解

数组中使用归并排序

/**
*归并排序【数组】 
**/ 

#include <cstdio>
#include <cstdlib> 
#include <iostream>
#include <algorithm>

using namespace std;

//需要排序的数组 
int result[10]={3,10,9,4,1,7,2,5,8,6};
int flag=0;

//打印数组中的所有元素 
void print_arr()
{
    for(int i=0; i<10; i++)
        cout<<result[i]<<" ";
    cout<<endl;
}

//将两个已经排序的数组合并为一个新的已经排序的数组 
void merge(int start, int medium, int end)
{
    //第一个已经排序的数组，从start到medium
    int arr1_start = start;
    int arr1_end = medium;
    //第二个已经排序的数组，从medium+1到end
    int arr2_start = medium+1;
    int arr2_end = end;
    
    //临时数组保存最后的结果
    int temp[10],i=start;
    while(i != end+1)
    {
        if(arr1_start != medium+1 && (arr2_start == end+1 || result[arr1_start] < result[arr2_start]))
        {
            temp[i] = result[arr1_start];
            arr1_start++;
            i++;
        }
        else
        {
            temp[i] = result[arr2_start];
            arr2_start++;
            i++;
        }
    }
    
    //把临时存放的结果放到最终的结果数组中去 
    for(int j=start;j<=end;j++)
    {
        result[j] = temp[j];
    }
    
    flag++;
    cout<<"第"<<flag<<"次合并"<<endl; 
    print_arr();
}

//递归分解 
void merge_sort(int start,int end)
{
    //不能分解且只有一个元素 
    if(start == end){
        return;
    }
    
    //只有两个元素直接合并 
    if(start + 1 == end){
        merge(start,start,end);
        return;
    }
    
    int sum = end - start + 1;
    //分解成两组 
    merge_sort(start,sum/2+start-1);
    merge_sort(sum/2+start,end);
    //合并
    merge(start,sum/2+start-1,end);
}

int main() 
{
    print_arr();
    merge_sort(0,9);
    print_arr();
    return 0;
}

链表的归并

public class MergetSortList {

    public static  ListNode sortList(ListNode head) {
        if(head == null || head.next == null) return head;
        ListNode slow = head;
        ListNode fast = head;
        //用快慢指针找到中间节点
        while(fast.next != null && fast.next.next != null){
            slow = slow.next;
            fast = fast.next.next;
        }
        ListNode list2 = slow.next;
        slow.next = null;
        head = sortList(head);
        list2 = sortList(list2);
        return merge(head, list2);
    }

    private static ListNode merge(ListNode list1, ListNode list2) {
        if(list1 == null) return list2;
        if(list2 == null) return list1;
        ListNode newHead = new ListNode(0);//链表头不存储实际数据
        ListNode last = newHead;
        last = newHead;
        //连接每个节点，只更换指针，因此空间复杂度为O(1)
        while(list1 != null && list2 != null){
            if(list1.val < list2.val){
                last.next = list1;
                list1 = list1.next;
            }else{
                last.next = list2;
                list2 = list2.next;
            }
            last = last.next;
        }
        //最后剩余的部分，直接连接起来即可
        if(list1 != null) last.next = list1;
        else if(list2 != null) last.next = list2;
        return newHead.next;
    }

    public static void main(String[] args) {
        ListNode l1 = new ListNode(8);
        ListNode l2 = new ListNode(7);
        ListNode l3 = new ListNode(6);
        ListNode l4 = new ListNode(5);
        ListNode l5 = new ListNode(4);
        ListNode l6 = new ListNode(3);

        l1.next = l2;
        l2.next = l3;
        l3.next = l4;
        l4.next = l5;
        l5.next = l6;

        l1 = sortList(l1);

        while(l1 != null){
            System.out.print(l1.val + " ");
            l1 = l1.next;
        }
    }
}

归并排序的使用

对于归并排序来说有一点是，这个排序算法是稳定的，也就是相同的两个数不会位置不会进行交换。

所以当需要稳定排序的时候就可以使用归并。

还有就是当我们看见有两个已经排序好的数据结构，我们可以考虑利用这种归并的思想去解决这样的问题。