LeetCode152. 乘积最大子数组

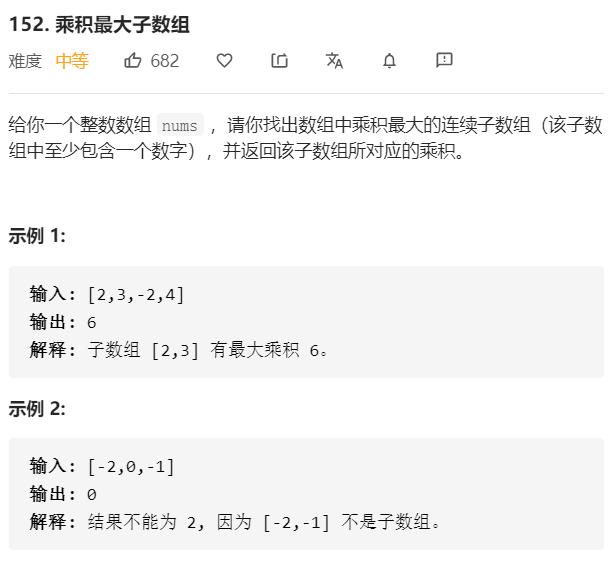
要求乘积最大的子数组（子数组一定都是连续的），可以暴力枚举子数组起点和终点，求和。但是肯定超时。

如果用动态规划，则只需要一遍扫描就可以得出结果。

可以用maxProduct[i]表示以i结尾的最大的子数组乘积。

如果所有nums[i]都是正数，则maxProduct[i]就是max(nums[i], maxProduct[i - 1] * nums[i])，
也就是当前数和以i - 1结尾的最大子数组乘积和当前数的乘积的较大值。

但是在这题里，nums[i]有可能是负数，众所周知负负得正，所以有可能前面某个子数组的乘积非常的“负”且当前的nums[i]也是一个负数，
以至于之前的那个负的子数组的积和nums[i]的乘积反而是最大的。

因此我们不仅需要一个maxProduct数组记录以当前位置i结尾的最大子数组的积，还需要一个minProduct数组记录以当前位置i结尾的最小子数组的积。

对于每一个maxProduct[i],它的值应该是nums[i], maxProduct[i - 1] * nums[i], minProduct[i - 1] * nums[i]三者中最大的，
对于每一个minProduct[i],它的值是三者中最小的。

我们只需要一遍扫描更新所有的maxProduct和minProduct。

最终答案就是maxProduct数组中的最大值。

代码如下：

class Solution {
public:
    int maxProduct(vector<int>& nums) {
        int size = nums.size();
        vector<int> maxProduct(size), minProduct(size);
        maxProduct[0] = nums[0], minProduct[0] = nums[0];
        for(int i = 1; i < size; ++i) {
            maxProduct[i] = max(nums[i], max(maxProduct[i - 1] * nums[i], minProduct[i - 1] * nums[i]));            //这一行和下一行对调位置也行，只要更新了maxProduct和minProduct就好
            minProduct[i] = min(nums[i], min(maxProduct[i - 1] * nums[i], minProduct[i - 1] * nums[i]));
        }
        return *max_element(maxProduct.begin(), maxProduct.end());
    }
};